Теоретические основы математического моделирования в машиностроении

Без преувеличения можно отметить, что определяющая роль в построении математических моделей технических систем принадлежит математическим методам при рациональном их применении. Наряду с аналитическими методами анализа непрерывных процессов, дифференциальным и интегральным исчислением, широкое применение находят методы дискретной математики (теории множеств, графов и др.), на которых базируются теоретические основы систем автоматизированного проектирования (САПР), автоматизированные системы управления технологическими процессами (АСУ ТП), автоматизированные системы управления производством (АСУП) и сопутствующих компонент, включающих решение важных научно-технических задач. Вопросы идентификации технических и организационных систем и их составляющих, построение физико-статистических моделей процессов при наличии случайных параметров, протекающих в технологических системах, их имитационное моделирование решаются на базе теории вероятностей, теории случайных функций, математической статистики и теории планирования эксперимента.

Важным в процессе математического моделирования при реализации его результатов на практике, особенно при условии их многовариантности, что характерно для технологии машиностроения, является знание и правильное применение теории принятия решений, базирующейся на теории игр и теории массового обслуживания.

Большую роль в моделировании и проектировании технологических процессов производства играет описательный способ задания множеств оборудования, инструмента, операций, поверхностей, физических процессов и др. Он связывает учение о множествах с учением о высказываниях, составляющее часть математической логики, которая обеспечивает математически строгое логическое описание, синтез и рациональный выбор как самого технологического процесса, так и его компонент.

Практически на всех этапах математического моделирования приходится оперировать с матрицами, особенно в системах построения физико-статистических моделей методами корреляционно-регрессионного анализа, планирования эксперимента и нейросетевого моделирования.

Что же представляет собой математический аппарат инженера?

Математический аппарат инженера определяется как взаимосвязанная совокупность языка, методов математики и моделей, ориентированная на решение инженерных задач.

В формальный язык математики и ее разделов входят системы символов, обозначающие математические объекты и переменные, а также операции над объектами и отношения между ними.

Так, различные типы геометрии классифицированы Феликсом Клейном в соответствии с теми свойствами фигур, которые остаются неизменными, когда они подвергаются разнообразным группам преобразований.

Эвклидова геометрия изучает такие объекты как углы, которые сохраняются при повороте, переносе, сжатии, растяжении. В афинной геометрии отношение коллинеарных отрезков постоянно 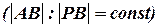. В проективной геометрии инвариантно перекрестное отношение коллинеарных отрезков . Топология изучает свойства, сохраняющиеся при изгибах, сжатиях, растяжениях, кручении. Порядок следования точек при таких деформациях сохраняется. В теории точечных множеств рассеянные точки сохраняют нумерацию , совпадающую с нумерацией точек исходной фигуры. Теория точечных множеств в широком смысле может быть представлена как изучение свойств, сохраняющихся при взаимно однозначных преобразованиях.

В соответствии с этим в технических задачах может быть использован различный формальный язык математики. Так, при моделировании процессов термомеханической обработки при рассмотрении упругости и пластичности обрабатываемого материала целесообразно использовать Эвклидову и аффинную геометрию, при описании пластичности и вязкости среды– переходить от афинной геометрии к топологии. В процессах ионно-лучевой обработки рационально использовать проективную геометрию при лучевых процессах, а теорию точечных множеств – при воздействии частицами.

Рис. Эвклидова геометрия, включающая:

а – параллельный перенос; б – поворот; в – равномерное сжатие и растяжение

Поиск по сайту: