Классификация методов оптимизации

Методы оптимизации исторически развивались независимо с использованием различных концепций, математических аппаратов и т.д., что объясняет определённую сложность их классификации. Рассмотрим классификацию методов оптимизации в трактовке работы которая, хотя и носит условный характер, даёт возможность ознакомиться с их особенностями и областями применения.

Исходя из возмож­ности нескольких под­ходов к классификации, следует различать мето­ды определения экстре­мума функции и функционала (рис.). Являясь частным случа­ем функционала, функ­ция отличается более простыми методами отыскания экстремума.

Современная прак­тика оптимизации производственных про­цессов требует приме­нения как аналити­ческих, так и численных методов поиска экстремума. Преимущество аналитических методов заключается в возможности определения качественной картины поведения опти­мальной системы при изменении её параметров и структуры. Применение численных методов обеспе­чивает получение конкрет­ных числовых значений параметров управления производственным процес­сом.

Особое место занимают человеко-машинные методы оптимизации, использующие возможности работы оператора в режиме диалога с ЭВМ. Это даёт возможность повторять вычисления при разных условиях, использовать аналитические методы, представленные в виде стандартных программных блоков и, что самое важное, оперативно включать в процедуру отыскания оптимального решения интеллектуальные способности человека. Весьма важно, что при таком способе оптимизации исходный критерий оптимальности может быть нестрого математически формализован в виде функции или функционала. Так, он может состоять из нескольких положений, сформулированных достаточно чётко на словесном, содержательном уровне, что при наличии диалога человек - машина вполне допустимо.

Методы отыскания экстремума функции получили широкое развитие из-за вычислительных трудностей решения алгебраических уравнений вида

, j =1,2,…n,

особенно при наличии ограничений на переменные .

Увеличение числа переменных и ограничений на них ведет к резкому возрастанию сложности решения уравнений. В связи с этим широкое распространение получили прямые методы отыскания экстремума функции, методы линейного и нелинейного программирования, дискретные принципы максимума и динамическое программирование. Методы динамического программирования и принципа максимума с успехом применяются для отыскания экстремума функционала и функции. Прямые методы вариационного исчисления (методы Ритца, Эйлера и др.), как дискретный вариант уравнения Эйлера, сводят задачу отыскания экстремума функционала к экстремуму функции. Методы поиска экстремума функционала включают в себя как классические (методы Эйлера-Лагранжа-Гамильтона), так прямые и различные специальные методы, а заканчиваются динамическим программированием и принципом максимума.

Во многих областях практики, в том числе и в машиностроении, возникают задачи оптимизации применяемых решений, имеющих следующие характерные черты:

· показатель эффективности представляет собой линейную функцию от элементов решения ;

· ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Такие задачи составляют круг задач линейного программирования.

Вопросы для самопроверки

1. Какова роль системного подхода в решении задач оптимизации технических систем?

2. Чем занимается прогрматика как наука?

3. Дайте определение семиотики и математической лингвистики.

4. Приведите примеры наиболее распространенных видов критериев оптимизации и областей их применения.

5. Какие задачи составляют круг задач линейного программирования?

Рекомендуемая литература.

1. Аверченков, В.И. Основы математического моделирования технических систем: учеб. пособие / В.И. Аверченков, В.П. Федоров., М.Л. Хейфец – Брянск: Изд-во БГТУ, 2004.

2. Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. – М.:Советское радио, 1972.

3. Вентцель, Е.С. Исследование операций / Е.С. Вентцель. – М.:Наука, Гл. ред. физ.-мат. лит., 1998.

Интеллектуальные «в малом» не удовлетворяют перечисленным принципам, но используют при функционировании знания (можно в виде правил) как средство преодоления неопределенности входной информации, описания управляемого объекта или его поведения.

При проектировании ИСУ наибольшее распространение получили методы ИУ, относящиеся к следующим четырем классам:

· экспертные системы;

· нечеткие регуляторы;

· нейронные сети;

· генетические алгоритмы.

В случае четких множеств традиционный способ представления элемента множества состоит в применении характеристической функции 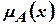. Для четких множеств имеем:

В нечетких множествах элемент может частично принадлежать любому множеству.

Степень принадлежности элемента множеству определяется функцией принадлежности , которая представляет собой обобщение характеристической функции. Ее значения являются рациональными числами из интервала . Причем 0 означает отсутствие принадлежности, а 1 – полную принадлежность к множеству .

Конкретное значение функции принадлежности называется степенью, или коэффициентом принадлежности. Степень принадлежности может быть определена в виде функциональной зависимости или дискретно – путем задания конечной последовательности значений в виде:

Теория нечетких множеств допускает, помимо переменных цифрового типа, существование лингвистических переменных с приписываемыми им значениями.

Для нечетких множеств, являющихся обобщением обычных множеств, существует ряд математических операций, которые являются обобщением аналогичных операций, выполняемых на четких множествах. Среди прочих, к ним относятся следующие:

1. Логическая сумма множеств .

.

2. Логическое произведение множеств .

.

Здесь знаки и обозначают соответственно операторы и .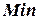

3. Отрицание множества

.

Отрицание нечеткого множества в отличие от обычных четких множеств дает непустое множество, состоящее из элементов, функции принадлежности которых также определены на интервале .

4. Равенство нечетких множеств и возможно, когда для всех элементов обоих множеств выполняется условие .

5. Операции концентрации

.

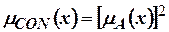Часто выполняется при действиях с лингвистической переменной, в которых она отождествляется с интенсификатором «очень».

6. Операция растяжения

.

Лингвистическое значение этой операции формулируется как «примерно» или «приблизительно».

7. Ограниченная сумма , разность и произведение двух нечетких множеств определяются соответственно выражениями:

, , .

8. Нормализация нечеткого множества 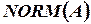определяется соотношением

.

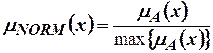Нечеткое множество считается подмножеством нечеткого множества 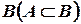, если для всех элементов выполняется неравенство .

Свойства ассоциативности, коммутативности и дистрибутивности операций, определенных на нечетких множествах, понимаются следующим образом:

· ассоциативность: ;

· коммутативность: (за исключением ограниченной разности);

· дистрибутивность: , где операторы и обозначают любую определенную выше операцию на нечетких множествах.

Для нечетких множеств корректны следующие выражения:

Æ;

,

т.е. в отличие от обычных множеств, логическое произведение нечеткого множества и его отрицания не обязательно образуют пустое множество, а их логическая сумма не обязательно образует полное множество .

Важным для практики является вопрос о степени нечеткости нечетких множеств. Для ее определения введено понятие меры нечеткости, сводящейся к измерению уровня различия между множеством и его отрицанием .

В соответствии с мерой Р. Егера степень нечеткости множества в метрике , обозначаемая , определяется по формуле:

,

где 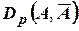– мера расстояния между множествами и , содержащими по 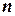элементов.

Значения и соответствуют метрикам Хемминга и Евклида, и искомые меры расстояния определяются по формулам:

; .

Вопросы для самопроверки.

1. Что такое интеллектуальная система управления и какой она имеет необходимый признак?

2. Охарактеризуйте четыре метода интеллектуального управления.

3. Что такое функция принадлежности и коэффициент принадлежности в теории нечетких множеств?

4. Дайте определение следующих математических операций для нечетких множеств: логическая сумма; логическое произведение; отрицание множества; равенство нечетких множеств; операции концентрации и растяжения; ограниченные сумма, разность и произведение; нормализация нечеткого множества.

5. Свойства (ассоциативность, коммутативность, дистрибутивность) нечетких множеств.

6. Как определяется степень нечеткости (мера Егера) нечетких множеств?

Рекомендуемая литература

1. Аверченков, В.И. Основы математического моделирования технических систем: учеб. пособие / В.И. Аверченков, В.П. Федоров., М.Л. Хейфец – Брянск: Изд-во БГТУ, 2004.

Лекция 9. (Окончание раздела 6) «Применение нейросетевого моделирования и генетических алгоритмов в моделировании технических систем» (1 час)

План лекции:

9.1. Элементы нейросетевого моделирования процессов в технических объектах и системах.

9.2. Генетические алгоритмы и их применение в моделировании технических систем.

Поиск по сайту: