Изложить алгоритм Флойда для нахождения кратчайших путей в графе и перечислить аспекты применения алгоритма

Шаг 0. Определяем начальную матрицу расстояний D0 и матрицу последовательности узлов S0. диагональные элементы обеих матриц помечаются знаком «-», так как эти элементы в вычислениях не участвуют. Полагаем k =1птак как эти элементы в вычислениях не участвуют. Основной шаг k:

Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dij матрицы Dk-1. если выполняется неравенство 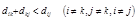,то выполняются следующие действия:а) создаем матрицу Dk путем замены в матрице Dk-1 элемента dij на сумму ;

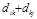б) создаем матрицу Sk путем замены элемента sj на k.

1)После реализации n шагов алгоритма можно определить кратчайший путь по матрицам Dn и Sn между узлами i и j, пользуясь следующими правилами: Расстояние между i и j равно dij в матрице Dn.2)Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn.

Пусть sij = k, тогда имеем путь i → j → k.

Если далее sik = k и skj = k, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу j и от узла k к узлу j.

Поиск по сайту: