АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Изложить алгоритм нахождения оптимального решения ЗЛП симплексным методом

Читайте также:
  1. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  2. III. Определение оптимального уровня денежных средств.
  3. MathCad: способы решения системы уравнений.
  4. SALVATOR - это переход физического явления в семантико-нейронный алгоритм (инструкцию) освобождения человека от негативных последствий этого явления.
  5. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  6. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  7. Алгоритм
  8. Алгоритм
  9. Алгоритм
  10. Алгоритм
  11. Алгоритм 65 «Кровотечение в послеродовом периоде»
  12. Алгоритм 72 «Ожоги и травмы глаза, века, конъюнктивы»

Алгоритм нахождения оптимального решения:

Ø Считаем, что в симплексной таблице найдено опорное решение. Просматриваем коэффициенты строки функции таблицы. Если все они неотрицательные, то оптимальное решение достигнуто. В этом решении все не базисные неизвестные =0, а базисные – свободным членам таблицы.

Ø Если среди коэффициентов строки функции имеются отрицательные, то выбираем среди них наибольший по абсолютной величине и столбец в котором находится этот коэффициент, берем за разрешающий

Ø Разрешающую строку находим по наименьшему симплексному отношению

Ø С найденным разрешающим элементом рассчитываем новую таблицу по следующим правилам:

Ø Разрешающий элемент заменяем обратно.

Ø Все элементы разрешающей строки делим на разрешающее число.

Ø Все элементы разрешающего столбца делим на разрешающее число с противоположным знаком.

Ø Оставшиеся элементы вычисляем по правилу прямоугольника:

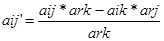,где ark-разрешающий элемент.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)