Изложить алгоритм нахождения опорного решения симплексным методом

Для нахождения оптимального решения используется следующий алгоритм:

1)Выбирают разрешающий столбец ар из условия: оценка Δ<0 и хотя бы один элемент аip>0. 2) Выбирают q-ю разрешающую строку из условия 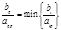для аip>0.

3) Приводят пересчет элементов разрешающей q–й строки по формуле (k=0,1, …, n)

4) Вычисляют элементы всех остальных строк (при 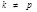)по формуле (i=0,1, …, q-1, q+1,…,r).

26. Перечислить симплексные преобразования для улучшения плана ЗЛП.

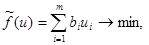(4)

(5)

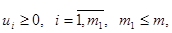(6)

произвольного знака при .

Задача (4)-(6), двойственная к задаче (1)-(3), строится по следующим правилам:

1) упорядочивается запись исходной задачи, т.е. если целевая функция задачи максимизируется, то ограничения неравенства должны быть вида 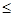, если минимизируется – то вида 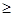. Выполнение этих условий достигается умножением соответствующих ограничений на (-1);

2) если исходная задача является задачей максимизации, то двойственная будет задачей минимизации. При этом вектор, образованный из коэффициентов при неизвестных целевой функции исходной задачи, совпадает с вектором констант в правых частях системы ограничений двойственной задачи, и, наоборот, коэффициентами при неизвестных целевой функции двойственной задачи являются соответствующие правые части системы ограничений исходной задачи;

3) каждой переменной двойственной задачи соответствует i-е ограничение исходной задачи, и, наоборот, каждой переменной 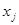прямой задачи соответствует j-е ограничение двойственной задачи;

4) матрица из коэффициентов при неизвестных двойственной задачи образуется транспонированием матрицы 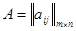, составленной из коэффициентов при неизвестных системы ограничений исходной задачи;

5) если на j-ю переменную исходной задачи наложено условие неотрицательности, то j-е ограничение двойственной задачи будет неравенством, в противном случае j-е ограничение будет равенством; аналогично связаны между собой ограничения исходной задачи и переменные двойственной.

Поиск по сайту: