Базовые теоремы

Теорема 1

Если P_m(n) - функция сложности, представленная полиномом порядка m относительно n, то P_m(n) = Q(n^m).

Доказательство

Так как полином

P_m(n) = a_mn ^m + a_m-1n ^m-1 +... + a₀

есть функция сложности алгоритма, то он монотонно не убывает с ростом n для n>0. Отсюда следует, что a_m>0. Требуется доказать, что $ c₁, c₂ >0 и такое n₀, что для любого n > n₀ будут выполняться неравенства:

c₁ n^m £ P_m(n) £ c₂ n^m. (1)

Разделим оба неравенства на n^m:

c₁ £ a_m + R(n) £ c₂ , (2)

где

R(n) = a_m-1n^-1 + a_m-2n^-2 +... + a₀n^-m.

Т.к. , то существует такое n₀, что . Выберем 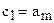, а . Тогда для любого n > n₀ неравенства (2) и, следовательно, (1) будут выполнены.

Теорема 2

(3)

Доказательство

Сумма слева есть арифметическая прогрессия, отсюда

.

Тогда справедливость (3) прямо следует из теоремы 1.

Теорема 3

. (4)

Доказательство

Доказывется также, как и теорема 2. Известно, что [2]

.

Из теоремы 1 следует справедливость (4).

Теорема 4

. (5)

Доказательство

¨Известно, что сумма слева связана с многочленами и числами Бернулли следующим соотношением:

. (6)

где B_m(n) - многочлен Бернулли:

, (7)

а b_k - числа Бернулли. Это рациональные числа, приведем первые из них: _b0 = 1, b₁ = -1/2, b₂ = 1/6, b₃ = 0, b₄ = -1/30.

Из (6) и (7) следует, что

.

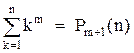При этом коэффициент первого (старшего) члена суммы положителен:

.

Отсюда следует справедливость теоремы.

¨

Полезное равенство:

.

Доказать предлагается самостоятельно.

Поиск по сайту: