Основной закон радиоактивного распада. Для отдельно взятого ядра радиоактивного атома невозможно предсказать время, в течение которого оно распадется

Для отдельно взятого ядра радиоактивного атома невозможно предсказать время, в течение которого оно распадется, можно лишь сделать заключение о вероятности данного события. Если же имеется большая совокупность ядер, то легко получить статистический закон, выражающий зависимость числа нераспавшихся ядер от времени. Он устанавливается на основании следующих соображений.

Будем считать, что за малый промежуток времени dt распадется число ядер dN. Очевидно, это число пропорционально промежутку времени dt и общему числу нераспавшихся к этому моменту радио­активных ядер N. Тогда дифференциалъное уравнение, описывающее процесс распада, запишем в виде:

dN = - l N dt. (2.1)

Знак минус указывает на убыль числа нераспавшихся ядер со временем, а коэффициент l зависит от вида ядер и называется поcтоянной распада. Введем начальное условие для этого уравнения, обозначив число атомов в начальный момент времени через N₀ (N = N₀ при t = 0). Решение дифференциального уравнения (2.I) с учетом введенного начального условия приводит к результату:

N = N₀ е ^{- lt}. (2.2)

Таким образом, закон радиоактивного распада получен - число нераспавшихся атомов убывает со временем экспоненциально. Скорость распада определяется видом атомов - входящей в по­казатель экспоненты постоянной распада. На практике вместо постоянной распада используют однозначно связанную с ней величину – период полураспада - то время, за которое распа­дается половина радиоактивных ядер (остается их число, равное N₀/2). Период полураспада может быть определен из графи­ческой зависимости N(t), представленной на рис. 2.5.

Установим аналитическую связь между постоянной распада l и периодом полураспада Т. Для этого подставим в уравнение (2.2) t = Т,
тогда N₀/2 = N₀ е ^{- lТ}.

Преобразуя полученное выражение, получим: 2 = е^{- lТ}.

Окончательно: .

Отметим, что постоянная распада l измеряется в единицах, обрат­ных времени, а период полураспада определяют в секундах, часах, годах и т.д.

Кроме введенных параметров l и Т радионуклиды характеризуют иногда средним временемжизни t -тем промежутком времени, за который число нераспавшихся ядер убывает в е раз. Среднее время жизни также определяется через l или Т. Подставив в уравнение (2.2) t = t и N = N₀/е, получим:

t = .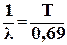

Если радионуклиды находятся в организме, то уменьшение в нем их количества определяется не только радиоактивным распадом по закону (2.2), но и биологическим выведением. Количественно, процессы выведения характеризуют постоянной биологического выведения l_Б или, чаще, периодом биологического полувыведения Т_Б -это время, за которое количество радионуклидов в организме (или органе) уменьшается вдвое только вследствие выведения. Очевидно, что Т_Б = ln2/l_Б.

Дифференциальное уравнение (2.1) радиоактивного распада для описания исчезновения выводящихся из организма радионуклидов, принимает вид:

dN = -(l_Р + l_Б) N dt или dN = - l _эф N dt, (2.3)

где dN -по-прежнему убыль нераспавшихся ядер за время dt,
l _эф = l_Р + l_Б – эффективная постоянная, измеряемая в единицах, обратных времени (с^-1, сут^-1 и др.), l_Р - постоянная радиоактивного распада, обозначавшаяся ранее символом l.

Эффективный период биологического полувыведения Т_эф – это время половинного исчезновения радионуклидов за счет указанных двух процессов – распада и выведения. Его связь с Т_Б и Т_р (периодом полураспада, обозначавшимся ранее символом Т) легко получить из соотношения:

l _эф =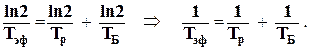

Следовательно:

Т_эф = ( 2.4)

Если в органе содержатся короткоживущие радионуклиды (например, ¹³¹I, для которого Т_р = 8 суток, Т_Б = 138 суток, т.е. Т_р << Т_Б), то время их исчезновения из организма практически определяется периодом полураспада.

Когда, наоборот, Т_р >> Т_Б, то время очистки организма от радионуклидов определяется практически только процессами выведения. Это наблюдается, например, для ¹³⁷Сs, у которого период полураспада 30 лет, а период полувыведения около 70 суток.

Большую опасность для организма создают инкорпорированные в нем радионуклиды с большими значениями Т_р и Т_Б. Например, ²³⁹Рu, который имеет период полураспада 24 тыс. лет и практически не выводится из организма.

Поиск по сайту: