Квадратичные функции и сопряженные направления

Ва­ж­ной иде­ей, ко­то­рая при­ве­ла к раз­ра­бот­ке ме­то­дов с вы­со­кой (почти нью­то­нов­ской) ско­ро­стью схо­ди­мо­сти без вычис­ле­ния вто­рых про­из­вод­ных, ока­за­лось ис­поль­зо­ва­ние вза­им­но со­пря­жен­ных на­пра­в­ле­ний по­ис­ка ми­ни­му­ма. Вначале мы рас­смо­т­рим этот под­ход при­ме­ни­тель­но к ми­ни­ми­за­ции ква­д­ра­тичных функ­ций, по­сколь­ку по­лу­чен­ные здесь ре­зуль­та­ты да­ют стро­гое те­о­ре­тичес­кое обо­с­но­ва­ние ме­то­да со­пря­жен­ных на­пра­в­ле­ний.

Два ве­к­то­ра u и v в N-мер­ном про­стран­с­т­ве на­зы­ва­ют­ся со­пря­жен­ны­ми от­но­си­тель­но сим­мет­ричной по­ло­жи­тель­но оп­ре­де­лен­ной ма­т­ри­цы A, ес­ли име­ет ме­с­то со­от­но­ше­ние

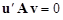. (13)

Лег­ко по­ка­зать, что ес­ли в N-мер­ном про­стран­с­т­ве най­де­но N вза­им­но со­пря­жен­ных (от­но­си­тель­но не­ко­то­рой ма­т­ри­цы A) ве­к­то­ров v₁, v₂, ¼, v_N, то они ли­ней­но не­за­ви­си­мы. От­сю­да вы­те­ка­ют два след­ст­вия:

1) В N-мер­ном про­стран­с­т­ве нель­зя по­стро­ить бо­лее N вза­им­но со­пря­жен­ных на­пра­в­ле­ний;

2) Со­пря­жен­ные ве­к­то­ры мо­гут слу­жить ба­зи­сом, т. е. лю­бое пе­ре­ме­ще­ние в N-мер­ном про­стран­с­т­ве мо­ж­но пред­ста­вить в ви­де сум­мы пе­ре­ме­ще­ний вдоль N вза­им­но со­пря­жен­ных на­пра­в­ле­ний.

Пусть F(x) – ква­д­ра­тичная функ­ция N пе­ре­мен­ных, пред­ста­в­лен­ных ве­к­то­ром x. Ис­поль­зуя ма­т­ричную за­пись, ее мо­ж­но в об­щем случае пред­ста­вить в ви­де

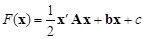, (14)

где A – сим­мет­ричная ма­т­ри­ца ко­эф­фи­ци­ен­тов ква­д­ра­тичных чле­нов, b – ве­к­тор ко­эф­фи­ци­ен­тов ли­ней­ных чле­нов, c – ска­ляр­ная по­сто­ян­ная. Диф­фе­рен­ци­руя (14) по x, по­лучим ве­к­тор гра­ди­ен­та:

. (15)

Ра­вен­ст­во гра­ди­ен­та ну­лю яв­ля­ет­ся ус­ло­ви­ем, оп­ре­де­ля­ю­щим ста­ци­о­нар­ную точку:

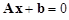. (16)

В за­ви­си­мо­сти от свойств ма­т­ри­цы A это мо­жет быть точка ми­ни­му­ма, ма­к­си­му­ма или се­д­ло­вая точка. В час­т­но­сти, ес­ли A яв­ля­ет­ся по­ло­жи­тель­но оп­ре­де­лен­ной, ре­ше­ние урав­не­ния (16) со­от­вет­ст­ву­ет точке ми­ни­му­ма.

Итак, бу­дем пред­по­ла­гать, что A – сим­мет­ричная по­ло­жи­тель­но оп­ре­де­лен­ная ма­т­ри­ца. Обоз­начим x*ра­ди­ус-ве­к­тор точки ми­ни­му­ма функ­ции (14). Очевид­но, x*удо­в­ле­тво­ря­ет урав­не­нию (16), т. е.

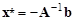. (17)

Та­ким об­ра­зом, точное по­ло­же­ние ми­ни­му­ма ква­д­ра­тичной функ­ции мо­жет быть най­де­но за один шаг пу­тем ре­ше­ния си­с­те­мы ли­ней­ных урав­не­ний (16). В этом смы­с­ле ми­ни­ми­за­ция функ­ции (14) не пред­ста­в­ля­ет про­б­ле­мы. Од­на­ко, дан­ная за­дача ин­те­ре­су­ет нас не са­ма по се­бе, а как мо­дель для по­стро­е­ния ал­го­рит­ма по­ис­ка ми­ни­му­ма функ­ции об­ще­го ви­да.

Возь­мем про­из­воль­ную началь­ную точку x₀ и вычис­лим в этой точке гра­ди­ент g₀:

g₀=Ax₀+b. (18)

По­сту­пая так же, как в ме­то­де ско­рей­ше­го спу­с­ка, про­ве­дем от точки x₀ од­но­мер­ный по­иск ми­ни­му­ма вдоль на­пра­в­ле­ния ан­ти­гра­ди­ен­та -g₀, т. е. най­дем точку x₁=x₀-a₀g₀, где a₀ – ко­эф­фи­ци­ент, со­от­вет­ст­ву­ю­щий рас­сто­я­нию от x₀ до x₁, вы­ра­жен­но­му в еди­ни­цах дли­ны ве­к­то­ра g₀ (см. урав­не­ние (9) в раз­де­ле 2.1.2). Значение a₀ оп­ре­де­ля­ет­ся из ус­ло­вия, что x₁ от­вечает ми­ни­му­му F(x) по на­пра­в­ле­нию g₀, т. е.

,
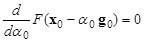от­ку­да с учетом (14) и (18) по­лучаем:

. (19)

Вычис­лим но­вый ве­к­тор гра­ди­ен­та в най­ден­ной точке x₁:

g₁=Ax₁+b=A·(x₀-a₀g₀)+b=g₀-a₀Ag₀ (20)

Ес­ли бы мы ре­ша­ли за­дачу с по­мо­щью ме­то­да ско­рей­ше­го спу­с­ка, да­лее сле­до­ва­ло бы про­ве­с­ти по­иск ми­ни­му­ма вдоль на­пра­в­ле­ния -g₁ и т. д. Вме­сто это­го на вто­ром ша­ге ис­поль­зу­ем на­пра­в­ле­ние по­ис­ка, со­пря­жен­ное к на­пра­в­ле­нию пер­во­го ша­га -g₀ от­но­си­тель­но ма­т­ри­цы A:

(x₂-x₁)¢Ag₀=0 (21)

(сравните (21) с урав­не­ни­ем (13)).

Урав­не­ние (21) фа­к­тичес­ки оп­ре­де­ля­ет (N-1)-мер­ное под­про­стран­с­т­во в про­стран­с­т­ве N‑мер­ных ве­к­то­ров x, так как удо­в­ле­тво­ря­ю­щие ему точки x₂ ле­жат в ги­пер­п­ло­ско­сти, про­хо­дя­щей через точку x₁ и ор­то­го­наль­ной к ве­к­то­ру Ag₀. За­ме­тим, что на­ша ко­нечная цель — точка ми­ни­му­ма x*— так­же ле­жит в этой ги­пер­п­ло­ско­сти. Дей­ст­ви­тель­но, под­ста­вив в (21) вме­сто x₂ вы­ра­же­ние (17), по­лучим:

(-A^-1b-x₁)¢Ag₀=-b¢A^-1Ag₀-x₁¢Ag₀=-(b+Ax₁)¢g₀=-g₁¢g₀.

Так как g₁ — ве­к­тор гра­ди­ен­та в точке ми­ни­му­ма, най­ден­ной при по­ис­ке вдоль на­пра­в­ле­ния g₀, то g₀ и g₁ вза­им­но ор­то­го­наль­ны (мы уже об­су­ж­да­ли это об­сто­я­тель­ст­во при рас­смо­т­ре­нии ме­то­да ско­рей­ше­го спу­с­ка — см. рис. 7), т. е. g₁¢g₀=0. Сле­до­ва­тель­но, точка x*удо­в­ле­тво­ря­ет урав­не­нию (21), и ее мо­ж­но до­с­тичь, не вы­хо­дя за пре­де­лы ги­пер­п­ло­ско­сти.

Сре­ди всех воз­мо­ж­ных на­пра­в­ле­ний по­ис­ка, ле­жа­щих в (N-1)-мер­ном под­про­стран­с­т­ве, вы­бе­рем наи­бо­лее бли­з­кое к g₁ — про­ек­цию p₁ гра­ди­ен­та на ги­пер­п­ло­скость (21). Бу­дем ис­кать ее в ви­де

p₁=g₁+b₀g₀, (22)

где b₀ – под­ле­жа­щий оп­ре­де­ле­нию чис­ло­вой ко­эф­фи­ци­ент. Так как p₁ ле­жит в ги­пер­п­ло­ско­сти (21), он дол­жен быть ор­то­го­наль­ным к Ag₀, т. е.

p₁¢Ag₀=(g₁+b₀g₀)¢Ag₀=0,

от­ку­да

. (23)

Про­во­дя по­иск от точки x₁ вдоль на­пра­в­ле­ния -p₁, най­дем точку от­но­си­тель­но­го ми­ни­му­ма x₂=x₁-a₁p₁. Под­ста­в­ляя это x₂ в вы­ра­же­ние (14) для функ­ции F(x) и при­рав­ни­вая ну­лю про­из­вод­ную по a₁, най­дем

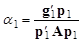(24)

ана­ло­гично то­му, как это бы­ло сде­ла­но на пер­вом ша­ге для a₀ (урав­не­ние (19)).

Для по­ис­ка ми­ни­му­ма от точки x₂ вы­бе­рем на­пра­в­ле­ние p₂, со­пря­жен­ное с дву­мя пре­ды­ду­щи­ми на­пра­в­ле­ни­я­ми пе­ре­ме­ще­ния, т. е. с g₀ и p₁, причем по­лучим его как про­ек­цию гра­ди­ен­та g₂=Ax₂+b на ги­пер­п­ло­скость N-2 из­ме­ре­ний, ор­то­го­наль­ную к ве­к­то­рам Ag₀ и Ap₁. Точки этой ги­пер­п­ло­ско­сти, по­ми­мо урав­не­ния (21), удо­в­ле­тво­ря­ют так­же урав­не­нию

(x₃-x₂)¢Ap₁=0. (25)

Но­вая (N-2)-мер­ная ги­пер­п­ло­скость це­ли­ком при­на­д­ле­жит пре­ды­ду­щей ги­пер­п­ло­ско­сти (N-1) из­ме­ре­ний. Учиты­вая, что гра­ди­ент в точке x₂ ор­то­го­на­лен на­пра­в­ле­нию по­ис­ка ми­ни­му­ма p₁, лег­ко по­ка­зать, что точка x*удо­в­ле­тво­ря­ет не толь­ко урав­не­нию (21), но и (25), и ее мо­ж­но до­с­тичь, ос­та­ва­ясь в (N-2)-мер­ном под­про­стран­с­т­ве. На­пра­в­ле­ние дви­же­ния p₂ бу­дем ис­кать в ви­де

p₂=g₂+b₁p₁, (26)

причем ко­эф­фи­ци­ент b₁ оп­ре­де­лим из ус­ло­вия при­на­д­ле­ж­но­сти p₂ рас­сма­т­ри­ва­е­мой ги­пер­п­ло­ско­сти, т. е. его ор­то­го­наль­но­сти ве­к­то­ру Ap₁ (ор­то­го­наль­ность p₂ и Ag₀ обес­печива­ет­ся ав­то­ма­тичес­ки не­за­ви­си­мо от вы­бо­ра b₁):

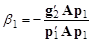. (27)

Ко­эф­фи­ци­ент a₂, оп­ре­де­ля­ю­щий сме­ще­ние точки от­но­си­тель­но­го ми­ни­му­ма x₃ от x₂ по на­пра­в­ле­нию -p₂, най­дем по фор­му­ле, ана­ло­гичной (24):

. (28)

По­сту­пая дальше аналогичным об­ра­зом, по­стро­им на­пра­в­ле­ния по­ис­ка p₃, ¼, p_N, ка­ж­дое из ко­то­рых яв­ля­ет­ся со­пря­жен­ным для всех пре­ды­ду­щих. Эти на­пра­в­ле­ния ле­жат во вло­жен­ных под­про­стран­с­т­вах умень­ша­ю­щей­ся раз­мер­но­сти, со­дер­жа­щих ис­ко­мую точку ми­ни­му­ма. Сле­до­ва­тель­но, на N‑м ша­ге за­дача све­дет­ся к по­ис­ку в од­но­мер­ном под­про­стран­с­т­ве, в ре­зуль­та­те чего бу­дет достигнута точка x*(ес­ли толь­ко ее не уда­лось найти еще рань­ше, на од­ном из пре­ды­ду­щих ша­гов).

Та­ким об­ра­зом, рас­смо­т­рен­ный ал­го­ритм га­ран­ти­ру­ет на­хо­ж­де­ние точно­го ми­ни­му­ма ква­д­ра­тич­ной функ­ции N пе­ре­мен­ных не бо­лее чем за N ша­гов. Его на­зы­ва­ют ме­то­дом со­пря­жен­ных на­пра­в­ле­ний. Час­то мо­ж­но так­же встре­тить на­зва­ние «ме­тод со­пря­жен­ных гра­ди­ен­тов», по­сколь­ку на­пра­в­ле­ния по­ис­ка яв­ля­ют­ся ли­ней­ны­ми ком­би­на­ци­я­ми ве­к­то­ров гра­ди­ен­та, вычис­лен­ных в точках по­с­ле­до­ва­тель­ных при­бли­же­ний. Од­на­ко, по­с­лед­нее на­зва­ние не впол­не точно, так как со­пря­же­ны не са­ми гра­ди­ен­ты, а их про­ек­ции на под­про­стран­с­т­ва умень­ша­ю­щей­ся раз­мер­но­сти.

Поиск по сайту: