Векторные обозначения

При рас­смо­т­ре­нии мно­го­мер­ных за­дач ес­те­ст­вен­но ис­поль­зо­вать ве­к­тор­ные обоз­начения. Со­во­куп­ность значений x₁,x₂,¼,x_n, яв­ля­ю­щих­ся ар­гу­мен­та­ми функ­ции n пе­ре­мен­ных, оп­ре­де­ля­ет по­ло­же­ние точки в n-мер­ном про­стран­с­т­ве или ее ра­ди­ус-ве­к­тор x. Та­ким об­ра­зом, функ­цию F(x₁,x₂,¼,x_n) мо­ж­но рас­сма­т­ри­вать как функ­цию ве­к­тор­но­го ар­гу­мен­та F(x).

Ес­ли в про­стран­с­т­ве за­да­ны две точки x₁ и x₂, то раз­ность v=x₁-x₂ есть не что иное, как ве­к­тор, со­еди­ня­ю­щий эти точки и на­пра­в­лен­ный от x₁ к x₂. Ес­ли x₁ – ра­ди­ус-ве­к­тор точки, а v – про­из­воль­ный ве­к­тор в n-мер­ном про­стран­с­т­ве, то их сум­ма x₂=x₁+v оп­ре­де­ля­ет точку, ле­жа­щую на пря­мой, про­ве­ден­ной через x₁ па­рал­лель­но v и на­хо­дя­щу­ю­ся от x₁ на рас­сто­я­нии, рав­ном дли­не ве­к­то­ра v.

Мно­гие ме­то­ды ис­поль­зу­ют гра­ди­ент gradF — ве­к­тор, эле­мен­та­ми ко­то­ро­го яв­ля­ют­ся час­т­ные про­из­вод­ные ¶F/¶x_i; он ука­зы­ва­ет на­пра­в­ле­ние, вдоль ко­то­ро­го функ­ция воз­рас­та­ет наи­бо­лее бы­ст­ро. Про­ти­во­по­ло­ж­но на­пра­в­лен­ный ве­к­тор -gradF (ан­ти­гра­ди­ент) ука­зы­ва­ет на­пра­в­ле­ние ско­рей­ше­го убы­ва­ния F.

Боль­шин­ст­во ме­то­дов мно­го­мер­ной оп­ти­ми­за­ции сво­дит­ся к по­с­ле­до­ва­тель­но­сти од­но­мер­ных по­ис­ков вдоль не­ко­то­рых на­пра­в­ле­ний в n-мер­ном про­стран­с­т­ве, вы­би­ра­е­мых оп­ре­де­лен­ным об­ра­зом. Про­це­ду­ру од­но­мер­ной ми­ни­ми­за­ции в мно­го­мер­ном про­стран­с­т­ве мо­ж­но опи­сать сле­ду­ю­щим об­ра­зом. Пусть x₀ – началь­ная точка, а ве­к­тор v за­да­ет на­пра­в­ле­ние по­ис­ка. Это значит, что сре­ди всех точек x, ко­то­рые ле­жат на пря­мой, про­хо­дя­щей через x₀ па­рал­лель­но ве­к­то­ру v, ну­ж­но най­ти ту, в ко­то­рой F(x) при­ни­ма­ет наи­мень­шее значение. Ра­ди­ус-ве­к­тор лю­бой точки, ле­жа­щей на ука­зан­ной пря­мой, мо­ж­но пред­ста­вить в ви­де

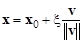, (9)

где – ев­к­ли­до­ва нор­ма (т. е. дли­на) ве­к­то­ра v, а x – сме­ще­ние (со зна­ком) точки x вдоль пря­мой от­но­си­тель­но x₀. Та­ким об­ра­зом, x яв­ля­ет­ся од­но­мер­ной ко­ор­ди­на­той, оп­ре­де­ля­ю­щей по­ло­же­ние точки на пря­мой, причем x₀ за­да­ет начало ко­ор­ди­нат (x=0), а по­ло­жи­тель­ное на­пра­в­ле­ние сов­па­да­ет с на­пра­в­ле­ни­ем ве­к­то­ра v. Ес­ли на­пра­в­ле­ние по­ис­ка за­да­но ве­к­то­ром еди­нич­ной дли­ны, т. е. , то вы­ра­же­ние (9) уп­ро­ща­ет­ся:

(9а)

По­сколь­ку x₀ и v фи­к­си­ро­ва­ны, то функ­цию на рас­сма­т­ри­ва­е­мой пря­мой мож­но считать функ­ци­ей од­ной пе­ре­мен­ной x, при­ме­няя для по­ис­ка ми­ни­му­ма лю­бой из ме­то­дов, опи­сан­ных в пер­вом раз­де­ле.

За­ме­тим, что ис­ход­ные пред­по­сыл­ки ме­то­да Дэ­ви­до­на (ну­ле­вое значение пе­ре­мен­ной в на­чаль­ной точке и по­ло­же­ние ми­ни­му­ма на по­ло­жи­тель­ной по­лу­оси) лег­ко до­с­ти­га­ют­ся пу­тем над­ле­жа­ще­го оп­ре­де­ле­ния x₀ и вы­бо­ра од­но­го из двух воз­мо­ж­ных на­пра­в­ле­ний ве­к­то­ра v для дан­ной пря­мой.

Поиск по сайту: