АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод Хука-Дживса

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Один из наи­бо­лее из­ве­ст­ных ме­то­дов пря­мо­го по­ис­ка пред­ло­жен Ху­ком и Джив­сом (R. Hooke, T. A. Jeeves) в 1961 г. Идея ме­то­да за­ключает­ся в ис­сле­до­ва­нии ло­каль­ной то­по­гра­фии по­верх­но­сти и по­пыт­ке дви­гаться даль­ше, со­хра­няя то же на­пра­в­ле­ние, ко­то­рое при­ве­ло к са­мой ни­з­кой из най­ден­ных точек. Ес­ли это на­пра­в­ле­ние при­во­дит к ус­пе­ху, оно со­хра­ня­ет­ся, в про­тив­ном случае на ос­но­ва­нии ло­каль­но­го по­ис­ка вы­би­ра­ет­ся но­вое на­пра­в­ле­ние и т. д. Ал­го­ритм вы­гля­дит сле­ду­ю­щим об­ра­зом:

а) Вы­брать началь­ную точку x0 и шаг по ка­ж­дой пе­ре­мен­ной hi. Вычис­лить F0=F(x0).

б) Ис­сле­до­вать ло­каль­ное по­ве­де­ние F(x) в ок­ре­ст­но­сти x0, а имен­но:

– в качес­т­ве те­ку­щей точки x1 при­нять началь­ную точку x0.

– для всех i от 1 до N по­в­то­рить сле­ду­ю­щие дей­ст­вия:

вычис­лить 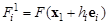, где ei – ве­к­тор еди­ничной дли­ны, сов­па­да­ю­щий по на­пра­в­ле­нию с ко­ор­ди­нат­ной осью xi. Ины­ми сло­ва­ми, от те­ку­щей точки ну­ж­но сде­лать шаг дли­ны hi по пе­ре­мен­ной xi при фи­к­си­ро­ван­ных значени­ях ос­таль­ных пе­ре­мен­ных.

ес­ли , пе­ре­не­сти те­ку­щую точку в но­вое по­ло­же­ние, т. е. , в про­тив­ном случае сде­лать шаг по xi в об­рат­ном на­пра­в­ле­нии: , и ес­ли этот шаг ока­жет­ся ус­пеш­ным, пе­ре­дви­нуть те­ку­щую точку.

Ес­ли обе по­пыт­ки пе­ре­ме­ще­ния по ко­ор­ди­на­те xi не при­ве­ли к по­ни­же­нию значения функ­ции, со­хра­нить пре­ж­нее по­ло­же­ние x1.

в) Срав­нить точку x1, до­с­тиг­ну­тую по­с­ле ис­сле­ду­ю­ще­го по­ис­ка, с ис­ход­ной точкой x0. Ес­ли x1=x0, т. е. ни в од­ном на­пра­в­ле­нии не уда­лось до­бить­ся по­ни­же­ния функ­ции, сле­ду­ет умень­шить ве­личину ша­га () и вер­нуть­ся к п. б) для по­в­то­ре­ния по­ис­ка.

г) Ес­ли по­с­ле ис­сле­ду­ю­ще­го по­ис­ка те­ку­щая точка сме­сти­лась (x1¹x0), по­про­бо­вать про­дви­нуть­ся даль­ше в том же на­пра­в­ле­нии, т. е. пе­рей­ти в точку x2=x1+(x1-x0). Это на­зы­ва­ет­ся «шаг по об­раз­цу». Значение функ­ции в точке x2 не про­ве­ря­ет­ся (оно мо­жет быть ни­же или вы­ше значения в x1).

д) Вы­пол­нить ис­сле­ду­ю­щий по­иск от точки x2 (так, как опи­са­но в п. б). В ре­зуль­та­те бу­дет най­де­на точка x3. Срав­нить значения функ­ции в точках x1 и x3.

е) Ес­ли F(x3)<F(x1), при­нять x3 за но­вую те­ку­щую точку (x0=x2, x1=x3) и сде­лать шаг по об­раз­цу, т. е. пе­рей­ти к п. г). Ес­ли же F(x3)³F(x1), то точки x2 и x3 от­вер­га­ют­ся, и про­дол­жа­ет­ся ис­сле­ду­ю­щий по­иск от точки x1 (x0=x1, пе­рей­ти к п. б).

Про­цесс за­канчива­ет­ся, ко­г­да ша­ги hi по всем пе­ре­мен­ным (по­сте­пен­но умень­ша­ю­щи­е­ся бла­го­да­ря пе­ри­о­дичес­ко­му вы­пол­не­нию п. в) ста­нут мень­ше за­дан­но­го пре­де­ла точно­с­ти.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)