Метод скорейшего спуска

Сре­ди ме­то­дов, ис­поль­зу­ю­щих пер­вые про­из­вод­ные, наи­бо­лее из­ве­с­тен ме­тод ско­рей­ше­го спу­с­ка в раз­ных мо­ди­фи­ка­ци­ях. Ос­нов­ная идея ме­то­да ос­но­ва­на на том, что ве­к­тор гра­ди­ен­та ори­ен­ти­ро­ван в на­пра­в­ле­нии наи­боль­шей кру­тиз­ны по­верх­но­сти в дан­ной точке. Дви­же­ние по ве­к­то­ру гра­ди­ен­та при­во­дит к ско­рей­ше­му ро­с­ту значений функ­ции; дви­же­ние в про­ти­во­по­ло­ж­ную сто­ро­ну (по ан­ти­гра­ди­ен­ту) ве­дет к ско­рей­ше­му убы­ва­нию функ­ции.

Про­стей­шая схе­ма ал­го­рит­ма впол­не очевид­на и вы­гля­дит сле­ду­ю­щим об­ра­зом:

Пусть x₀ – началь­ная точка. Вычис­лим в этой точке ан­ти­гра­ди­ент g₀=-gradF(x₀). Дви­га­ясь от x₀ вдоль на­пра­в­ле­ния g₀, най­дем са­мую ни­з­кую точку с по­мо­щью лю­бо­го ме­то­да од­но­мер­ной ми­ни­ми­за­ции (об од­но­мер­ном по­ис­ке вдоль за­дан­но­го на­пра­в­ле­ния см. раз­дел 2.1.2). Обоз­начим най­ден­ную точку x₁. Вычис­лим в этой точке но­вый ан­ти­гра­ди­ент g₁ и, дви­га­ясь вдоль не­го, най­дем наи­низ­шую точку x₂. По­в­то­ряя эти ша­ги, по­лучим по­с­ле­до­ва­тель­ность точек, по­сте­пен­но при­бли­жа­ю­щих­ся к ми­ни­му­му.

Рис. 7. Поиск минимума методом скорейшего спуска.

На пер­вый взгляд ка­жет­ся, что опи­сан­ный вы­ше ал­го­ритм дол­жен до­воль­но бы­ст­ро при­во­дить к це­ли, по­сколь­ку мы все вре­мя дви­жем­ся в сто­ро­ну ско­рей­ше­го убы­ва­ния функ­ции. Од­на­ко, при бо­лее вни­ма­тель­ном рас­смо­т­ре­нии ока­зы­ва­ет­ся, что его эф­фе­к­тив­ность во­все не так вы­со­ка, как мо­ж­но бы­ло ожи­дать. Пре­ж­де все­го, от­ме­тим два очевид­ных фа­к­та. Во-пер­вых, ве­к­тор гра­ди­ен­та, вы­чис­ленный в не­ко­то­рой точке x, на­пра­в­лен по нор­ма­ли к ли­нии уров­ня F(x)=const, про­ве­ден­ной через эту точку. Во-вто­рых, ес­ли на не­ко­то­рой пря­мой най­де­на точка x, в ко­то­рой функ­ция при­ни­ма­ет наи­мень­шее (для дан­ной пря­мой) значение, то эта пря­мая яв­ля­ет­ся ка­са­тель­ной к ли­нии уров­ня, про­ве­ден­ной через точку x. От­сю­да сле­ду­ет, что по­с­ле­до­ва­тель­ные на­пра­в­ле­ния по­ис­ка g₀ и g₁ вза­им­но ор­то­го­наль­ны, по­сколь­ку ве­к­тор g₀ на­пра­в­лен по ка­са­тель­ной, а g₁ – по нор­ма­ли к ли­нии уров­ня в точке x₁. Рис. 7 ил­лю­ст­ри­ру­ет эту си­ту­а­цию. Та­ким об­ра­зом, ме­тод ско­рей­ше­го спу­с­ка в из­ло­жен­ной мо­ди­фи­ка­ции ока­зы­ва­ет­ся не­мно­гим лучше, чем про­стой по­ко­ор­ди­нат­ный спуск: как там, так и здесь ша­ги де­ла­ют­ся по вза­им­но пер­пен­ди­ку­ляр­ным на­пра­в­ле­ни­ям, и един­ст­вен­ное пре­и­му­ще­ст­во гра­ди­ент­но­го ме­то­да в том, что пер­вое на­пра­в­ле­ние по­ис­ка оп­ре­де­ля­ет­ся не ори­ен­та­ци­ей ко­ор­ди­нат­ных осей, а ло­каль­ной то­по­гра­фи­ей по­верх­но­сти в ок­ре­ст­но­сти началь­ной точки. За­ме­тим, что в случае та­ких «не­удоб­ных» функ­ций, как функ­ция Ро­зен­бро­ка (рис. 6), это пре­и­му­ще­ст­во ста­но­вит­ся весь­ма со­м­ни­тель­ным.

Из­ба­вить­ся от ор­то­го­наль­но­сти по­с­ле­до­ва­тель­ных пе­ре­ме­ще­ний по­з­во­ля­ет ва­ри­ант ме­то­да ско­рей­ше­го спу­с­ка с дем­п­фи­ро­ва­ни­ем. По­с­ле спу­с­ка по ан­ти­гра­ди­ен­ту от точки x₀ до точки от­но­си­тель­но­го ми­ни­му­ма x₁, де­ла­ет­ся уко­рочен­ный шаг, т. е. те­ку­щая точка пе­ре­но­сит­ся не в x1, а в про­ме­жу­точное по­ло­же­ние , где a – ко­эф­фи­ци­ент дем­п­фи­ро­ва­ния, обычно при­ни­ма­е­мый рав­ным 0.6¸0.8. Но­вое на­пра­в­ле­ние спу­с­ка в точке x¢₁ уже не бу­дет ор­то­го­наль­ным к пре­ды­ду­ще­му, а об­ра­зу­ет с ним, как пра­ви­ло, ту­пой угол и при­бли­зит­ся к гло­баль­но­му на­пра­в­ле­нию на ми­ни­мум. Не­смо­т­ря на то, что на ка­ж­дом ша­ге спуск пре­кра­ща­ет­ся, не до­хо­дя до ми­ни­му­ма, ко­нечная цель до­с­ти­га­ет­ся за мень­шее чис­ло ша­гов.

Не­до­с­та­ток ме­то­да ско­рей­ше­го спу­с­ка с дем­п­фи­ро­ва­ни­ем — уве­личен­ный объ­ем ра­бо­ты, по­сколь­ку в ка­ж­дом на­пра­в­ле­нии про­во­дит­ся по­иск точек ми­ни­му­ма, ко­то­рые за­тем фа­к­тичес­ки не ис­поль­зу­ют­ся (они ну­ж­ны толь­ко для оцен­ки ве­личины ко­нечно­го ша­га). По­э­то­му был пред­ло­жен еще один ва­ри­ант гра­ди­ент­но­го ме­то­да, в ко­то­ром от ис­ход­ной точки по на­пра­в­ле­нию ско­рей­ше­го спу­с­ка де­ла­ет­ся шаг за­ра­нее за­дан­ной дли­ны, за­ве­до­мо мень­шей рас­сто­я­ния до точки ми­ни­му­ма. Ра­зу­ме­ет­ся, по ме­ре при­бли­же­ния к ми­ни­му­му ве­личина ша­га дол­ж­на кор­ре­к­ти­ро­вать­ся. Эф­фе­к­тив­ность это­го ме­то­да за­ви­сит от пра­виль­но­го вы­бо­ра ша­га. В пре­де­ле, ко­г­да шаг ста­но­вит­ся очень ма­лым, тра­е­к­то­рия спу­с­ка при­бли­жа­ет­ся к кри­вой, по ко­то­рой бу­дет ска­ты­вать­ся в по­ле си­лы тя­же­сти по­ме­щен­ная на по­верх­ность ма­те­ри­аль­ная точка. Эта тра­е­к­то­рия ве­дет в точку ми­ни­му­ма кратчай­шим пу­тем, так что на­зва­ние «ме­тод ско­рей­ше­го спу­с­ка» в по­л­ной ме­ре от­но­сит­ся имен­но к этой мо­ди­фи­ка­ции ал­го­рит­ма. Од­на­ко, на пра­к­ти­ке слиш­ком ма­лый шаг не­вы­го­ден, так как при­дет­ся сде­лать боль­шое чис­ло ша­гов, пре­ж­де, чем бу­дет до­с­тиг­нут ми­ни­мум. С дру­гой сто­ро­ны, чересчур боль­шой шаг при­ве­дет к из­лиш­ним от­кло­не­ни­ям от оп­ти­маль­ной тра­е­к­то­рии. По­ви­ди­мо­му, тру­д­но пред­ло­жить уни­вер­саль­ный спо­соб вы­бо­ра ша­га, при­год­ный для лю­бой за­дачи, и в этом один из глав­ных не­до­с­тат­ков рас­сма­т­ри­ва­е­мо­го ме­то­да.

2.3.2 Ме­тод Нью­то­на

Ме­тод Нью­то­на для по­ис­ка ми­ни­му­ма функ­ции не­сколь­ких пе­ре­мен­ных яв­ля­ет­ся час­т­ным случаем при­ме­не­ния ме­то­да ре­ше­ния си­с­те­мы не­ли­ней­ных урав­не­ний.

Как из­ве­ст­но, урав­не­ние ме­то­да Нью­то­на для ре­ше­ния си­с­те­мы урав­не­ний ви­да

мо­ж­но пред­ста­вить в ма­т­ричной фор­ме сле­ду­ю­щим об­ра­зом:

, (10)

где Dx – ве­к­тор по­пра­вок к началь­но­му при­бли­же­нию x₀, f – ве­к­тор, со­ста­в­лен­ный из функ­ций f_i, а J – ма­т­ри­ца Яко­би (или яко­би­ан си­с­те­мы) с эле­мен­та­ми

.

Пред­по­ла­га­ет­ся, что ве­к­тор f и ма­т­ри­ца J в пра­вой час­ти урав­не­ния (10) вычис­ле­ны в точке x₀.

Пе­ре­хо­дя к за­даче на­хо­ж­де­ния ми­ни­му­ма (ма­к­си­му­ма) функ­ции F(x), за­пи­шем ус­ло­вие экс­тре­му­ма в ви­де ра­вен­ст­ва ну­лю час­т­ных про­из­вод­ных по всем пе­ре­мен­ным:

, (11)

или ко­роче,

.

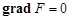Взяв началь­ное при­бли­же­ние x₀ и при­ме­няя ме­тод Нью­то­на (10) к си­с­те­ме урав­не­ний (11), по­лучим:

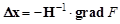, (12)

где H – ма­т­ри­ца вто­рых про­из­вод­ных (ма­т­ри­ца Гес­се или гес­си­ан) функ­ции F:

.

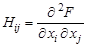Ме­тод Нью­то­на об­ла­да­ет ква­д­ра­тичной ско­ро­стью схо­ди­мо­сти к ре­ше­нию и по­то­му яв­ля­ет­ся од­ним из наи­бо­лее бы­ст­рых ме­то­дов оп­ти­ми­за­ции. Од­на­ко, он тре­бу­ет вычис­ле­ния вто­рых про­из­вод­ных, что силь­но ог­ра­ничива­ет его пра­к­тичес­кое при­ме­не­ние.

Рис. 8. Движение к минимуму в методе Ньютона.

На рис. 8 по­ка­за­на гео­ме­т­ричес­кая ин­тер­пре­та­ция урав­не­ния (12), на­гляд­но де­мон­ст­ри­ру­ю­щая раз­ни­цу ме­ж­ду ме­то­да­ми гра­ди­ент­но­го и нью­то­нов­ско­го ти­па. На­пра­в­ле­ние гра­ди­ен­та (анит­гра­ди­ен­та), от­вечаю­щее наи­бо­лее кру­то­му подъ­е­му (спу­с­ку) в точке началь­но­го при­бли­же­ния оп­ре­де­ля­ет­ся ло­каль­ной кон­фи­гу­ра­ци­ей по­верх­но­сти и, как пра­ви­ло, не сов­па­да­ет с на­пра­в­ле­ни­ем к точке экс­тре­му­ма. По­э­то­му тра­е­к­то­рия дви­же­ния к ми­ни­му­му в гра­ди­ент­ных ме­то­дах пред­ста­в­ля­ет со­бой зиг­за­го­об­раз­ную ло­ма­ную ли­нию (см. рис. 7). Ре­зуль­тат ум­но­же­ния на ма­т­ри­цу в об­щем случае мо­жет быть пред­ста­в­лен как ком­би­на­ция по­во­ро­та и из­ме­не­ния мас­шта­ба (рас­тя­же­ния или сжа­тия) ве­к­то­ра. Как вид­но из рис. 8, ум­но­же­ние ве­к­то­ра ан­ти­гра­ди­ен­та на ма­т­ри­цу H^-1 обес­печива­ет его по­во­рот в сто­ро­ну точки ми­ни­му­ма. Не­тру­д­но по­ка­зать, что в том случае, ко­г­да F(x) яв­ля­ет­ся ква­д­ра­тичной функ­ци­ей, ве­к­тор Dx, вычис­лен­ный по урав­не­нию (12), при­во­дит пря­мо в точку ми­ни­му­ма, т. е. да­ет точное ре­ше­ние за один шаг. Для функ­ции про­из­воль­но­го ви­да од­но­го ша­га уже не­до­с­та­точно, но ско­рость при­бли­же­ния к ми­ни­му­му бу­дет су­ще­ст­вен­но вы­ше, чем при спу­с­ке по ан­ти­гра­ди­ен­ту.

Поиск по сайту: