АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формулировка задачи

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

СОДЕРЖАНИЕ ДОМАШНЕГО ЗаданиЯ

В домашнем задании по дисциплине необходимо решить следующие задачи:

· оптимизация режима ЭЭС по активной мощности при учете изменения потерь активной мощности в сети;

· оптимизация краткосрочного режима ЭЭС.

Схема ЭЭС, для которой решаются задачи, приведена на рис. 1.1.

 
 
ЭС-3
ПС
 
ЭС-1
ЭС-2
 
~
~
~
 
 
 

Рис. 1.1. Схема ЭЭС

 

Каждому студенту выдается индивидуальный вариант данных о параметрах оборудования и нагрузке ЭЭС.

Решение задач выполняется с помощью учебной программы ОР10.

 

 

Оптимизация режима ЭЭС по активной мощности с учетом изменения потерь активной мощности в сети

 

Цель работы: изучение формулировки задачи, алгоритма ее решения, выполнение расчетов.

Формулировка задачи

Считаем, что в каждом из узлов схемы замещения ЭЭС имеется генерация и нагрузка 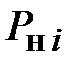. Если в действительности в каких-либо узлах схемы генерация или нагрузка отсутствует, то соответствующие члены при суммировании и при записи условий оптимальности должны быть опущены.

Задача оптимизации режима ЭЭС по активной мощности (задача оптимального распределения активной нагрузки системы между источниками) с учетом зависимости состоит в следующем: требуется найти такие допустимые мощности станций , при которых, начиная с момента времени 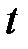за интервал времени , в течение которого нагрузки узлов ЭЭС считаются неизменными, обеспечивается минимум затрат на топливо и удовлетворяется спрос потребителей на электроэнергию. Математически это записывается так:

где 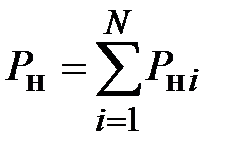– суммарная активная мощность нагрузок узлов системы.

 

Приняв в качестве балансирующей станцию узла и решая поставленную задачу методом Лагранжа, получим следующие условия оптимальности распределения активной нагрузки системы между источниками:

. (2.1)

Для рассматриваемой ЭЭС количество узлов схемы 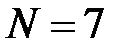. Нумерация узлов приведена на рис. 1.1. Считаем также, что =1 ч.

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)