АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формулировка задачи. Нагрузки узлов электрических систем, а, следовательно, суммарная нагрузка системы не остаются постоянными в течение суток

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

Нагрузки узлов электрических систем, а, следовательно, суммарная нагрузка системы не остаются постоянными в течение суток. В период снижения нагрузки системы снижается загрузка работающих блоков. При пониженной нагрузке блоков расход энергоресурсов на отпущенный кВт×ч возрастает. В целях экономии энергоресурсов в период снижения нагрузки системы часть работающих блоков приходится постепенно отключать. В период подъема нагрузки осуществляется пуск блоков и включение их в работу. В связи с этим, целью оптимизации краткосрочных режимов ЭЭС является не только определение оптимальной загрузки блоков, но и определение наилучшего состава работающих (включенных) блоков для каждого интервала времени периода оптимизации Т.

Обычно период оптимизации (период планирования) составляет 24 часа, начиная с момента вечернего максимума потребления текущих суток.

В работе период оптимизации разбивается на = 24 интервала времени продолжительностью =1 час. Нагрузка системы в каждом интервале времени считается известной и равной средней за интервал. Все станции ЭЭС тепловые. Если не учитывать расходы на пуски блоков, а также требования обеспечения в каждый момент времени периода Т необходимого уровня вращающегося резерва мощности, то математически задача формулируется следующим образом:

требуется найти такой состав работающих блоков и такие мощности станций в каждом интервале периода Т, чтобы в системе за период Т был израсходован минимум затрат на топливо

(3.1)

при соблюдении баланса активных мощностей в системе в каждом интервале

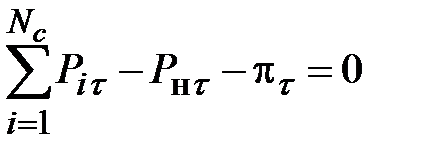, (3.2)

и ограничений по допустимой мощности станций

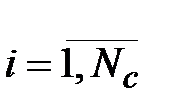; ; . (3.3)

Здесь – количество станций в системе, =3.

Решая задачу (3.1) – (3.3) методом Лагранжа, в предположении, что , можно установить, что для каждого интервала времени при заданном составе работающих блоков условия оптимального распределения активной нагрузки системы между станциями будут аналогичны (2.1).

 


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)