АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные методы интегрирования

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  3. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  4. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  5. I. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
  6. I. Основные термины и предпосылки
  7. I. ОСНОВНЫЕ ТРЕБОВАНИЯ К СИСТЕМАМ ЭЛЕКТРОСНАБЖЕНИЯ
  8. I.3. Основные этапы исторического развития римского права
  9. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  10. II. ИСЧИСЛЕНИЕ БЕСКОНЕЧНО–МАЛЫХ И ЕГО ОСНОВНЫЕ КАТЕГОРИИ
  11. II. Методы непрямого остеосинтеза.
  12. II. Основные задачи и функции

 

4.1. Непосредственное интегрирование.

Метод заключается в применении свойств 5 и 6 с использованием таблицы основных интегралов.

 


Пример 1.

 

= (по таблице основных интегралов) =

 

Пример 2.

 

Пример 3.

 

 

 

 

Пример 4.

 

 

 


Пример5.

 

 

(по формуле тригонометрии) =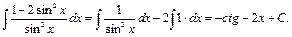

 

 

4.2. Замена переменной.

 

Метод заключается в переходе к новому аргументу интегрирования путём преобразования подынтегрального выражения по некоторой формуле.

 

 

 

При этом говорят, что в интеграле слева сделана замена переменной (подстановка) по формуле

После вычисления интеграла справа необходимо в ответе вернуться снова к аргументу x, выразив t в формуле через х.

Замечание: Часто при замене переменной удобно использовать подстановку вида , при этом .

 

Пример 6.

 

 

Пример 7.

 

 

 


Пример 8.

 

Пример 9.

 

 

Пример 10.

 

 

Пример 11.

 

 

Пример 12.

 

 

 

 

Пример 13.

 

Пример 14.

 

 

 

Пример 15.

 

 

 

Замечание. Используя простейшую замену переменной, легко получить следующие формулы:

 

 

 

 

 

 

 

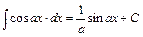
4.3. Интегрирование по частям.

 

Метод заключается в применении формулы интегрирования по частям

 

 

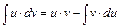
Смысл этой формулы состоит в том, чтобы в результате её применения интеграл в правой её части оказался проще первоначального. Для применения формулы интегрирования по частям подынтегральное выражение следует разбить на два множителя. Один из них обозначается через а остальная часть (содержащая ) относится ко второму множителю и обозначается через . Затем дифференцированием находится и интегрированием - функция причем в 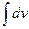произвольная постоянная берётся равной нулю.

 

Пример 16.

Пример 17.

 

 

 

Пример 18.

 

 

 


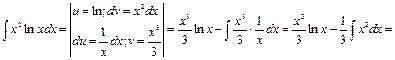
Пример 19.

 

 

 

 

Пример 20.

 

=

 

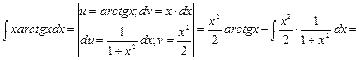
Пример 21.

 

 

 

 

 

 

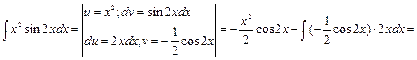
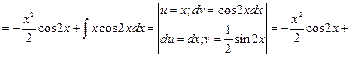
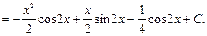
Формула интегрирования по частям применяется к интегралам следующего вида:

 

 

 

 

 

 

 

 

 

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.01 сек.)