Интегралы специального вида

1) Интегралы вида упрощаются с помощью подстановки тогда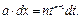

Если же в подынтегральную функцию входят радикалы с разными показателями, то следует произвести такую же подстановку, где за

нужно взять наименьшее общее кратное всех этих показателей.

Пример 22.

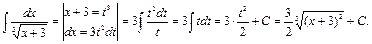
Пример 23.

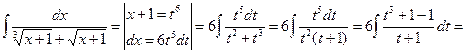
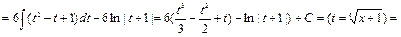
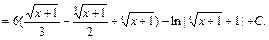
Пример 24.

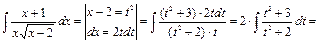
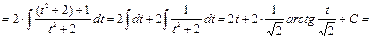
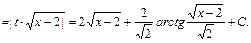
2) Интегралы вида

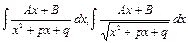
вычисляются путём выделения полного квадрата из квадратного трёхчлена

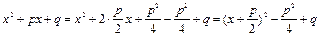
и последующей подставки

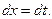
Пример 25.

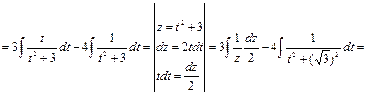
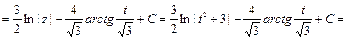
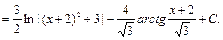
Пример 26.

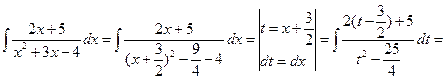
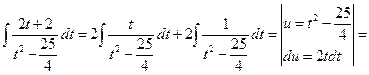
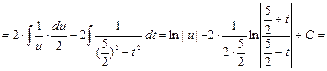
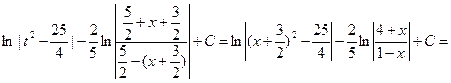
Пример 27.

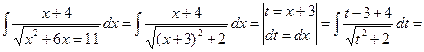
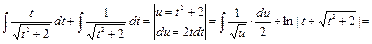
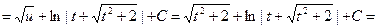
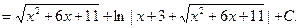
Пример 28.

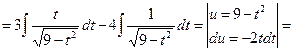
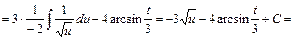
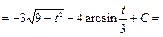
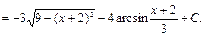
3) Интегралы вида

где целые числа,

упрощаются с помощью подстановки если нечётное число и если нечётное число.

Если чётные числа, то используют тригонометрические формулы

для понижения степеней.

Пример 29.

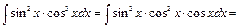
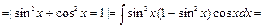
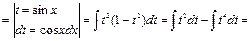
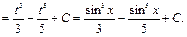
Пример 30.

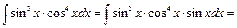
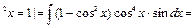
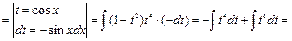
Пример 31.

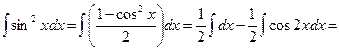
Пример 32.

Аналогично получаются более общие формулы

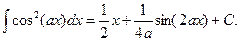
Пример33.

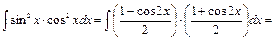
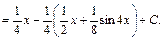
4) Интегралы вида

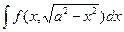
приводятся к интегралам от тригонометрических выражений подстановкой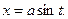

Пример 34.

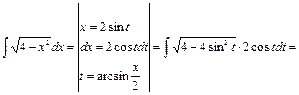
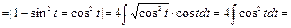
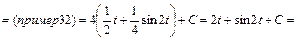
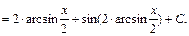
5) Интегралы вида

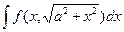
приводятся к интегралам от тригонометрических выражений подстановкой с использованием тригонометрического тождества

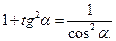
Пример 35.

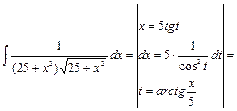
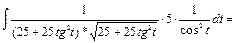
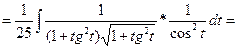
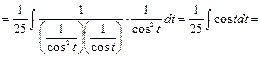
Поиск по сайту: