АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные методы вычисления определенного интеграла

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  3. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  4. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  5. I. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
  6. I. Основные термины и предпосылки
  7. I. ОСНОВНЫЕ ТРЕБОВАНИЯ К СИСТЕМАМ ЭЛЕКТРОСНАБЖЕНИЯ
  8. I.3. Основные этапы исторического развития римского права
  9. II Приближённые вычисления
  10. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  11. II. ИСЧИСЛЕНИЕ БЕСКОНЕЧНО–МАЛЫХ И ЕГО ОСНОВНЫЕ КАТЕГОРИИ
  12. II. Методы непрямого остеосинтеза.

 

9.1.Непосредственное применение формулы Ньютона-Лейбница.

 

Метод заключается в вычислении первообразной для подынтегральной функции (т.е. в вычислении неопределенного интеграла) и применении затем формулы Ньютона-Лейбница.

 

 

Пример 36.

Вычислить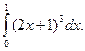

 

 

Пример 37.

Вычислить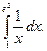

 

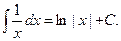
Пример 38.

Вычислить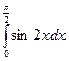

 

 

=

 

 

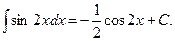
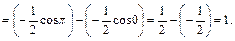
9.2. Замена переменной в определенном интеграле.

 

Метод заключается в переходе к новому аргументу интегрирования путём преобразования подынтегрального выражения по некоторой формуле, при этом пределы интегрирования изменяются и при вычислении интеграла возврат к старому аргументу не проводится.

 

 

 

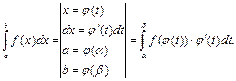
Пример 39.

 

 

 

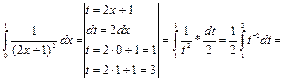
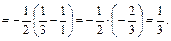
Пример 40.

 

 

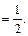
Пример 41.

 

 

=

 

 

 

 

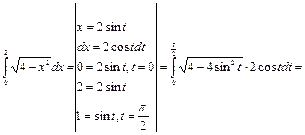
9.3. Интегрирование по частям для определенного интеграла.

 

Метод заключается в применении формулы интегрирования по частям для определенного интеграла.

 

 

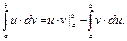
Пример 42.

 

 

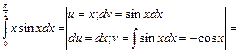
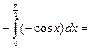
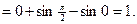
Пример 43.

 

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

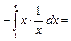
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)