АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Несобственные интегралы. При введении понятия определенного интеграла мы предполагали, что отрезок интегрирования является конечным

Читайте также:
  1. Неопределенный и определенный интегралы.
  2. Неопределенный и определенный интегралы.
  3. Несобственные интегралы
  4. Несобственные интегралы второго рода
  5. Несобственные интегралы от разрывных функций
  6. Несобственные интегралы первого рода
  7. Несобственные интегралы с бесконечными пределами
  8. Несобственные интегралы.
  9. Подраздел 9.3. Несобственные интегралы

 

При введении понятия определенного интеграла мы предполагали, что отрезок интегрирования является конечным. Если промежуток интегрирования бесконечен, то требуется специальное определение таких интегралов - они называются несобственными.

Определение. Пусть функция непрерывна на Тогда полагают:

 

Если этот предел равен числу, то несобственный интеграл 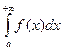называется сходящимся. Если этот предел равен бесконечности или не существует, то - расходящимся.

Пример 45.

 

т.е. интеграл сходится.

 

Пример 46.

т.е. интеграл расходится.

 

Есть и другие варианты несобственных интегралов с бесконечными пределами интегрирования - они определяются аналогично:

 

 

 

Пример 47.

 

 

Пример 48.

 

 

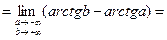(см. график в части 3,

стр. 7) =

 

Замечание. Геометрический смысл интеграла сохраняется и для несобственных интегралов - это «площадь» криволинейной трапеции, «уходящей в бесконечность», ограниченной графиком подынтегральной функции и промежутком интегрирования.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)