 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вычисление площадей фигур с помощью определенного интеграла
Из геометрического смысла определенного интеграла вытекает: если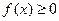 
на 
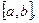то
где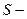 
площадь криволинейной трапеции (рис. 1).
Рассмотрим теперь случай, когда 
на 
Тогда 
на Графики этих функций симметричны относительно оси 
и поэтому площадь 
равна площади 
(рис. 8), а следовательно,
 |
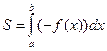или 
Тогда в общем случае, когда функция 
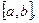меняет знак на например (рис. 9), имеем:
 |
Пусть теперь фигура ограничена графиком функции (сверху) и 
(снизу), прямыми 
и 
(рис. 10). Найдем ее площадь.
Для этого перенесем параллельно оси ординат фигуру вверх на расстояние 
так, чтобы она оказалась выше оси абсцисс (рис. 11). После этого переноса ее ограничивают графики функций 
и 
При переносе площадь не меняется и поэтому
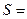площ. 
площ. 
= 
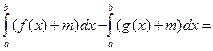
Пример 44.
Найти площадь фигуры, ограниченной параболами
 |
и 
Рис. 12
Сначала найдем точки пересечения парабол, для чего решим систему уравнений
| { | y=4x—x2 y=x2—6 |
(эти точки принадлежат и той, и другой параболе, и потому их координаты удовлетворяют одновременно уравнениям обеих парабол).
Из этой системы получаем:
откуда 
Тогда искомая площадь 
будет равна:
= 
Поиск по сайту: