Дифракция на круглом отверстии. Дифракцией света называется явление отклонения световых лучей от законов прямолинейного распространения

Глава 3 Дифракция света.

Дифракцией света называется явление отклонения световых лучей от законов прямолинейного распространения, проявляющееся при наличии препятствий на пути световых волн. Масштаб "загибания" волн зависит от отношения размеров преграды к длине волны. Возникающее в области за препятствием распределение интенсивности называется дифракционной картиной.

Строгое математическое решение этой задачи о распределении интенсивности света в дифракционной картине на основе электромагнитной теории Максвелла является сложным. Однако явление дифракции может быть довольно легко объяснено с помощью принципа Гюйгенса-Френеля, который состоит в следующем: каждая точка среды, до которой распространилась световая волна, сама становится элементарным источником вторичных волн. Все точки фронта волны являются когерентными источниками, т.е. колеблются с одинаковой частотой и в одинаковой фазе. Интенсивность света в любой точке пространства является результатом интерференции вторичных волн, приходящих от всех точек фронта волны с учетом их амплитуд и фаз.

Дифракционные явления по своему характеру разбиваются на два класса:

1. Дифракция в расходящихся (сходящихся) лучах, называемая дифракцией Френеля;

2. Дифракция в параллельных лучах, называемая дифракцией Фраунгофера.

Дифракция на круглом отверстии

Рассмотрим случай прохождения света через круглое отверстие (Рис. 21). Пусть S − CC^/ точечный источник света, −круглое отверстие в непрозрачном экране, лежащее от S на расстоянии r. Это отверстие пропускает часть сферической волны, исходящей из S. Для определения действия этой волны в точке M, лежащей на оси симметрии на расстоянии r₀ от фронта волны, мысленно разобьем волновую поверхность COC^/ на кольцевые зоны (зоны Френеля), построенные таким образом, чтобы расстояния от краев соседних зон до точки M отличались на половину длины волны, т.е.

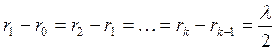
где k−порядковый номер зоны.

будут иметь оптическую разность хода λ/ 2, т.е. придут в точку M в противофазах.

Амплитуда колебаний, приходящих от отдельной зоны, зависит от площади зоны, от расстояния r_k от зоны до точки M и от угла наклона между r_k и нормалью к поверхности зоны.

Площади кольцевых зон в первом приближении (r>> λ, r₀ >> λ) не зависят от номера зоны k и приблизительно равны

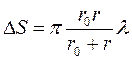
Так как с увеличением номера зоны k угол наклона между r_k и нормалью к поверхности зоны, а так же и само расстояние r_k монотонно возрастают, то амплитуда колебаний A_k, доходящих до точки M от отдельных зон, будет монотонно убывать до 0. Амплитуда суммарного колебания A в точке M зависит от числа открытых зон k. Колебания от соседних зон приходят в точку наблюдения в противофазе, следовательно, в тех точках M, для которых k−нечетно, амплитуда суммарного колебания больше, а в тех точках M, для которых k− четно, она меньше.

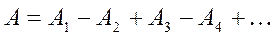
Квадрат амплитуды колебаний определяют энергию колебаний, т.е. освещенность точек экрана. Таким образом, при продвижении экрана вдоль прямой SM или при изменении диаметра отверстия CC^/, мы будем наблюдать то большие, то меньшие освещенности. В первом приближении можно считать, что амплитуда колебаний A_k линейно зависит от номера зоны:

Тогда, если в экране открыто k первых зон, амплитуда суммарного колебания в точке M равна

Так как амплитуды двух соседних зон практически одинаковы, то
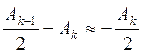тогда амплитуда суммарного колебания в точке M 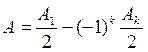(3.1)

При больших k (при большом числе открытых зон) величина A_k очень мала, следовательно, освещенность в точке M будет создаваться лишь первой зоной (даже частью этой зоны), т.е. лучи из точки S в точку M приходят практически по прямой. Таким образом дифракционная теория объясняет прямолинейное распространение света.

Наибольший практический интерес представляют случаи дифракции, наблюдающиеся при прохождении параллельных лучей (плоской волны) сквозь щель и дифракционную решетку.

Поиск по сайту: