Правило решения. 1. Формализовать задачу, т.е

1. Формализовать задачу, т.е. привести ее к виду (7.1).

2. Выписать необходимые условия:

3. Найти допустимые экстремали, т.е. решения уравнения Эйлера, являющиеся допустимыми функциями.

4. Доказать, что решением является одна из допустимых экстремалей, или показать, что решения нет.

Задачи

7.1.

7.2.

7.3.

7.4.

7.5.

7.6.

7.7.

7.8.

7.9.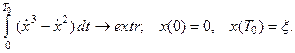

7.10.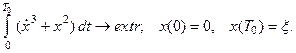

7.11.

7.12.

7.13.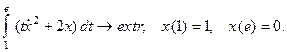

7.14.

7.15.

7.16.

7.17.

7.18.

7.19.

7.20.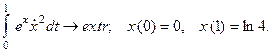

7.21.

7.22.

7.23.

7.24.

7.25.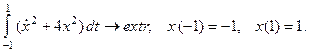

7.26.

7.27.

7.28.

7.29.

7.30.

7.31.

7.32.

7.33.

7.34.

7.35.

7.36.

7.37.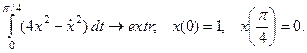

7.38.

7.39.

7.40.

7.41.

7.42.

7.43.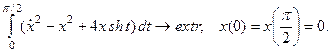

7.44.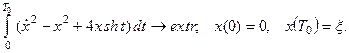

7.45.

7.46.

7.47.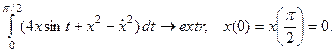

7.48.

7.49.

7.50.

7.51.

7.52.

7.53.

7.54.

7.55.

7.56.

7.57.

7.58.

7.59.

7.60.

7.61.

7.62.

7.63. 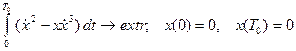(исследовать на экстремум допустимую экстремаль ).

7.64. (исследовать на экстремум

допустимую экстремаль ).

7.65.

7.66.

7.67.

7.68.

(задача о минимальной поверхности вращения).

7.69.

(задача о брахистохроне).

7.70.

Найти допустимые экстремали.

7.71.

7.72.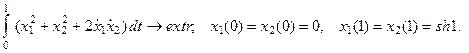

7.73.

7.74.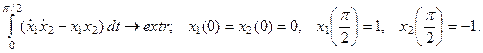

7.75.

7.76.

§8. Задачи с подвижными концами

Постановка задачи. Задачей с подвижными концами называется следующая задача в пространстве :

(8.1)

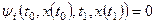, (8.2)

Здесь – заданный конечный отрезок, – функция трех, а – четырёх переменных.

В отличие от задачи Больца и простейшей задачи классического вариационного исчисления, концы отрезка интегрирования являются подвижными, и следовательно, решение задачи включает в себя некоторую функцию 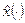и тот отрезок 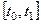, на котором она рассматривается. Значения функции в точках и 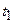в общем случае могут быть, и не заданы.

Частным случаем (8.1), (8.2) является задача, в которой один из концов или 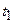– подвижный, а другой закреплен.

Тройка называется допустимой в (8.1), если и выполняются условия (8.2) на концах.

Допустимая тройка доставляет слабый локальный минимум (максимум) в задаче (8.1), если существует 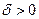такое, что для любой другой допустимой тройки , для которой и , выполняется неравенство:

При этом пишут

Поиск по сайту: