 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Поиск оптимального решения
Средство Поиск решения позволяет найти оптимальное решение в любой модели линейного программирования с помощью нескольких щелчков кнопкой мыши. На рис. 3 показано оптимальное решение для упрошенной модели Oak Product.

Рис. 3 Значения С и М, приносящие максимальную прибыль
6. Модель ЛП и ее представление в электронных таблицах
Итак, у нас есть два представления модели производства компании Oak Production: символическая (математическая) модель ЛП и ее представление в электронной таблице, которую будем называть табличной моделью.
В связи с этим может возникнуть несколько вопросов. Обязательно ли для каждой моделируемой управленческой ситуации составлять обе модели (символическую и табличную)? Почему табличная модель Oak Production выглядит именно так, а не иначе? Как использовалось средство Поиск решения для получения оптимального решения, показанного на рис. 3?
Ответим на первый вопрос: пока вы не обретете определенный опыт, следует записывать обе версии модели, как символическую (математическую), так и табличную. Электронная таблица хорошо подходит для представления моделей ЛП, особенно при проведении анализа "Что-если". Однако новичкам не следует формировать модель ЛП сразу в электронной таблице. Пока нет достаточного опыта, для создания "правильной" модели линейного программирования в Excel данный процесс лучше разбить натри этапа.
Написание и проверка символической модели ЛП. Модель записывается на бумаге в математическом виде; это не займет много времени и поможет при отладке окончательного варианта табличной модели в Excel. Затем анализируются формулировки математической задачи с целью выявления возможных логических ошибок.
1. Создание и отладка табличной модели ЛП. На основе символической модели ЛП создается ее представление в Excel. Затем производится проверка полученной табличной модели путем задания различных значений переменных решения с целью выявить возможные очевидные ошибки (например, для заведомо допустимых решений нарушаются ограничения, значения в ячейках левых частей или критерий эффективности оказываются лишенными смысла и т.д.).
2. Попытка оптимизации модели с помощью надстройки Поиск решения. Если модель некорректно сформирована, результатом чаще всего будет сообщение об ошибке. Тогда нужно исправить модель, возможно, вернувшись к первому этапу.
3. Созданная на первом этапе математическая модель полезна для целей документации, она позволяет увидеть всю модель целиком, что облегчает понимание табличной модели в Excel. Для достаточно сложных моделей проще сначала проанализировать структуру символической модели ЛП, а не ее представление в Excel. Ответим на второй вопрос ("Почему табличная модель Oak Product выглядит именно так, а не иначе?"). Модель Oak Product в Excel построена в соответствии с рекомендациями о представлении моделей в Excel, которые мы приводили ранее. Именно из-за неправильного построения моделей в Excel студентам часто не удается получить нужные результаты на этапе оптимизации. Наши рекомендации позволяют выявить скрытые ошибки в задании связей между ячейками в формулах и избежать определенных проблем интерпретации результатов, получаемых с помощью средства Поиск решения. Накопив опыт формирования моделей линейного программирования в Excel, можно пропускать этап написания символической модели. Для тех, кто такого опыта пока не имеет, предлагаем следующие рекомендации по созданию табличной модели ЛП в Excel.
· Каждая переменная решения располагается в отдельной ячейке, ячейки группируются по строкам или столбцам; каждому ограничению отводится отдельная строка или столбец таблицы. (Чаще всего переменные решения расположены в столбцах, а ограничения — в строках.)
· Переменные решения группируются в отдельный блок столбцов/строк; аналогично ограничения группируются в свой блок строк/столбцов.
· Все ячейки, содержащие переменные решения и целевую функцию, имеют заголовки в верхней части своего столбца, а все ограничения имеют заголовки в крайней слева ячейке своей строки.
· Коэффициенты целевой функции хранятся в отдельной строке, располагаясь непосредственно под или над соответствующими переменными решения; формула для вычисления целевой функции находится в соседней ячейке.
· Чтобы модель была понятней, ячейки с переменными решения и целевой функцией выделяются рамкой по границе ячеек или заливкой ячеек.
· Коэффициент перед определенной переменной решения в каком-либо ограничении записывается в ячейку на пересечении столбца (строки), содержащего данную переменную решения, и строки (столбца), содержащей это ограничение.
· В каждой строке ограничений за ячейками, содержащими коэффициенты данного ограничения, следует ячейка, в которую записано вычисленное значение функции ограничения (значение левой части неравенства), за ней следует ячейка, в которой стоит соответствующий знак неравенства, а затем ячейка, содержащая значение правой части неравенства. Дополнительно может включаться ячейка с формулой вычисления резерва, т.е. разности между значениями левой и правой частей неравенства, вычисляемой таким образом, чтобы она была неотрицательной при соответствии ограничению.
· Ячейки, содержащие правые части ограничений, должны включать константы или формулы, в которые не входят переменные решения, — все формулы в правой части, прямо или косвенно связанные с переменными решения, должны быть перенесены в левую часть с помощью алгебраических преобразований данного неравенства.
· Не следует использовать в формулах модели ЛП функции Excel ЕСЛИ, ABS, MAX, MJN и другие нелинейные функции. Такие функции могут использоваться в формулах рабочего листа, но только в том случае, если они не влияют (прямо или косвенно) на вычисление целевой функции.
· Условия неотрицательности переменных решения не обязательно включать \ в табличную модель. Как правило, они опускаются и указываются непосредственно в диалоговом окне средства Поиск решения.
Одним из результатов выполнения этих рекомендаций является то, что все основные коэффициенты модели содержатся в отдельных ячейках, поэтому их легко изменять, не меняя формул модели. Кроме того, группирование переменных решения и ограничений позволяет копировать формулы для создания аналогичных формул. Благодаря группированию также упрощается работа со средством Поиск решения, поскольку для указания переменных решения или ограничений можно использовать диапазоны ячеек рабочего листа.
7. Надстройка Поиск решения
Поиск решения — это надстройка, входящая в поставку Excel, предназначенная для оптимизации моделей при наличии ограничений, в том числе моделей линейного программирования. Для этого в надстройке используются методы и алгоритмы математического программирования, которые позволяют находить оптимальные решения для табличных моделей. Для задач линейного программирования Поиск решения использует эффективный оптимизационный алгоритм (он подходит только для моделей ЛП) под. названием симплекс-метод.
Средство Поиск решения позволяет оптимизировать линейные и нелинейные модели. (Пока мы рассматриваем более простые линейные модели.) Помните, что в оптимизируемой линейной модели все формулы, которые непосредственно содержат переменные решения и прямо или косвенно влияют на формулу, по которой вычисляется Целевая функция, должны быть линейными. Линейность модели позволяет использовать в средстве Поиск решения алгоритм симплекс-метода, который правильно работает только для формул, отображающих линейные взаимосвязи между переменными.
Все формулы Excel, используемые в табличной модели линейного программирования, должны содержать только линейные отношения между переменными, если они прямо или косвенно влияют на вычисление значения целевой функции или участвуют в функциях ограничений.
Конечно, допускаются нелинейные формулы, даже содержащие переменные решения, если эти формулы не связаны с вычислением значения целевой функции — ни прямо, ни косвенно, ни через ограничения.
Использование надстройки Поиск решения
Надстройка Поиск решения состоит из двух программных компонентов. Первая — это встроенная в Excel программа, написанная на языке Visual Basic, которая транслирует представленную на рабочем листе информацию во внутреннее представление, используемое второй программой. Вторая программа находится в памяти компьютера в виде отдельного программного модуля; именно она выполняет оптимизацию и возвращает найденное решение первой программе, которая, в свою очередь, обновляет данные на рабочем листе. Эти две программы взаимодействуют при помощи внутреннего интерфейса прикладных программ, подробности организации которого нас не интересуют. Когда выбирается команда Поиск решения в меню Excel Сервис, происходит обращение к первой программе надстройки Поиск решения, которая подготавливает таблицу к оптимизации и вызывает вторую программу-оптимизатор.
Надстройка Поиск решения, хотя и входит в поставку Excel, не подключается автоматически к этой программе. Поэтому, если в меню Сервис вы не находите команды Поиск решения, значит, надстройка не подключена. Для ее подключения выполните команду Сервис - Надстройки и в открывшемся диалоговом окне Надстройки установите флажок перед опцией Поиск решения.
Таким образом, использование надстройки Поиск решения состоит из следующих действий.
1. Откройте Excel и выполните обычные операции по созданию табличной модели. Можно создать несколько сценариев анализа "Что-если" для проверки модели.
2. После отладки модели переходите к этапу оптимизации, выбрав команду Поиск решения в меню Сервис.
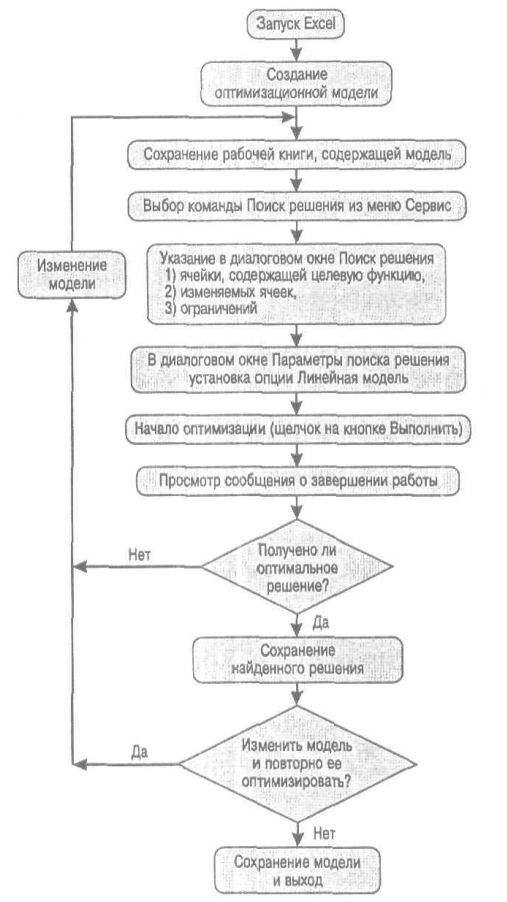
Рис. 4. Этапы работы с надстройкой Поиск решения
3. В открывшемся диалоговом окне Поиск решения укажите данные, необходимые для процесса оптимизации.
4. После задания необходимых данных (в какой ячейке содержится формула оптимизируемой целевой функции, какие ячейки включают переменные решения и т.д.) щелкните на кнопке Выполнить.
5. Поиск решения выполняет процесс оптимизации. Для небольших моделей ЛП современный персональных компьютер тратит на это всего несколько секунд, но для очень больших моделей процесс может длиться несколько минут и дольше.
6. Если в табличной модели нет ошибок, Поиск решения выведет на экран диалоговое окно Результаты поиска решения, где можно указать, обновить ли исходную модель (т.е. занести ли в ячейки значения оптимального решения) и создавать ли отчет (который впоследствии можно распечатать).
7. После этого можно продолжить выполнение анализа "Что-если", чтобы провести анализ чувствительности оптимального решения.
Последовательность работы с надстройкой Поиск решения схематично показана на рис. 4.
Терминология средства Поиск решения
После общего описания работы со средством Поиск решения вернемся к тому, какие инструкции нужно дать программе, чтобы она оптимизировала модель линейного программирования. Но сначала нужно разобраться в терминологии, которую использует это средство при оптимизации моделей ЛП. Применение специальной терминологии вызвано тем, что средство Поиск решения воспринимает только ячейки электронной таблицы, а не символическое представление моделей ЛП. С другой стороны, эти отличия чисто номинальные. Соответствие между терминами, используемыми в моделях ЛП и средстве Поиск решения, показано в табл. 4.
Таблица 4. Терминология, используемая в надстройке Поиск решения
| Термины моделей ЛП | Термины средства Поиск решения |
| Целевая функция | Целевая ячейка |
| Переменные решения | Изменяемые ячейки |
| Ограничения | Ограничения |
| Функция ограничения (левая часть неравенств ограничений) | Адреса ячеек, содержащих функции ограничения |
| Правая часть неравенств ограничений | Ограничение или граница |
Существует еще одно обстоятельство, о котором необходимо помнить при работе с моделями ЛП. Часто отрицательные решения, например, отрицательное значение количества производимых стульев в модели Oak Products и тому подобное, не имеют смысла, тогда на переменные решения налагается ограничение неотрицательности. Поскольку эти ограничения очевидны, их, как правило, не перечисляют в табличной модели ЛП. Однако при использовании средства Поиск решения условия неотрицательности переменных решения необходимо указывать — их пропуск является распространенной ошибкой. Если отрицательные решения не имеют смысла, необходимо наложить на решения модели ЛП ограничения неотрицательности, прежде чем оптимизировать модель с помощью средства Поиск решения.
8. Оптимизация модели
Научиться работать с надстройкой Поиск решения лучше всего непосредственно за компьютером. Как показано на рис. 4, первым делом нужно загрузить Excel и открыть рабочую книгу Стулья.х1s, содержащую упрошенную табличную модель Oak Product. После этого с помощью команды Сервисе Поиск решения вызывается средство Поиск решения, как показано на рис. 5.
 Рис. 5. Выбор команды Поиск решения
Рис. 5. Выбор команды Поиск решения
После того как надстройка Поиск решения загрузится в память, на экране должно появиться диалоговое окно, показанное на рис. 6. Заметьте, что по умолчанию средство Поиск решения настроено на модель максимизации, а курсор в этом диалоговом окне находится в поле Установить целевую ячейку.
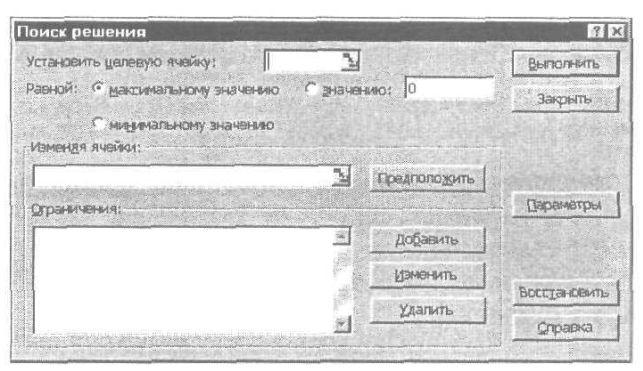 Рис. 6. Диалоговое окно Поиск решения
Рис. 6. Диалоговое окно Поиск решения
С помощью мыши можно передвигать по экрану диалоговое окно Поиск решения так, чтобы были видны различные части таблицы модели Oak Product. Это удобно, поскольку лучший способ задать ссылку на ячейку в диалоговом окне Поиск решения — щелкнуть непосредственно на данной ячейке рабочего листа. При таком способе указания ячеек не возникают опечатки.
В поле Установить целевую ячейку диалогового окна Поиск решения вводится адрес ячейки, содержащей значение целевой функции. Для модели Oak Product в это поле следует ввести D4, но лучше щелкнуть указателем мыши на этой ячейке, чтобы ввести ее адрес автоматически, как показано на рис. 8. Если адрес ячейки вводится с помощью щелчка на ячейке, Excel добавляет символы S, которые указывают на абсолютную адресацию. Можно использовать как абсолютные адреса, так и относительные (если вводить адрес ячейки вручную). В любом случае результаты будут одинаковыми.
 Рис. 8. Указание целевой ячейки
Рис. 8. Указание целевой ячейки
Совет. Если щелкнуть мышью на расположенной справа в поле ввода кнопке, диалоговое окно свернется так, что будет отображаться только текущее поле (рис. 9). Это позволяет видеть большую часть рабочего листа и удобно производить выбор ячеек. Чтобы вновь развернуть диалоговое окно, нужно нажать клавишу <Enter> или еще раз щелкнуть на кнопке, расположенной справа в поле ввода.
 Рис. 9. Сворачивание диалогового окна
Рис. 9. Сворачивание диалогового окна
Опции области Равной диалогового окна Поиск решения позволяют задать тип оптимизации. В данном случае необходимо максимизировать значение показателя эффективности, т.е. прибыль компании Oak Product. Для этого нужно щелкнуть на переключателе максимальному значению. Щелчок на кнопке минимальному значению укажет, что надо минимизировать целевую функцию (например, если показателем эффективности модели являются суммарные затраты). Можно также сделать значение целевой функции равным заданному числу, установив переключатель значению и введя это число. (Последний выбор позволяет с помощью средства Поиск решения проводить подбор параметров в моделях, содержащих много переменных и ограничений, т.е. в тех случаях, когда невозможно применить средство Подбор параметра, так как оно работает только с одной переменной при отсутствии ограничений.)
Следующее поле Изменяя ячейки позволяет указать переменные решения модели, в данном случае это диапазон В4:С4. Чтобы ввести их в данное поле, нужно щелкнуть на этом поле, а затем выделить на рабочем листе ячейки В4:С4 (рис. 10). (Можно попробовать воспользоваться кнопкой. Предположить, но при этом обычно предлагаются неверные адреса ячеек переменных решения.)
 Рис. 10. Указание изменяемых ячеек
Рис. 10. Указание изменяемых ячеек
Совет. Если вы не создали в соответствии с нашими рекомендациями такую табличную модель, в которой все ячейки переменных решения расположены вместе (что позволяет выделить сразу весь диапазон), можно указывать каждую переменную решения отдельно: щелкнуть в ячейке, ввести в поле Изменяя ячейки точку с запятой, щелкнуть в ячейке следующей переменной решения и т.д.
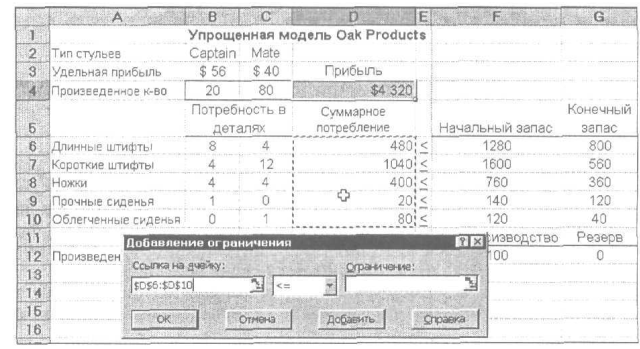 Рис. 11. Задание левой части ограничения
Рис. 11. Задание левой части ограничения
Теперь необходимо задать для средства Поиск решения ограничения. Щелчок на кнопке Добавить открывает диалоговое окно Добавление ограничения, которое позволяет вводить ограничения, как показано на рис. 11. По умолчанию предполагается, что ограничение имеет вид неравенства со знаком <=.
Если модель организована так, что неравенства одного знака расположены рядом, то их можно ввести все вместе, используя диапазоны ячеек. В противном случае придется вводить ограничения по отдельности, щелкая на кнопке Добавить диалогового окна Добавление ограничения.
Рассмотрим подробно, как задаются ограничения путем указания диапазона ячеек. Сначала в диалоговом окне Добавление ограничения курсор находится слева в поле Ссылка на ячейку. Нужно выделить ячейки рабочего листа, содержащие суммы левых частей пяти ограничений вида "<=", т.е. диапазон D6:D10, как показано на рис. 11. Заметим, что в поле Ссылка на ячейку нельзя вводить формулы — это должны быть ссылки на ячейки, которые, в свою очередь, могут содержать формулы.
Затем курсор переходит в правое поле ввода диалогового окна Добавление ограничения, и в это поле помещаются адреса пяти ячеек, содержащих соответствующие правые части ограничений, т.е. диапазон F6:F10, как показано на рис. 12. Выполнив одно действие, мы в действительности задали пять ограничений. Нужно следить, чтобы адресов ячеек левых частей было ровно столько, сколько и адресов правых частей. После этого щелкните на кнопке Добавить диалогового окна Добавление ограничения, чтобы ввести эти ограничения в спецификацию Ограничения диалогового окна Поиск решения и очистить поля диалогового окна Добавление ограничения для ввода следующих ограничений.
 Рис. 12. Задание правых частей ограничений
Рис. 12. Задание правых частей ограничений
Теперь введем ограничения вида ">=". Процедура их ввода такая же, как и для ограничений вида "<=". Курсор находится слева в поле Ссылка на ячейку, щелкаем на ячейке, содержащей левую часть ограничения, т.е. на ячейке D12. В списке поля ввода диалогового окна Добавление ограничения выбираем знак больше или равно >=, как показано на рис. 13. Обратите внимание на то, что в этом списке можно выбрать любой знак неравенства (<=, =, >=). Пока мы не рассматриваем опции цел и двоич из этого списка; они понадобятся при изучении моделей, в которых требуется, чтобы некоторые ячейки переменных решения принимали целочисленные значения.
После этого помешаем курсор в правое поле ввода диалогового окна Добавление ограничения и щелкаем на ячейке F12. Введенное ограничение должно выглядеть так, как показано на рис. 14.
 Рис. 13 Задание левой части ограничения
Рис. 13 Задание левой части ограничения
 Рис. 14. Задание правой части ограничения
Рис. 14. Задание правой части ограничения
Далее надо не забывать об условиях неотрицательности для содержимого ячеек В4 и С4. Чтобы ввести эти ограничения, сначала следует вернуться в диалоговое окно Поиск решения из диалогового окна Добавление ограничения, щелкнув на кнопке ОК в этом окне. (Если вы случайно щелкнули на кнопке Добавить, щелкните на кнопке Отмена, и вы вернетесь в диалоговое окно Поиск решения.) На данном этапе диалоговое окно Поиск решения для модели Oak. Production должно выглядеть так, как показано на рис. 15.
Чтобы определить условия неотрицательности для переменных решения, необходимо щелкнуть на кнопке Параметры диалогового окна Поиск решения. Появится диалоговое окно Параметры поиска решения (рис. 16).
Наконец, поскольку мы работаем с линейной моделью, в диалоговом окне Параметры поиска решения необходимо установить флажок опции Линейная модель, а также Неотрицательные значения и Автоматическое масштабирование. Первая из них сообщает программе, что модель является линейной, вторая налагает ограничения неотрицательности на переменные решения. Остальные опции этого окна мы пока рассматривать не будем — они в основном относятся к оптимизации целочисленных и нелинейных моделей. Щелкните на кнопке ОК, чтобы вернуться в диалоговое окно Поиск решения.
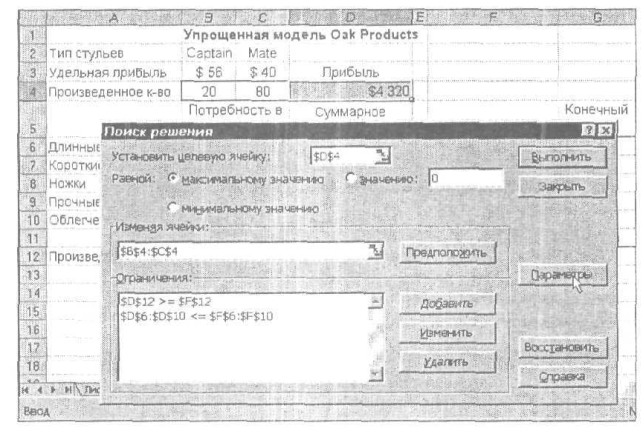 Рис. 15. Параметры поиска решения для модели Oak Product
Рис. 15. Параметры поиска решения для модели Oak Product
 Рис.. 16. Диалоговое окно Параметры поиска решения
Рис.. 16. Диалоговое окно Параметры поиска решения
Итак, полностью завершена спецификация оптимизационной модели. Мы ввели следующую информацию:
· адрес ячейки, содержащей целевую функцию, которую необходимо оптимизировать (в данном случае максимизировать);
· диапазон ячеек, которые программа должна изменять (переменные решения);
· ограничения;
· указание, что модель является моделью линейного программирования.
Теперь в диалоговом окне Поиск решения щелкните на кнопке Выполнить. За тем, как продвигается поиск решения, можно наблюдать в строке состояния в левом нижнем углу окна Excel. Однако для такой маленькой модели, как наша, оптимизация завершится очень быстро, за это время можно и не увидеть сообщения, поступающие от программы. В общем случае в процессе вычислений в строке состояния показывается число итераций и значения целевой функции при переборе множества допустимых решений задачи. Эта информация позволяет следить, как продвигается процесс оптимизации больших моделей, где он может длиться достаточно долго.
Диалоговое окно Результаты поиска решения сообщает о завершении поиска (рис. 17). То, что программа Поиск решения завершила работу, не означает, что она нашла оптимальное решение. Поэтому всегда читайте сообщение, отображаемое в верхней части данного окна! Если поспешить щелкнуть на кнопке ОК, чтобы убрать диалоговое окно Результаты поиска решения, не прочитав данное сообщение, можно пропустить важную информацию о решении. Если оптимальное решение найдено, в диалоговом окне Результаты поиска решения должно присутствовать два ключевых предложения.
· Решение найдено.
· Все ограничения и условия оптимальности выполнены.
Если хотя бы одного из этих предложений нет, программе не удалось оптимизировать модель. В таком случае либо щелкните на кнопке Справка, чтобы получить дополнительную информацию о результатах поиска и указания, что делать дальше.
 Рис. 17. Диалоговое окно Результаты поиска решения
Рис. 17. Диалоговое окно Результаты поиска решения
Если получено сообщение об успешном завершении поиска, как на рис. 17, можно или сохранить найденное решение, выбрав соответствующую опцию, или отбросить его, выбрав опцию Восстановить исходные значения, в результате ячейкам переменных решения будут возвращены значения, которые в них находились до запуска программы Поиск решения. Существует возможность также получить отчеты о решении трех типов. Каждый отчет выводится на новый лист рабочей книги.
Выберем отчет Результаты, что по умолчанию подразумевает сохранение найденного решения, и щелкнем на кнопке ОК. На рис. 18 показан отчет о результатах поиска оптимального решения для модели Oak Product. Он должен появиться на листе с названием Отчет по результатам 1 (если это имя не было использовано ранее для других листов рабочей книги). Содержимое этого листа можно свободно форматировать, распечатывать или копировать на любой лист рабочей книги. Например, в отчете, показанном на рис. 18, некоторые строки были удалены, а содержимое некоторых столбцов выровнено по центру.
 Рис. 18. Отчет о результатах для модели Oak Product
Рис. 18. Отчет о результатах для модели Oak Product
Совет. Лист с отчетом о результатах — это просто рабочий лист Excel, у которого отключено отображение сетки. Чтобы вернуть сетку, установите флажок опции Сетка в диалоговом окне Параметры (команда Сервис ^Параметры). Если вы забыли выбрать отчет и закрыли окно Результаты поиска решения, нет другого способа воссоздать отчет, кроме как повторно оптимизировать модель, чтобы окно Результаты поиска решения открылось вновь.
После выполнения всех указанных выше действий исходная таблица модели Oak Product будет выглядеть так, как показано на рис. 19. Средство Поиск решения записало в таблицу оптимальные значения переменных решения, определяющих, сколько стульев Captain и Mate нужно произвести, — 130 и 60 штук соответственно. После этого таблица пересчитывается в последний раз, чтобы вычислить максимальное значение прибыли — $9 680.
Заметим, что значения ячеек в столбце G также были изменены. Они показывают запасы различных деталей после принятия оптимального решения. Если в ячейке резерва для некоторого ограничения стоит 0, такое ограничение называется лимитирующим или связывающим. Лимитирующее ограничение не дает возможности добиться более высокой прибыли. Это значит, что увеличение прибыли путем дополнительного производства стульев Captain и/или Mate приведет к тому, что значения одной или нескольких ячеек резерва станут отрицательными, т.е. будет нарушено одно или несколько ограничений. Ограничения, имеющие ненулевой резерв (исходя из определения, резерв тогда положительный), не являются лимитирующими. Эти ограничения (по крайней мере на данном этапе) не препятствуют возможности получения более высокой прибыли. Таким образом, именно лимитирующие ограничения представляют интерес в любой модели ЛП. Нулевые значения резерва ограничений для длинных штифтов и ножек означают, что в данном случае существует два лимитирующих ограничения, два "узких места", которые препятствуют компании Oak Product производить и продавать больше стульев и таким образом получать большую прибыль.
 Рис. 19. Решение, максимизирующее прибыль
Рис. 19. Решение, максимизирующее прибыль
Если сравнить рабочий лист на рис. 19 с отчетом о результатах, показанным на рис. 18. можно заметить, что в таблице Oak Product представлена вся информация, содержащаяся в отчете о результатах. Таким образом, за исключением различий в форматировании, информация отчета о результатах полностью повторяется в исходной табличной модели. Поэтому отчет о результатах в некоторой мере избыточен, и мы будем опускать его в следующих примерах оптимизации с помощью средства Поиск решения.
После нахождения оптимального решения можно исследовать различные альтернативные варианты, выполняя анализ "Что-если" в окрестности оптимальных значений. Кроме того, можно проследить, как отразится на прибыли увеличение запаса тех или иных деталей, изменяя соответствующие ячейки правых частей ограничений и вновь запуская Поиск решения для оптимизации измененной модели. Это позволит узнать, насколько такое изменение способствует повышению прибыли. Также можно изменять коэффициенты удельной прибыли и/или коэффициенты в ограничениях, чтобы увидеть, как это отразится на прибыли. После каждого изменения необходимо вновь использовать Поиск решения для получения нового оптимального решения.
Замечание. Все настройки диалогового окна Поиск решения для каждой модели сохраняются при сохранении рабочей книги.
9. Рекомендации по поиску решения задач ЛП
Для удобства использования средства Поиск решения необходимо следовать трем следующим принципам построения моделей линейного программирования.
Во-первых, необходимо масштабировать числа в модели таким образом, чтобы разность между наибольшим и наименьшим числом в таблице не превышала шесть или семь порядков. Пусть, например, в модели одна из переменных решения — это процентная ставка (имеющая значение порядка 5%, т.е. 0,5), а показатель эффективности выражен в долларах, тогда применение средства Поиск решения может привести к неверному результату, если значение показателя эффективности будет выражаться 8-значным числом ($10 000 000. например). В этом случае разность между наименьшим (0,5) и наибольшим (10 000 000) значениями ячеек модели составит 10 порядков. Из-за этого ошибки округления, возникающие в процессе вычислений, приведут к такой потере точности, что Поиск решения не сможет правильно завершить процесс. В результате будут получены неоптимальные решения или сообщение о том, что решение не найдено.
В таких случаях нужно изменить масштаб измерения очень больших или очень маленьких чисел модели. В приведенном выше примере можно изменить денежные единицы, и выражать прибыль в миллионах долларов, а не в долларах. Это не приведет к потере общности и позволит сделать числа модели достаточно небольшими: теперь самое маленькое значение (0,5) отличается от самого большого (10) всего на 3 порядка.
Плохое масштабирование моделей является второй по значимости причиной возникновения проблем при оптимизации моделей ЛП (первая— пропуск Ограничений неотрицательности).
Совет. Начиная с версии Excel 97, помочь в разрешении проблем масштабирования может опция Автоматическое масштабирование в диалоговом окне Параметры поиска решения (см. рис. 16), однако это не гарантирует успешного устранения всех проблем.
Во-вторых, средство Поиск решения допускает, чтобы правые части неравенств были числовыми константами, адресами ячеек или формулами, что никак не влияет на процесс оптимизации. Тем не менее не следует в правую часть ограничений помещать формулы или адреса ячеек, значения которых могут меняться при оптимизации, т.е. которые прямо или косвенно связаны со значениями переменных решения.
Кроме того, не рекомендуется задавать ограничения непосредственно в диалоговом окне Поиск решения, не привязывая их к ячейкам рабочего листа и используя при этом в качестве правых частей неравенств константы, а не ссылки на ячейки модели. Рассмотрим еще один пример модели Oak Product. Предположим, что исходя из определенных соображений Джим решил, что на будущей неделе должно быть произведено не более 80 стульев Captain и не более 60 Mate. Очевидно, что оптимальное решение, полученное средством Поиск решения для исходной модели, не соответствует этим новым ограничениям, поэтому нужно исправить модель, включив в нее дополнительные ограничения, а затем оптимизировать полученную модель. Один из способов осуществления этого показан на рис, 20. Обратите внимание на два новых ограничения в верхней части списка Ограничения диалогового окна Поиск решения. Средство Поиск решения корректно оптимизирует данную модель; новое решение показано на рис. 21.
Обратите внимание на недостаток такой модификации модели Oak Production: в самой таблице новых ограничений нет, при анализе таблицы на рис. 21 оказывается, что ни одно ограничение не является лимитирующим. В результате придется при каждой оптимизации генерировать отчет о результатах и анализировать его, а также копировать информацию отчета обратно в таблицу. Кроме того, такой стиль работы со средством Поиск решения является разновидностью жесткой привязки данных. Здесь данные вводятся непосредственно в диалоговое окно Поиск решения, а не в ячейки рабочего листа. И хотя на результат вычислений это никак не влияет, структура модели становится трудно различимой, и при каждом изменении модели приходится исправлять содержимое диалогового окна Поиск решения. Мы рекомендуем добавить два новых ограничения непосредственно в табличную модель Oak Product на рабочем листе, а затем изменить диалоговое окно Поиск решения, чтобы включить новые ограничения вместе с исходными.
 Рис. 20. Новые параметры поиска решений для модели Oak Product
Рис. 20. Новые параметры поиска решений для модели Oak Product
 Рис. 21. Оптимальное решение
Рис. 21. Оптимальное решение
На основе вышесказанного можно сформулировать следующие правила хорошего стиля моделирования.
1. При задании в диалоговом окне Поиск решения правых частей ограничений всегда следует указывать ссылки на ячейки в табличной модели.
2. Ячейки правых частей неравенств в табличной модели должны содержать константы, а не формулы (точнее — не формулы, в которые явно или опосредованно входят переменные решения).
В-третьих, документированию сложных моделей содействует присвоение имен ячейкам показателя эффективности, переменных решения, функций ограничений (суммарные значениям левых частей) и ячейкам правых частей. Если это сделать, Поиск решения будет автоматически подставлять имена диапазонов для соответствующих ячеек в диалоговом окне Поиск решения.
На этом закончим изучение надстройки Поиск решения. Теперь нужно записать рабочую книгу Стулья на жесткий диск, сохраняя тем самым оптимальные решения модели ЛП и отчет о результатах.
Совет. Чтобы скопировать изображение с экрана монитора в буфер обмена, нужно нажать клиенту <PrintScreen>. Чтобы копировать в буфер обмена изображение, находящееся на переднем тане (например, диалоговое окно), нужно нажать клавиши <Ait+PrintScreen>. Из буфера обмена рисунок можно вставить в рабочий лист Excel или в другой документ в качестве иллюстрации к документации модели.
10. Пример транспортной модели
У некой компании есть два завода и три оптовых магазина-склада. Первый завод может поставлять не более 100 единиц определенной продукции, а второй — не более 200 единиц. В первом магазине-складе может храниться не более 150 единиц продукции, во втором — 200, а в третьем — 350 единиц. Цена продажи единицы продукции в первом магазине составляет $12, во втором — $14, в третьем — $15. Суммарные затраты на производство единицы продукции на заводе i и доставку ее в магазин-склад у приведены в табл. 5. Компания хочет определить, сколько единиц продукции нужно отправить с каждого завода каждому магазину, чтобы максимизировать прибыль.
Таблица 5. Удельные суммарные затраты на производство и доставку
| Магазин-склад, долл. | |||
| Завод | |||
Заметим, что здесь выбор переменных решения продиктован самой постановкой задачи. В формулировках моделей такого вида переменные решения, как правило, имеют два индекса, поэтому в таблице модели переменные решения содержатся в нескольких строках, а не в единственной строке, как это было в модели компании Oak Product. Обозначим переменные решения через Xij — количество единиц продукции, произведенных на заводе i и направленных в магазин-склад j.
 Рис. 23 Транспортная модель
Рис. 23 Транспортная модель
Для каждой переменной решения Xij. соответствующая удельная прибыль вычисляется как цена единицы продукции в данном магазине-складе минус затраты на производство и доставку этой единицы с завода i в магазин j. Например, для продукции, доставленной с завода 1 магазин-склад 1 удельная прибыль составит $12 - $8 = $4. Выполнив аналогичные вычисления для всех возможных комбинаций "завод-магазин", получим коэффициенты при слагаемых целевой функции. Таким образом, символическая модель имеет следующий вид.
Максимизировать 4X11 + 5X21 + 4X12+ 5X22 , + 3Х13 + 4X23
при ограничениях
Х 11+ Х 12 +Х13<= 100 (производственная мощность 1 завода);
X21+ X22 + X23 <= 200 (производственная мощность 2 завода);
X11 + X21<= 150 (ограничение для 1 магазина-склада);
X12+ X22<= 200 (ограничение для 2 магазина-склада);
Х13 + X23 <= 350 (ограничение для 3 магазина-склада);
Xij >=0 для всех i, j.
.
 Рис. 24. Решение транспортной задачи
Рис. 24. Решение транспортной задачи
Очевидно, что транспортная модель имеет специфическую форму. Например, все коэффициенты при переменных Xij в ограничениях равны 1. Фактически транспортные задачи входят в особый класс задач линейного программирования, которые называются сетевыми моделями.
При создании табличной модели в Excel можно разместить переменные решения Xij так, чтобы в результате получилась компактная таблица. В данном случае переменные решения будут занимать блок ячеек, а не отдельную строку, как в модели Oak Product. Табличная модель показана на рис. 23. Переменные решения, записанные в диапазоне B3:D4, задают объем продукции, произведенный определенным заводом и направленный для продажи в указанный магазин-склад. В диапазоне G3:G4 задаются ограничения производственных мощностей заводов, а в диапазоне B7:D7— ограничения объемов складов. Другие формулы имеют очевидный "бухгалтерский" смысл. На рис. 24 показано оптимальное решение данной модели, а также параметры средства Поиск решения
11. Задача составления смесей
Несмотря на то что оба рассмотренных примера — Oak Product и транспортная модель — оказались моделями максимизации, многие реальные задачи сводятся к задачам минимизации. Когда целью является прибыль, ее необходимо максимизировать, но если цель — уменьшить затраты, то приходим к задаче минимизации. В качестве модели минимизации рассмотрим следующий пример.
При создании сплава для новой продукции компании Eastern Steel используется железная руда, получаемая с четырех различных шахт. Как показал анализ, чтобы получить сплав с нужными свойствами, необходимо удовлетворить минимальные требования по трем основным элементам, которые для простоты обозначили А, В и С. В частности, каждая тонна руды должна содержать не менее 5 фунтов элемента А, 100 фунтов элемента В и 30 фунтов элемента С. Эти данные приведены в табл. 6.
Таблица 6. Требования к содержанию основных элементов
| Элемент | Минимальное содержание, фунт/т |
| А | |
| Р. | |
| С |
Руда с каждой шахты содержит все три основных элемента, но в разных количествах. Состав руды (содержание элементов) приведен в табл. 7.
Таблица 7. Состав руды с различных шахт
| Шахта (содержание | элементов, фунт/т) | |||
| Элемент | I | |||
| А | ||||
| В | ||||
| С |
Заметим, что тонна руды с первой шахты содержит 10 фунтов элемента А и, следовательно, удовлетворяет минимальному требованию к содержанию данного элемента (5 фунтов в тонне). Кроме того, она содержит 90 фунтов элемента В и 45 фунтов элемента С, таким образом требование к содержанию элемента С удовлетворяется, а к содержанию элемента В — нет. Аналогично тонна руды со второй шахты не удовлетворяет требованиям к содержанию элементов А и С, тонна руды с третьей шахты — требованиям к содержанию В и С, а с четвертой — требованию к содержанию А. Однако можно составить разнообразные смеси (в которых в различных пропорциях будут смешиваться руды с разных шахт), удовлетворяющие минимальным требованиям по всем основным элементам. Пример такой смеси: 1/2 тонны руды с шахты 1 и 1/2 тонны руды с шахты 4. Содержание элемента А в тонне такой смеси вычисляется по формуле:
содержание А = (1/2)х(содержание А в тонне руды с шахты 1) + + (1/2)х(содержание А в тонне руды с шахты 4).
Таким образом, содержание элемента А = (1/2)х 10 +(1/2)х2 = 5+1=6.
Поскольку 6>5, требование по минимальному содержанию элемента А удовлетворено.
Аналогично можно рассчитать содержание элемента В в тонне смеси:
содержание В = (1/2)х(содержание В в тонне руды с шахты 1) + < 1/2)х (содержание В в тонне руды с шахты 4).
Следовательно, содержание элемента В = (1/2)х90 + (1/2)х175 = 132,5. Наконец, содержание элемента С в тонне смеси равно (1/2)х45 + (1/2)х37 = 41.
Сравнивая полученные значения с требуемым содержанием В (100 фунтов) и С (30 фунтов), видим, что данная смесь (1/2 тонны с шахты 1 и 1/2 тонны с шахты 4) удовлетворяет всем требованиям по минимальному содержанию элементов, следовательно, она является допустимой смесью. Существует много других смесей, которые также удовлетворяют всем требованиям и являются допустимыми. Однако, поскольку руда с разных шахт имеет различную стоимость, стоимость смесей также различается. Стоимостные данные содержатся в табл. 8.
Таблица 8. Стоимость руды с различных шахт
Шахта Стоимость тонны руды, $
1 800
2 400
3 600
4 500
Например, стоимость допустимой смеси, тонна которой состоит из половины тонны руды с шахты 1 и половины тонны руды с шахты 4, вычисляется по формуле:
(1/2)х(стоимость тонны руды шахты 1) + (1/2)х(стоимость тонны руды шахты 4) =
= (1/2)х800 + (1/2)х500 = $650.
Можно попробовать сравнить эту стоимость со стоимостью других допустимых смесей. Цель компании Eastern Steel — найти самую дешевую допустимую смесь. Сформулируем данную задачу в виде модели линейного программирования.
Поскольку нужно найти оптимальный состав одной тонны смеси, зададим переменные решения следующим образом:
Т1 — часть тонны, состоящая из руды с шахты 1,
Т2 — часть тонны, состоящая из руды с шахты 2,
Т3— часть тонны, состоящая из руды с шахты 3,
Т4 — часть тонны, состоящая из руды с шахты 4.
С помощью данных табл. 7 вычислим количества основных элементов в одной тонне смеси:
количество элемента А в 1 т смеси =10 Т1 +3 Т2 +8 Т3+2 Т4(9)
количество элемента В в 1 т смеси =90 Т1 + 150 Т2 + 75Т3+175 Т4 (10)
количество элемента С в 1 т смеси = 45Т1 + 25Т2 + 20Т3 + 37Т4 (11)
Теперь скомбинируем выражения (9), (10) и (11) с требованиями по минимальному содержанию элементов, приведенными в табл. 4, и получим три ограничения.
10 Т1 +3 Т2 +8 Т3+2 Т4 >=5, (12)
90 Т1 + 150 Т2 + 75Т3+175 Т4 >= 100, (13)
45Т1 + 25Т2 + 20Т3 + 37Т4 >=30. (14)
Существуют ли в данной модели другие ограничения? Необходимо включить условия неотрицательности переменных решения Т1, Т2, Т3, Т4, однако есть еще одно важное ограничение. Поскольку тонна смеси состоит только из руды указанных четырех шахт, сумма составляющих смеси должна быть равна 1:
Т1 + Т2 + Т3+ Т4 = 1. (15)
Последнее ограничение иногда называют условием материального баланса и ограничением в виде равенства. Оно ограничивает значения переменных решения таким образом, что левая часть в точности равна правой части.
Ограничения модели линейного программирования могут быть как равенствами, так и неравенствами.
Используя данные табл. 8, легко получить формулу для вычисления стоимости тонны любой смеси:
стоимость 1 т смеси = 800 Т1 + 400 Т2 + 600Т3+ 500 Т4 .
Теперь можем составить полную символическую модель.
Минимизировать 800 Т1 + 400 Т2 + 600Т3+ 500 Т4
при ограничениях
10 Т1 +3 Т2 +8 Т3+2 Т4 >=5,
90 Т1 + 150 Т2 + 75Т3+175 Т4 >= 100,
45Т1 + 25Т2 + 20Т3 + 37Т4 >=30,
Т1 + Т2 + Т3+ Т4 = 1,
Т1, Т2, Т3, Т4 >==0.
Все функции модели являются линейными, следовательно, это модель линейного программирования.
Табличное представление модели, ее оптимальное решение, диалоговое окно Поиск решения, а также формулы представлены на рис. 25.
 Рис. 25. Модель составления рудной смеси
Рис. 25. Модель составления рудной смеси
12. Создание моделей ЛП
Чтобы попрактиковаться в формировании моделей, постарайтесь самостоятельно построить модели для следующих задач. Ознакомившись с исходными данными, старайтесь сразу же разработать символическую модель ЛП. На данном этапе не следует использовать дополнительные ограничения, логические нюансы или полет фантазии, которые могут, на ваш взгляд, сделать модель более реалистичной. Не нужно думать о том, что случится на будущей неделе, если в задаче речь о следующей неделе не идет. Предлагаемые задачи должны помочь вам научиться формулировать модели при условии, что этап перехода от реальной ситуации к абстракции уже выполнен. Чтобы вы могли проверить результаты своей работы, необходима однозначная формулировка задачи. Иными словами, в отличие от реальных ситуаций, здесь для каждой задачи существует правильный ответ. Позднее, когда у вас будет больше опыта, можно будет вносить в модели дополнительные штрихи и нюансы реальной жизни.
Пример 1. Задача об ассортименте продукции
Компания производит две марки телевизоров — Astro и Cosmo. Работают два конвейера, каждый из которых выпускает телевизоры одной марки, и два цеха, занятых производством деталей для телевизоров обеих марок. Производственная мощность конвейера, выпускающего Astro, составляет 70 телевизоров в день, а конвейера Cosmo — 50 телевизоров вдень. Цех А производит телевизионные трубки. На производство трубки для телевизора Astro требуется I ч рабочего времени, а на производство трубки для Cosmo — 2 ч. На данном этапе в цеху А производству трубок для телевизоров обеих марок может быть уделено не более 120 ч рабочего времени в день. В цеху Б изготавливаются корпуса телевизоров, причем на производство одного корпуса как для Astro, так и для Cosmo требуется I ч рабочего времени. Цех Б может посвятить изготовлению корпусов не более 90 ч рабочего времени вдень. Удельная валовая прибыль от реализации Astro и Cosmo составляет 20 и 10 долларов соответственно. Эти данные представлены в табл. 9.
Таблица 9. Данные о производстве телевизоров
| Удельные трудозатраты, ч | ||||
| Дневная производительность | Цех А | Цех Б | Удельная прибыль, | |
| Astro | ||||
| Cosmo |
Ресурс рабо- 120 90
чего времени
При условии, что компания может продать все произведенные телевизоры, каким должен быть дневной план производства (т.е. сколько телевизоров каждой марки следует производить ежедневно)?
Символическая модель ЛП для данной задачи имеет следующий вид.
А — дневной выпуск телевизоров Astro (штук/день).
С — дневной выпуск телевизоров Cosmo (штук/день).
Максимизировать 20А + 10С
при ограничениях
А<=70,
С<=50,
А + 2С<= 120,
А + С<=90,
А,С>=0.
Заметим, что, как и в модели Oak Product, в некоторые ограничения входят не все переменные решения. Например, переменная С не входит в первое ограничение (А<=70). В общем случае не обязательно, чтобы все переменные решения входили в каждое ограничение. Табличная модель Excel для данной задачи с оптимальными решениями, а также диалоговое окно Поиск решения представлены на рис. 26. Формулы для вычисления прибыли и суммарных значений в левых частях неравенств аналогичны соответствующим формулам модели составления рудной смеси, поэтому здесь и в последующих примерах мы их не приводим. Для ограничения по трудозатратам в цеху Б и для ограничения производственной мощности по выпуску телевизоров Astro резерв оказался не в точности равен нулю. Такая ситуация достаточно типична: во многих решениях, предлагаемых средством Поиск решения, резерв может принимать очень маленькие положительные или отрицательные значения, поскольку программа имеет ограниченную точность вычислений. Эти малые значения отражают предел вычислительной точности Excel и на практике могут считаться равными 0.
 Рис. 26. Модель задачи об ассортименте продукции
Рис. 26. Модель задачи об ассортименте продукции
Пример 2. Задача составления смеси
Жестяная банка корма для собак весом 16 унций должна содержать как минимум следующие количества питательных веществ: белков — 3 унции, углеводов — 5 унций и жиров— 4 унции. Нужно смешать четыре вида каш в различных пропорциях, чтобы получить наиболее дешевую банку собачьего корма, удовлетворяющую требованиям по содержанию питательных веществ. Содержание питательных веществ и цена каждой каши в расчете на 16 унций приводятся в табл. 10.
Таблица 10. Данные о цене и содержании питательных веществ
| Содержание питательных веществ и цена | ||||
| Каша | Содержание белков, | Содержание углеводов, | Содержание жиров, | Цена, долл. |
| унции | унции | унции | ||
Модель линейного программирования для задачи по составлению корма для собак имеет следующий вид.
Минимизировать
4х1 + 6х2 + Зх3 + 2х4
при ограничениях
Зх1+ 5 х2+ 2х3 + З х4 >= 3,
7х1+ 4 х2 + 2х3+ 8 х4 >= 5,
5х1+ 6 х2 + 6x3 + 2x4>=4,
х1 + х2 + х3 + х4 = 1,
х1, х2, х3, х4 >= 0.
Табличное представление модели, оптимальное решение, а также параметры для средства Поиск решения показаны на рис. 27.
 Рис. 27. Модель задачи по составлению оптимального корма для собак
Рис. 27. Модель задачи по составлению оптимального корма для собак
Заметим, что в предыдущем примере дробные значения переменных решения могут считаться недопустимыми (если не предполагать, что они представляют средний ежедневный выпуск). А в этом примере дробные значения естественны и допустимы.
Пример 3. Составление расписания
Управляющий персоналом университета должен составить расписание охраны территории университета, удовлетворяющее требованиям, представленным в табл. 11.
Таблица 11. Требования к организации охраны территории
Время Минимальное число офицеров охраны
0.00-4.00 5
4.00-8.00 7
8.00-12.00 15
12.00-16.00 7
16.00-20.00 12
20.00-24.00 9
Офицеры дежурят посменно, продолжительность смены 8 ч. На каждый день установлено 6 смен. Время начала и конца каждой смены показано в табл. 12.
Таблица 12. Расписание смен
Смена Время начала Время окончания
1 0.00 8.00
2 4.00 12.00
3 8.00 16.00
4 12.00 20.00
5 16.00 24.00
6 20.00 4.00
Управляющий персоналом хочет определить, сколько офицеров назначить в каждую смену, чтобы минимизировать их количество и при этом удовлетворить требования к организации охраны. Переменные решения можно определить следующим образом.
Х1 — число офицеров, дежурящих в смену I;
X2 — число офицеров, дежурящих в смену 2;
Х6 — число офицеров, дежурящих в смену 6.
Целевая функция имеет вид Х1+ Х2 + Х3 + Х4 + X5 + Х6. При формулировке ограничений нужно убедиться, что определенный набор значений переменных Х1..., Хь удовлетворяет требованиям по организации охраны территории. Нужно выбрать некий механизм, который позволит определить, какие офицеры находятся на дежурстве в течение каждого из указанных в требованиях интервалов времени. В этом может помочь табл. 13. Так, офицеры, дежурящие в первую смену, находятся на посту в течение первых двух временных интервалов и т.д. С помощью таблицы также можно определить (суммируя значения в одном столбце), сколько офицеров находится на дежурстве в течение каждого временного интервала (например, в первый интервал дежурит x1 + x6 офицеров; поэтому первое ограничение выглядит следующим образом: x1 + x6 >= 5).
Таблица 1 Количество офицеров, дежурящих в течение каждого временного интервала
Временной интервал
Смена 0.00-4.00 4.00-8.00 8.00-12.00 12.00-16.00 16.00-20.00 20.00-24.0 0
1 x1 x1
2 x2 x2
3 x3 x3
4 x4 x4
5 x5 x5
6x6 _____________________________________________ x6
Надо 5 7 15 7 12 9
Символическая модель имеет следующий вид.
Минимизировать Х1+ Х2 + Х3 + Х4 + X5 + Х6.
при ограничениях
Х1+ Х6 >=5,
Х1+ Х2 >=7,
Х2+ Х3 >=15,
Х3+ Х4 >=7,
Х4+ Х5 >=12,
Х5+ Х6>=9,
Хi >=0, i= 1,2,..., 6.
Данная задача является еще одним примером, в котором переменные решения должны принимать целочисленные значения. Табличная модель с оптимальными решениями, а также параметры для средства Поиск решения представлены на рис. 28.
Задачи такого типа использовались при составлении расписания дежурств операторов телефонных станций. Как правило, каждый час разбивается на 15-минутные интервалы; в сутках 24 часа, следовательно, имеется 94 ограничения. Количество переменных решения определяется тем, сколько существует возможных смен.
 Рис. 28. Модель задачи по составлению расписания дежурств
Рис. 28. Модель задачи по составлению расписания дежурств
Пример 4. Анализ безубыточности при наличии ограничений
Компания Longer Boats производит три вида высококлассных гоночных яхт — Sting, Ray и Breaker. Соответствующие данные о затратах и доходах на ближайший плановый период представлены в табл. 14.
Таблица 14. Данные о затратах и доходах компании Longer Boats
| Яхты | Цена, долл. за единицу | Переменные затраты, за единицу | Фиксиров. затраты |
| Sting | 10 000 | 5 000 | 5 000 000 |
| Ray | 7 500 | 3 600 | 3 000 000 |
| Breaker | 15 000 | 8 000 | 10 000 000 |
Как свидетельствуют эти данные, фиксированные затраты в каждом случае весьма значительные. Фиксированные затраты — это всевозможные расходы, которые существуют независимо от того, какое количество продукта производится. Так, для яхт класса Ray потребуется затратить те же самые S3 000 000 независимо от того, будет построена 1 яхта этого класса, 40 яхт или 0. Высокие фиксированные затраты включают в себя затраты на модификацию проекта, создание макета и испытание яхты в бассейне.
На рис. 25 представлено определение точки безубыточности (критического объема производства) для яхт класса Sting. Как следует из графика, если компания Longer Boats будет производить только яхты Sting, то для того, чтобы добиться безубыточности, ей потребуется выпустить не менее 1 000 яхт.
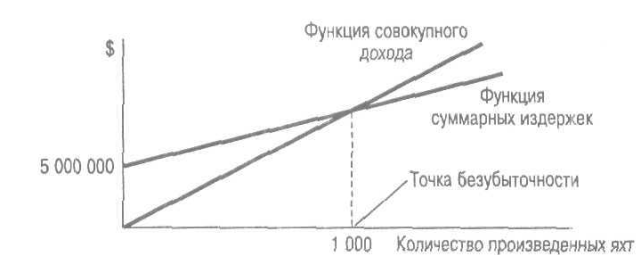 Рис. 25. Анализ безубыточности для производства яхт Sting
Рис. 25. Анализ безубыточности для производства яхт Sting
Однако перед компанией Longer Boats стоит более сложная задача. Во-первых, на следующий плановый период руководство компании уже заключило контракт на производство 700 яхт Sting. Во-вторых, еще один клиент заказал 400 яхт Breaker, и руководство заинтересовано в выполнении данного заказа. В-третьих, анализ рынка, проведенный отделом маркетинга компании, свидетельствует, что следует произвести не более 300 яхт Ray. Руководство компании хочет выяснить, сколько каких яхт необходимо продать, чтобы добиться безубыточности. Таким образом, необходимо учесть наличие трех моделей, а также заключенных соглашений.
Начнем с общих положений: точка безубыточности характеризуется тем, что суммарный доход равняется суммарным затратам. Поскольку компания Longer Boats создана относительно недавно и испытывает определенные сложности с платежами (что связано с быстрым ростом компании), руководство заинтересовано в том, чтобы минимизировать расходы. Поскольку фиксированные затраты придется нести в любом случае, целью можно считать минимизацию суммарных переменных затрат. Таким образом, поставлена задача найти производственный план с наименьшими переменными затратами, соответствующий ограничениям и приносящий доход, равный суммарным затратам.
Чтобы получить уравнение точки безубыточности в зависимости от количества произведенных яхт определим переменные решения следующим образом.
S — количество произведенных яхт класса Sting,
R — количество произведенных яхт Ray,
В — количество произведенных яхт Breaker.
Тогда уравнение точки безубыточности примет вид
10000S + 7500R + 15000B = 5000S + 3600B + 8000B - 18000000
или
5000S+ 3900R + 7000B= 18000000.
Заметим, что существует бесконечное число множеств значений S, R и 5, удовлетворяющих данному ограничению: в многопродуктовой модели существует множество точек безубыточности, в то время как для однопродуктовой модели точка безубыточности одна. Поэтому при выпуске нескольких продуктов руководство должно указать дополнительные ограничения, которые позволят найти конкретную точку безубыточности, представляющую интерес. Постоянные затраты придется нести в полном объеме независимо от количества произведенных яхт, поэтому, чтобы добиться минимизации инвестиций, необходимо минимизировать суммарные переменные затраты. Таким образом, целевая функция (суммарные переменные затраты) имеет вид
5000S+3600R+8000B.
Полная модель с учетом ограничения безубыточности, предварительно установленных требований и ограничений спроса выглядит следующим образом:
минимизировать 5000S + 3600R + 8000B
при ограничениях
5000S + 3900R + 7000B = 18 000 000,
S>=700,
В>=400,
R<=300,
S>=0, R>=0, B>=0.
Табличная модель, оптимальное решение и параметры для средства Поиск решения представлены на рис. 29.
 Рис. 29. Модель нахождения точки безубыточности
Рис. 29. Модель нахождения точки безубыточности
17. Разработка моделей ЛП
Изучая рассмотренные примеры моделей линейного программирования, вы могли убедиться, что их создание сводится к разумной и тщательной спецификации составляющих модели (переменных решения, ограничений, целевой функции и т.д.) в соответствии с символической линейной оптимизационной моделью. Однако в формировании моделей ЛП есть свои ловушки, которых следует избегать. Рассмотрим некоторые ошибки, часто встречающиеся при создании моделей.
· Как всегда при моделировании, не следует сразу излишне детализировать модель, поскольку тогда трудно сформулировать целостную и согласованную модель. При создании табличной версии модели в Excel эти несогласованности превратятся в трудно обнаружимые логические дефекты таблицы. Поэтому лучше начать с формирования минимально достаточного множества переменных решения и ограничений. Впоследствии можно усложнить изначально простую модель, добавив дополнительные переменные и ограничения.
· Не следует (по крайней мере на начальных этапах) включать в модель нелинейные зависимости. Старайтесь использовать линейные уравнения, для чего можно в узком диапазоне значений переменных (заданном с помощью дополнительных ограничений) аппроксимировать более сложные нелинейные связи линейными зависимостями. Отметим, что оптимизировать нелинейную модель гораздо труднее). Кроме того, нелинейная оптимизация имеет свои сложности и ловушки. Если же в модель необходимо включить некие нелинейные связи, лучше сначала разработать упрощенную линейную модель, а нелинейные связи добавить позже.
Поиск по сайту: