Вычисление резерва

За исключением ячеек G11 и GI2, все элементы таблицы имеют очевидный смысл. Ос­талось объяснить, что представляет собой элемент под названием Резерв в ячейке G12. В моделях ЛП термином резерв обозначается неотрицательная разность функции огра­ничения и его правой части.

Часто предпочтительней использовать более содержательные названия, чем резерв, например, Конечный запас (т.е. запас на конец недели, как в ячейке G5). Бо­лее того, вычисления в столбце G однотипны. Их назначение — показать, насколько близко значение функции ограничения к значению правой части неравенства, при этом нулевой резерв свидетельствует о том, что в ограничении достигнуто равенство. Напри­мер, формула =F6-D6 в ячейке G6 соответствует ограничению для длинных штифтов 8С + 4М <= 1280. Здесь из правой части данного ограничения вычитается левая часть. Та­ким образом, значение запаса на конец периода (или резерв для данного ограничения) — это количество неиспользованных длинных штифтов. Однако в ячейке G12, соответствующей ограничению С + М >= 100, записана формула "левая часть ограни­чения минус правая часть"; такой порядок вычитания обусловлен тем, что резерв должен быть неотрицательной величиной для допустимых решений. Итак, сформулируем сле­дующее правило.

Для ограничений типа <= при вычислении резерва из правой части неравенства вычита­ется левая часть. Для ограничений типа >= при вычислении резерва из левой части неравенства вычитается правая часть.

Хотя вычисление резерва и не является обязательным, оно очень полезно. Например, сразу становится очевидным, что производственный план на рис. 1 недопустим, по­скольку запас на конец периода в ячейке G8 получился отрицательным.

Один из очевидных способов использования полученной модели компании Oak Product — проведение анализа "Что-если" для различных решений (т.е. различных значений производ­ства стульев Captain и Mate). Для этого следует ввести соответствующие значения в ячейки В4 и С4 и просмотреть значения в ячейке D4, представляющие недельную валовую прибыль. При этом нужно следить, чтобы значения резерва в ячейках G6:G12 были неотрицательными. Если ввести в ячейку В4 значение 20, а в ячейку С4 значение 80 (что означает С= 20, М= 80), то результи­рующая таблица будет выглядеть так, как показано на рис. 2.

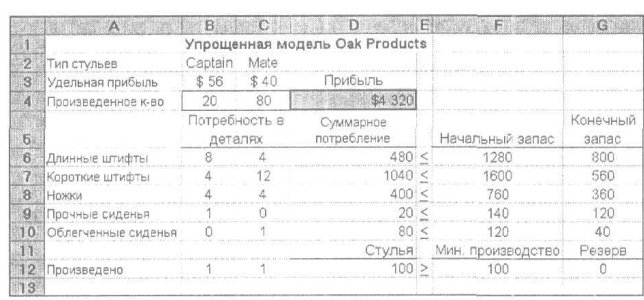Рис. 2. Модель производства компании Oak Products для С=20и М=80

Совет. Как вы увидите, знаки неравенств в столбце Е, разделяющие значения левых и правых частей ограничений, не используются при работе со средством Поиск решения и поэтому не являются обязательными. Однако их использование помогает при формализации модели.

Используя рабочую книгу Стулья.xls, попробуйте, подставляя различные значения переменных С и М, получить максимальную прибыль, как это делали Том и Джим. Вы скоро поймете, что найти наибольшую прибыль, не нарушая ограничений, непростая за­дача даже для такой упрощенной модели.

Поиск по сайту: