Учебный год

Вопросы к экзамену по курсу Микроэкономика-2

1. Аксиоматика ординалистской версии теории потребительского выбора. Предпочтения потребителя и ординалистская функция полезности. Предельная норма замещения.

Объект потребительского выбора – товарный набор, обладающий свойствами:

· Совершенной делимости (в набор может входить, например, четверть автомобиля)

· Неотрицательности (кол-во товаров в наборе больше или равно 0)

· Аддитивности (можно складывать между собой количества благ, входящих в разные наборы, получая новые наборы)

Главная идея ординалистской теории состоит в том, что потребители могу сравнивать и ранжировать товарные наборы, но не могут измерять их полезность.

Предпосылки анализа поведения потребителя:

· Принцип рациональности поведения потребителя (выбор лучшего из доступного)

· Свобола и суверенитет выбора

· Полнота информации, необзодимой для принятия решения

Аксиоматика ординалистской теории потребительского выбора:

· Аксиома совершенной упорядоченности и сравнимости (потребитель может оценить и расставить все наборы с точки зрения удовлетворения потребности)

· Аксиома транзитивности (если A>B>C или A=B>C, то A>C, где A,B,C – наборы товаров)

· Аксиома рефлексивности (A>=A, каждый набор принадлежит по меньшей мере одному множеству безразличия – тому, которое содержит как минимум сам набор А)

· Аксиома ненасыщения (потребитель предпочитает большее кол-во товара меньшему)

· Аксиома непрерывности (можно изменить кол-во товара в наборе и компенсировать изменение изменением кол-ва другого блага)

· Аксиома предпочтения среднего набора

Ординалистская функция полезности – это такой способ предписывания каждому возможному потребительскому набору некого порядкового номера, при котором каждый более предпочтительный набор получает больший индекс, чем менее предпочтительный.

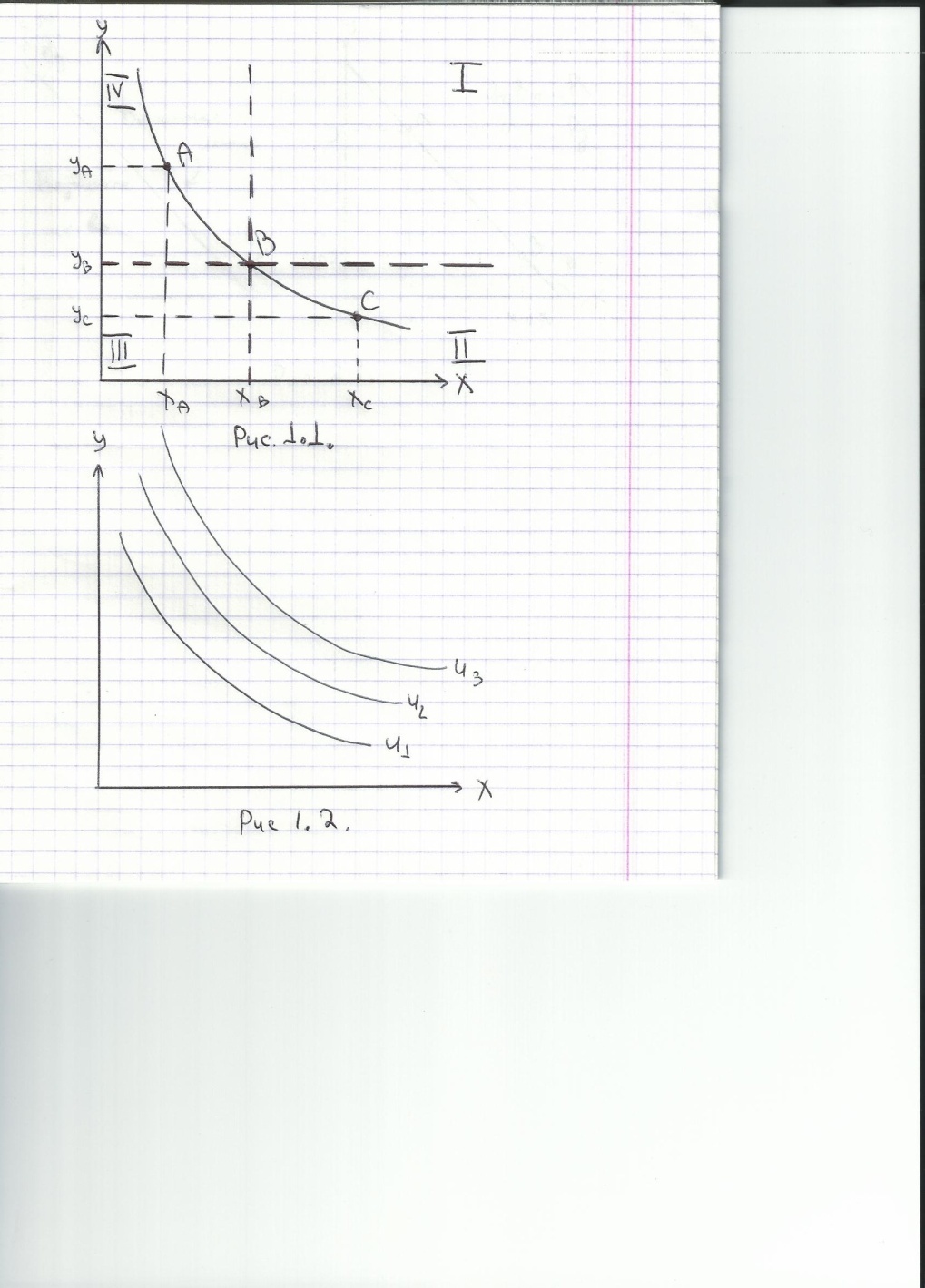
Кривая безразличия – это множество точек, каждой из которых соответствует такой набор из 2-х благ, что потребителю безразлично, какой из наборов выбрать. (рис.1.1.)

Карта безразличия – это набор кривых безразличия, который служит графическим изображением ординалистской функции полезности. Чем выше кривая, тем предпочтительнее ее наборы. (рис.1.2.)

Свойства кривых безразличия:

· Может быть проведена через любую точку пространства товаров

· Имеет отрицательный наклон

· Набор, принадлежащий более высокой кривой предпочтительнее

· Кривые не пересекаются и выпуклы к началу координат

Предельная норма замещения (MRSxy) – это кол-во товара У, на которое должно быть сокращено его потрбеление ради увеличения блага Х на 1 с тем, чтобы уровень удовлетворения не изменился.

MRS=-∆У/∆X=MUx/MUy

MRS убывает по мере движения вдоль кривой безразличия.

2. Бюджетное ограничение. Влияние на бюджетное ограничение изменений дохода и цен. Выбор потребителя в ординалистской теории полезности.

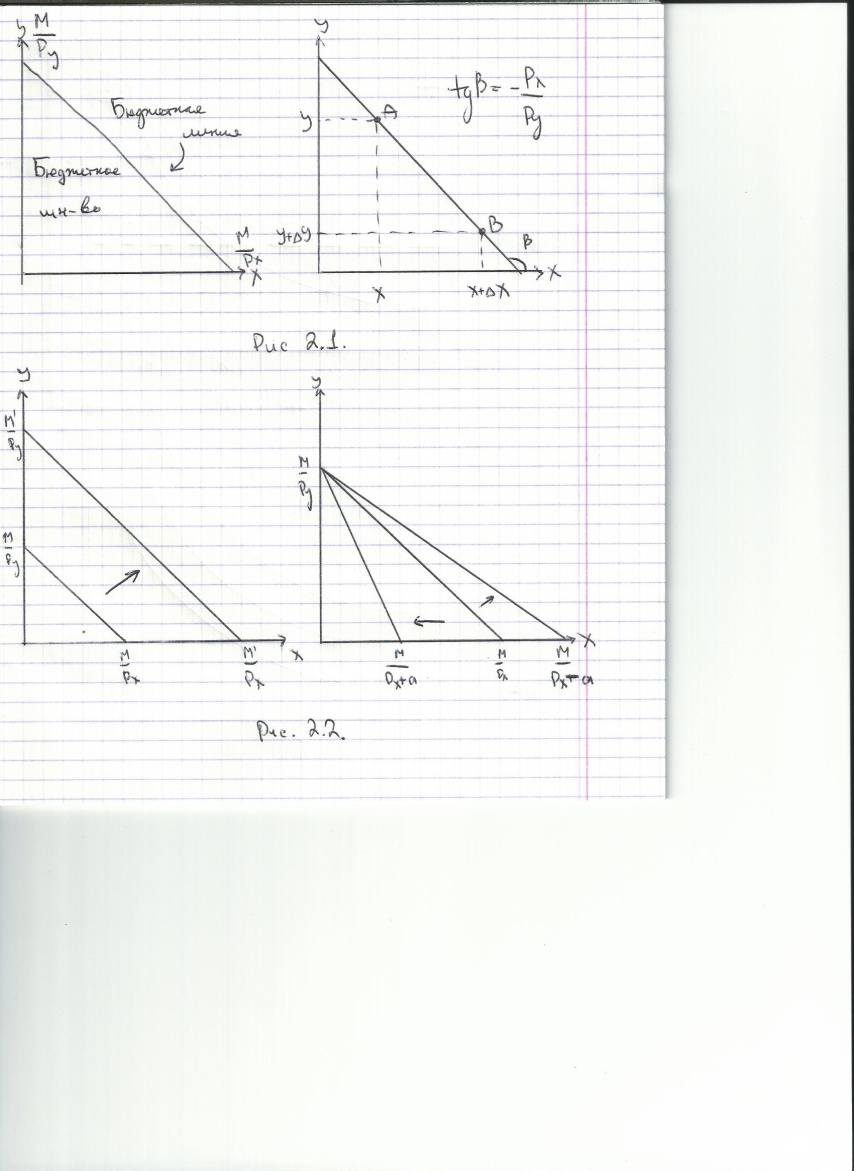Множество доступных потребителю наборов товаров Х и Упри доходе М и цена Рх, Ру – бюджетное множество потребителя.

РхХ+РуУ=<M

Бюджетная линия – множество точек, в которых потребитель тратит весь свой доход, т.е. РхХ+РуУ=M

При росте дохода потребителя, его бюджетная линия сдвигается параллельно исходной вправо вверх, при снижении – влево вниз.

Это видно из уравнения: У=(-Рх/Ру)Х+М/Ру.

Изменение величины дохода не затрагивает наклона бюджетной линии, влияя лишь на пересечение с вертикальной осью.

При изменении цены товара имеет место поворот бюджетной линии вокруг точки пересечения ее с вертикальной осью. Поворот осуществляет во внешнюю сторону при уменьшении цены и вовнутрь при удорожании товара.

Описание предпочтений потребителя с помощью непрерывной вещественной функции полезности позволяет свести производимый им выбор лучшего набора из доступного к решению задачи максимизации полезности при заданном бюджетном ограничении.

Max U(X,Y) при PxX+PyY=M

Классический случай существования единственного внутреннего оптимума потребителя имеет место при типичной форме кривых безразличия, когда наивысший уровень полезности достигается в точке касания линии бюджетного ограничения и кривой безразличия.

MRSxy = Px/Py

Индивид платит за единицу товара Х столько, сколько хочет уплатить, и дальнейший обмен не имеет смысла.

Краевой оптимум – это выбор, при котором потребление одного из товаров равно нулю, т.к. равенство MRSxy = Px/Pу недостижимо.

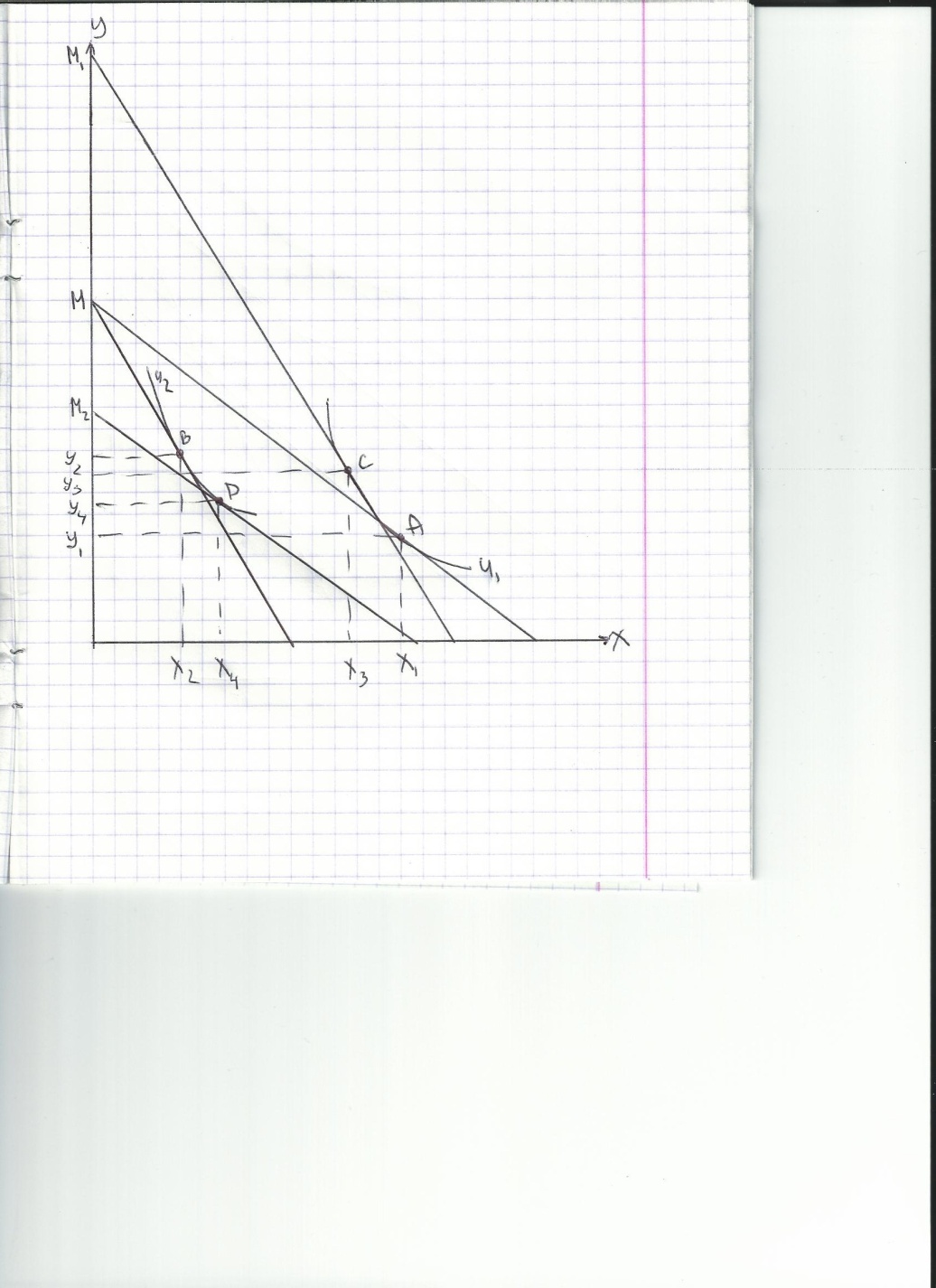
3. Влияние изменения цен на выбор потребителя. Кривая «цена – потребление», кривая маршаллианского спроса.

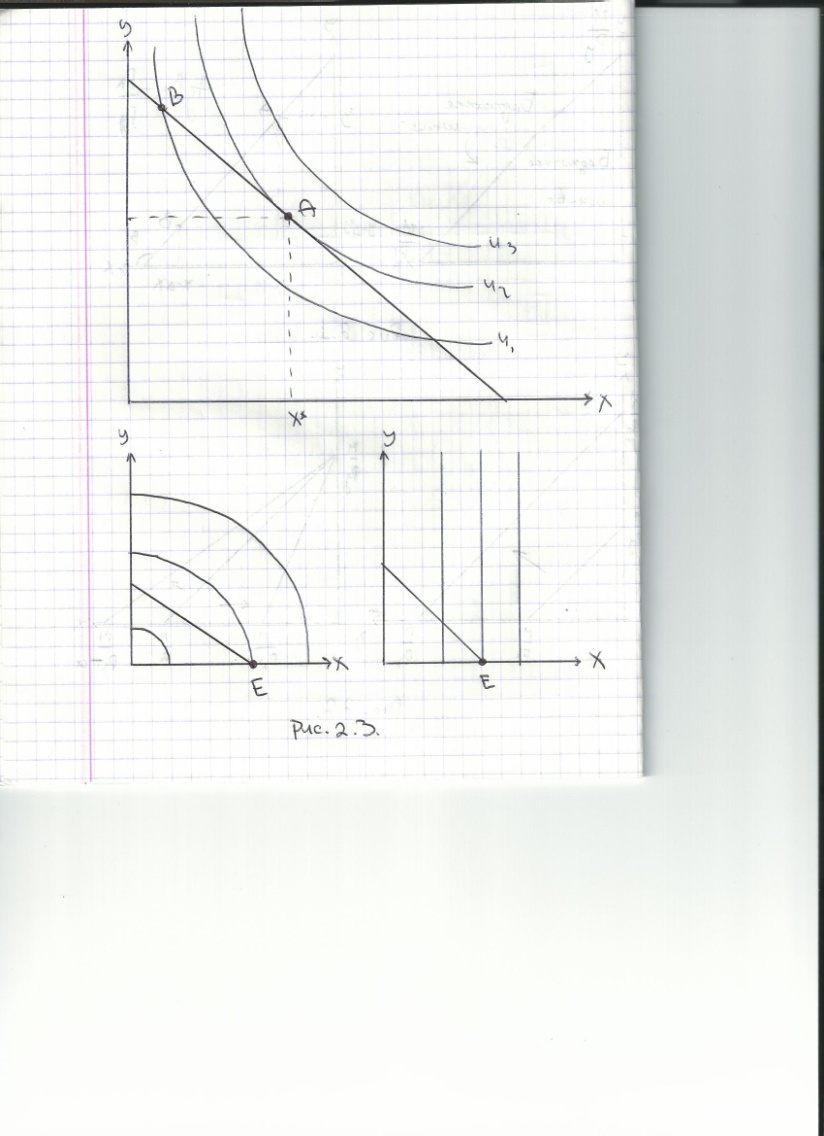
Проследим изменение оптимума потребителя, обусловленное изменением цены товара Х. На этой основе построим кривую «цена-потребление», а затем и кривую спроса.

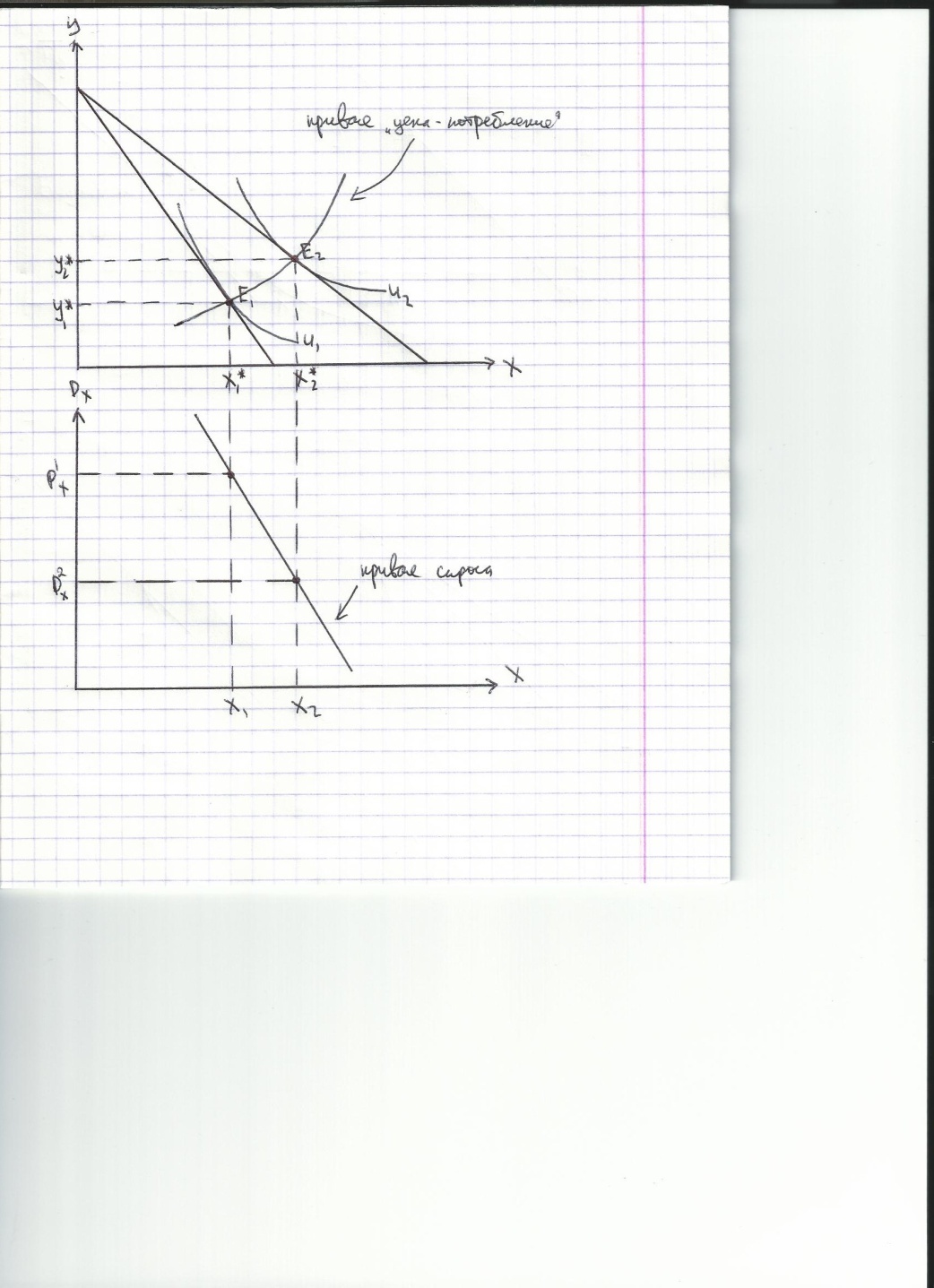Пусть цена товара Х снижается, что вызывает поворот линии бюджетного ограничения и смещение оптимума потребителя из Е1 в Е2. Линия, соединяющая все полученные таким образом оптимальные комбинации называется кривой «цена-потребление». Можно построить кривую спроса. Эта кривая выражает отрицательную зависимость между ценой товара и количеством спроса на него. Кривая «цена-потребление» дает информацию об изменении кол-ва спроса на оба товара, а кривая спроса – на отдельный товар.

Если с падением цены товара Х кол-во спроса на У растет, то товар У выступает по отношению к Х общим комплементом, и кривая «цена-потребление» имеет положительный наклон. Однако при сохранении отрицательности наклона кривой спроса на Х, У может выступать по отношению к Х и общим субститутом (кривая ц-п имеет положительный наклон) или независимым товаром (кривая ц-п горизонтальна).

4. Влияние изменения дохода на выбор потребителя. Кривая «доход – потребление», кривая Э. Энгеля. Обобщенный закон Э. Энгеля.

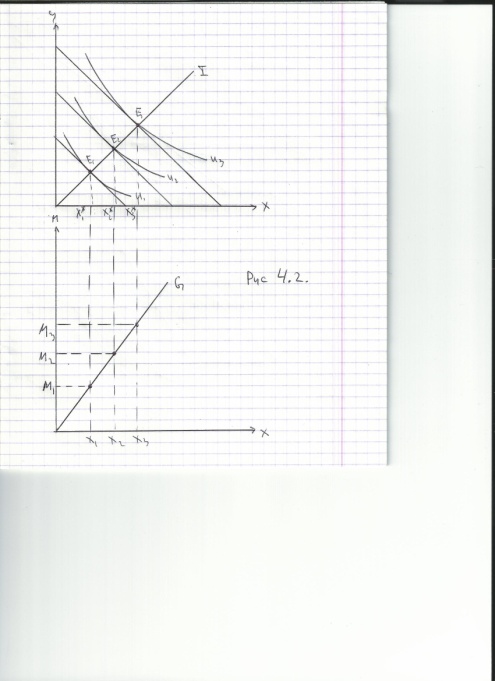
Проследим изменения оптимума потребителя, обусловленные изменением имеющегося в его распоряжении дохода. На этой основе построим пары кривых «доход-потребление» и Энгеля.

MPC – предельная склонность к потреблению, предельное изменение количества спроса на товар при изменении дохода потребителя.

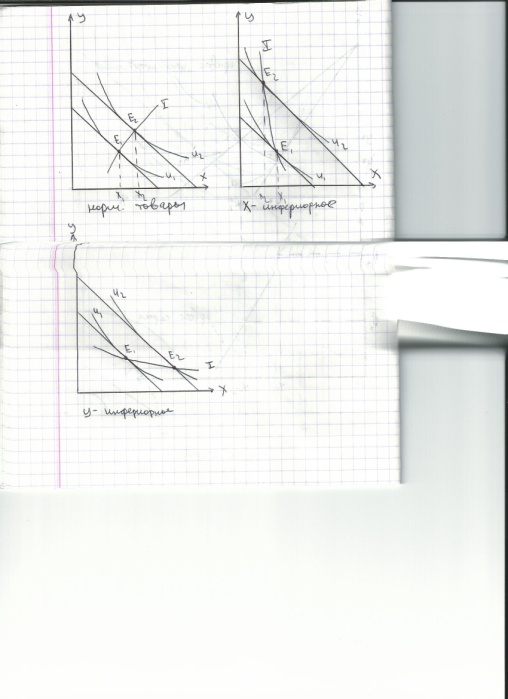
Для инфериорных благ MPC<0, для нормальных товаров MPC>0.

Кривая «доход-потребление» показывает влияние изменения дохода на структуру оптимального набора. Если оба товара нормальные, то кривая имеет полодительный наклон. Если один из товаров инфериорный, то второй непременно нормальный. Кривая Энгеля показывает влияние изменения дохода на потребление отдельного товара. На рисунке – кривые д-п и Энгеля для гомотетичных предпочтений.

Обобщенный закон Энгеля: если в потребительском наборе есть товар с эластичностью спроса по доходу >1, то в нём должен быть товар с эластичностью спроса <1.

Exm*Sm+Eym*Sy=1.

Взвешенная сумма коэффициентов эластичности спроса по доходу равна 1.

5. Эффекты дохода и замещения (прямые и перекрестные) по Е. Слуцкому.

Влияние изменения цены на величину спроса обусловлено двумя видами эффектов: эффектом дохода и эффектом замещения.

Эффект замещения – изменение величины спроса вследствие изменения пропорции обмена между двумя товарами, что побуждает потребителя заменять подорожавший товар на подешевевший.

Эффект дохода – изменение величины спроса вследствие изменения реального дохода потребителя, что побуждает его менять спрос на оба товара.

Как разграничить эффекты? Есть 2 подхода: Е.Слуцкого и Д.Хикса.Различие между ними заключается в трактовке понятия «реальный доход».

«Реальный доход – это кол-во различных благ, которые потребитель может приобрести на свой денежный (номинальный) доход.»

Е.Слуцкий

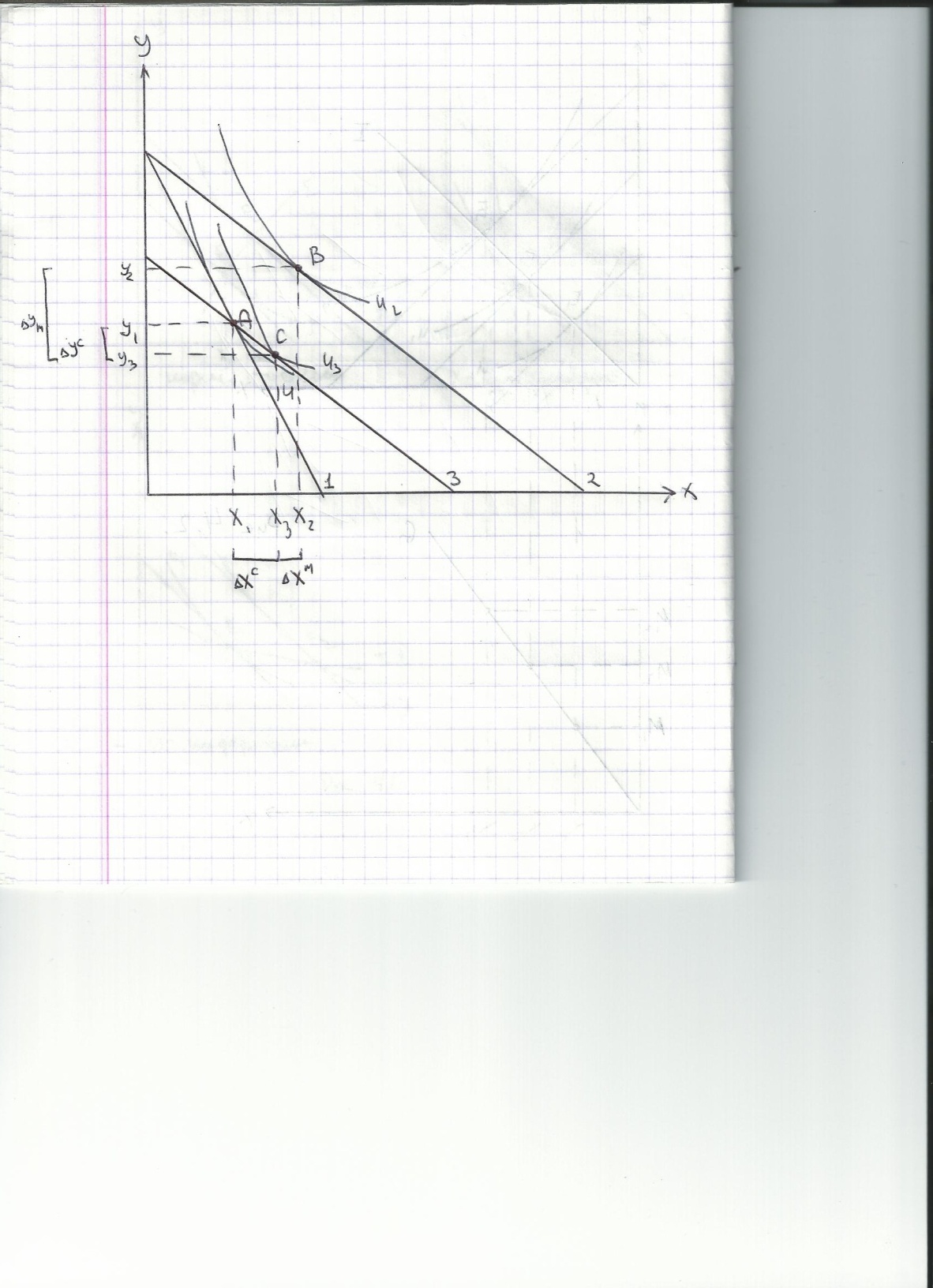Имеется 2 товара. Начальная точка оптимума – А. Пусть цена товара Х понижается. Тогда бюджетная линия становится более пологой, оптимум перемещается. (X2-X1) –общий эффект цены. Для определения эффекта замещения в чистом виде необходимо элиминировать влияние эффекта дохода, т.е. представить, что цены изменились, а доход – нет. Эта предпосылка иллюстрируется вспомогательной линией бюджетного ограничения. Эта линия проходит через точку А, что символизирует факт неизменности реального дохода по Слуцкому. Таким образом, (X3-X1)-эффект замещения (SE), (X2-X3)-эффект дохода (IE).

Для нормальных товаров SE и IE сонаправлены, для инфериорных – SE пер. и IE пер. сонаправлены.

6. Эффекты дохода и замещения (прямые и перекрестные) по Д. Хиксу.

Реальный доход – это уровень полезности, который получает потребитель в результате потребления благ, на которые он истратил свой номинальный доход.

Д.Хикс

Первоначально выбор потребителя характеризуется точкой А. Снижение цены Х приводит к смещению бюджетной линии, этому состоянию соответствует новый оптимум. Вспомогательная линия бюджетного ограничения параллельная бюджетной линии 2, и, следовательно, отражает изменившийся уровень цен. В то же время, она касается первоначальной кривой безразличия, что означает, что новый набор имеет ту же полезность, что и изначальный. Выполняется условие неизменности номинального дохода потребителя по Хиксу.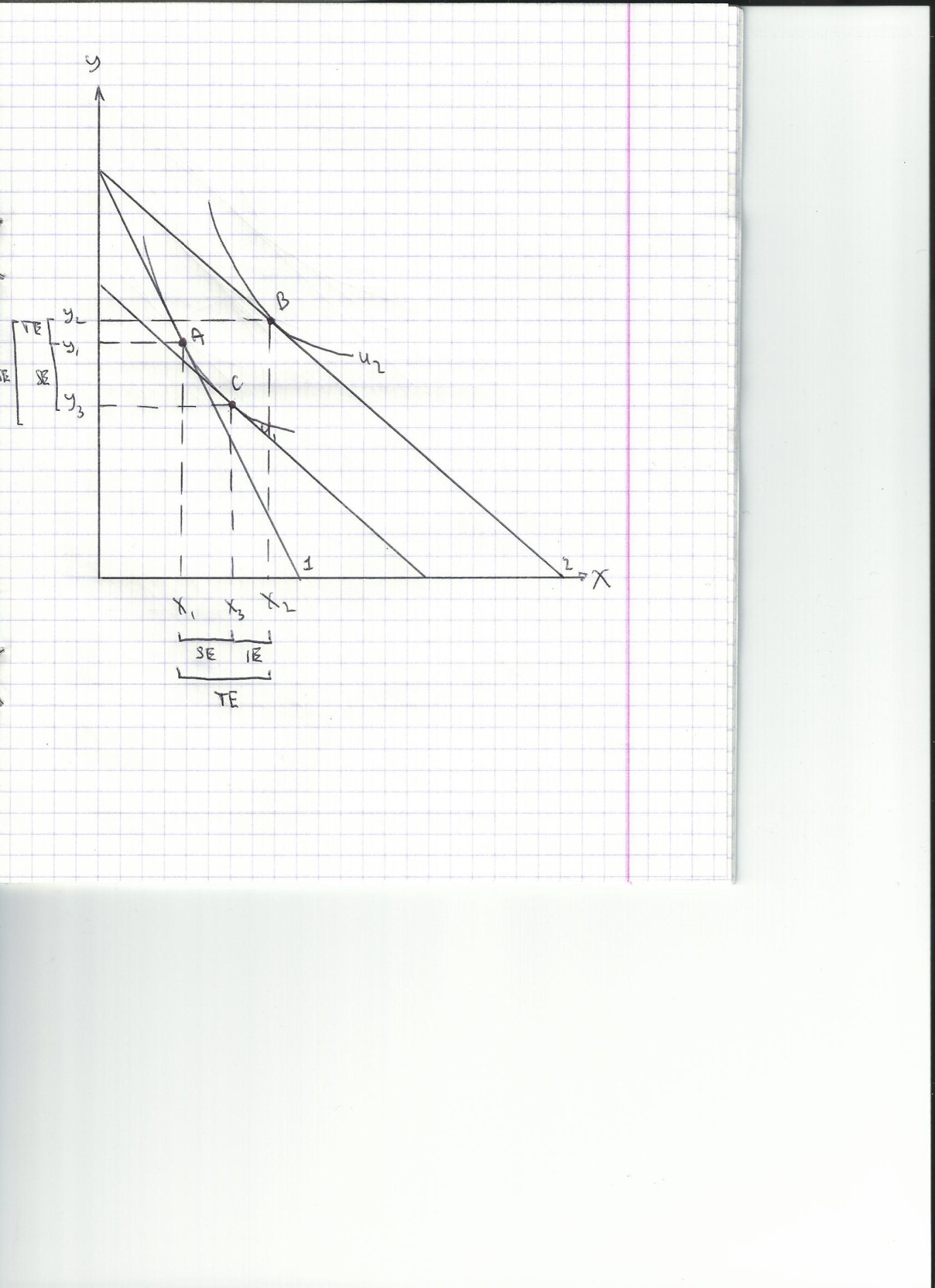

7. Уравнение Е. Слуцкого (в форме относительных изменений, в дифференциальной форме, в коэффициентах эластичности и для перекрестных эффектов).

Для исчисления эффекта дохода и эффекта замещения при изменении цен используется уравнение Слуцкого. Оно отображает тот факт, что общий эффект изменения цены равен алгебраической сумме эффектов дохода и замещения.

TE=SE+IE

8. Компенсирующая и эквивалентная вариации дохода. Компенсированный спрос.

Для того, чтобы выразить в денежной форме изменения чисто полезности, необходимо фиксировать уровень полезности, выражаемый денежной единицей, а для этого следует элиминировать действие эффекта дохода при изменении цены товара. Такое требование соблюдается при использовании компенсирующей и эквивалентной вариаций дохода.

Компенсирующая вариация дает ответ на вопрос: какое изменение в доходе компенсировало бы изменение цен потребителю настолько, чтобы он остался на прежнем уровне благосостояния.

Эквивалентная вариация дает ответ на вопрос: какое изменение в доходе эквивалентно для потребителя данному изменению цен, то есть изменило бы благосостояние агента так же, как оно изменилось из-за изменения цен.

В исходном состоянии оптимум потребителя находится в точке А. Расстояние ОМ – расходы на потребление всех других товаров, если Х=0. Следовательно, (M-Y1)-расзоды на покупку Х. Пусть цена Х выросла. Получаем новый оптимум В. На какую величину следует увеличить номинальный доход, чтобы обеспечить прежний уровень полезности? Увеличиваем доход до касания старой кривой безразличия. Величина (M1-M) – компенсирующая вариация дохода. Какую величину номинального дохода необходимо отбрать у потребителя, чтобы при неизменных ценах снизить его реальный доход в той же степени, в которой снижает его повышение цен? Проводим прямую параллельно первоначальному ограничению (цены не меняются), до касания новой кривой безразличия. (M-M2) – эквивалентная вариация дохода.

Компенсированный спрос

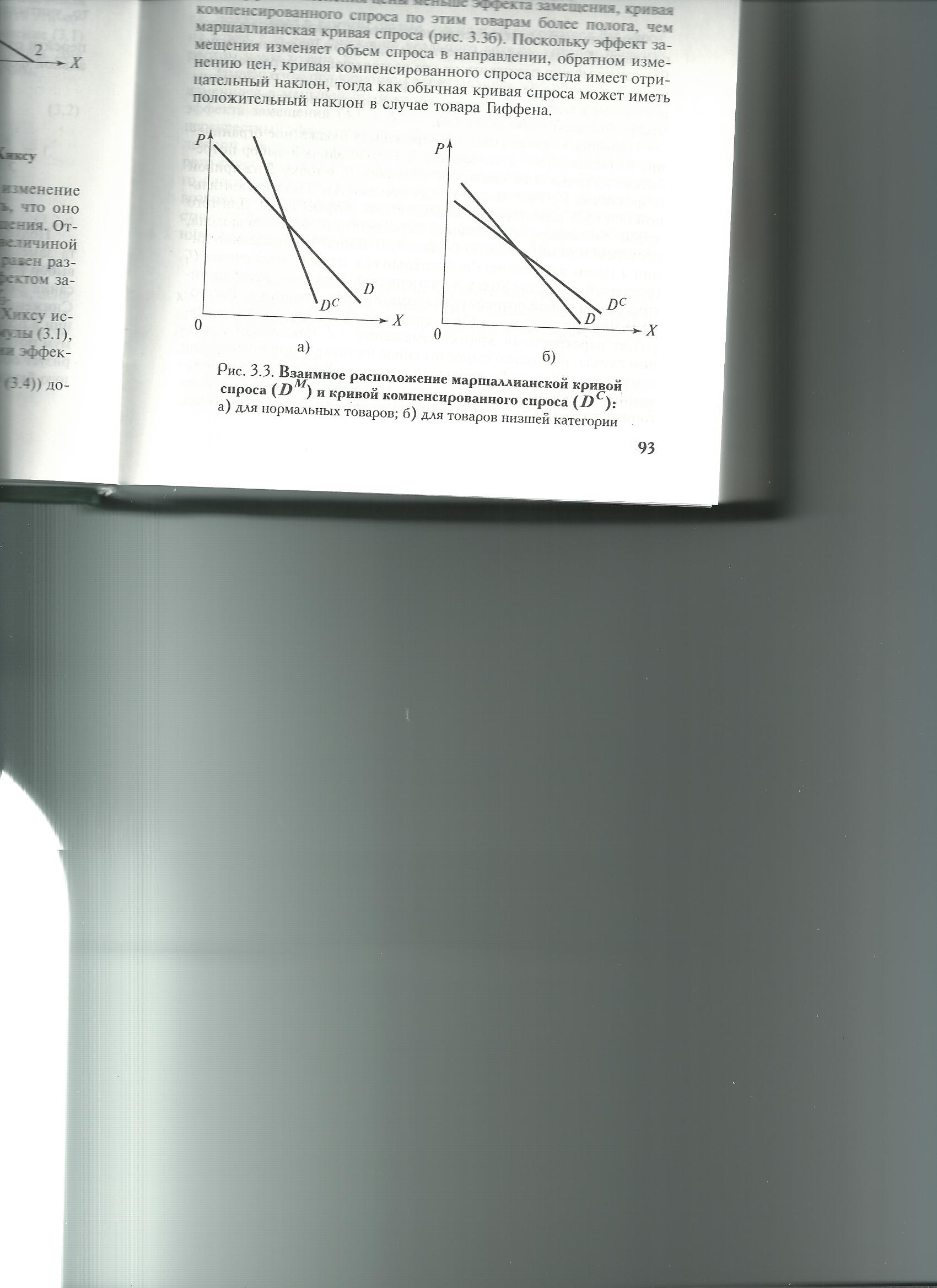Следует различать маршаллианскую кривую спроса и кривую спроса компенсированного. Первая выражает зависимость между ценой и величиной спроса с учетом эффектов и строится при фиксированном номинальном доходе потребителя. Вторая выражает зависимость цены и величины спроса с учетом только эффекта замещения. Поскольку для нормальных товаров общий эффект больше эффекта замещения, кривая компенсированного спроса более крутая. Кривая компенсированного спроса всегда имеет отрицательный наклон. Различают 2 вида кривых компенсированного спроса: кривую Слуцкого и кривую Хикса.

При построении кривой по Слуцкому эффект дохода элиминируется посредством фиксации первоначального набора благ, приобретаемых потребителем. Компенсированный спрос по Слуцкому есть функция от цены товара при доходе, позволяющем приобрести неизменный набор благ.

При построении кривой спроса Хикса эффект дохода элиминируется посредством фиксации первоначального уровня полезности. Компенсированный спрос по Хиксу – функция от цен при неизменном уровне полезности различных наборов благ, приобретаемых потребителем.

9. Излишек потребителя. Взаимосвязь между различными показателями выгоды потребителя.

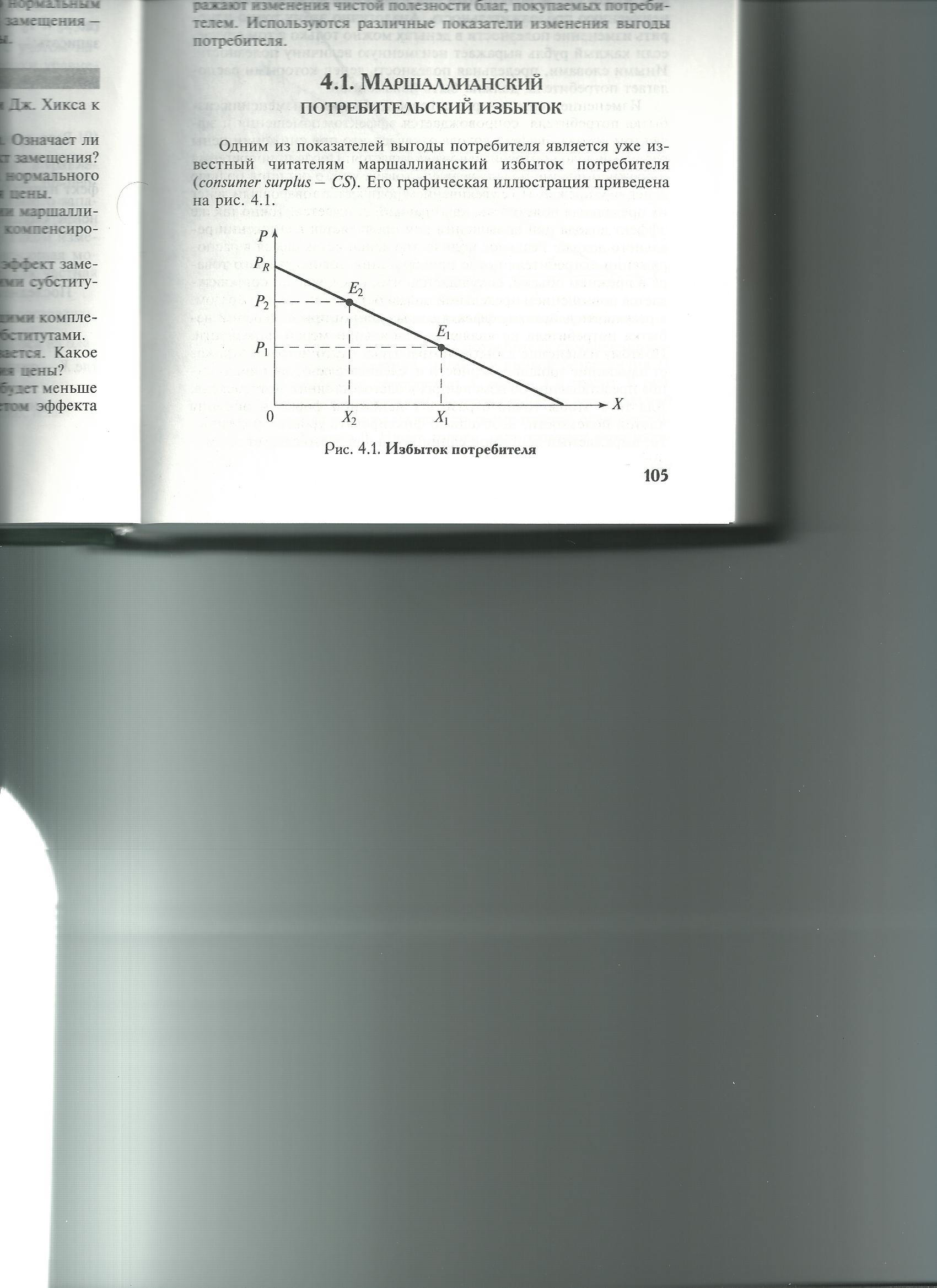Одним из показателей выгоды потребителя является избыток потребителя (CS). Веоичину, соотвествующую площади трапеции PrE1X10 называют общим избытком потребителя. Она характеризует в денежной форме общую полезность, получаемую от потребления Х в объеме Х1.

Разницу между общим избытком потребителя и его затратами на покупку товара Х (P1E1X10), равную площади PrE1X1, называют чистым избытком потребителя, который в денежной форме выражает чистую полезность от потребления товаров, приобретенных по цене Р1. При повышении цена до Р2, СS сокращается на величину, навную площади Р1Р1Е2Е1.

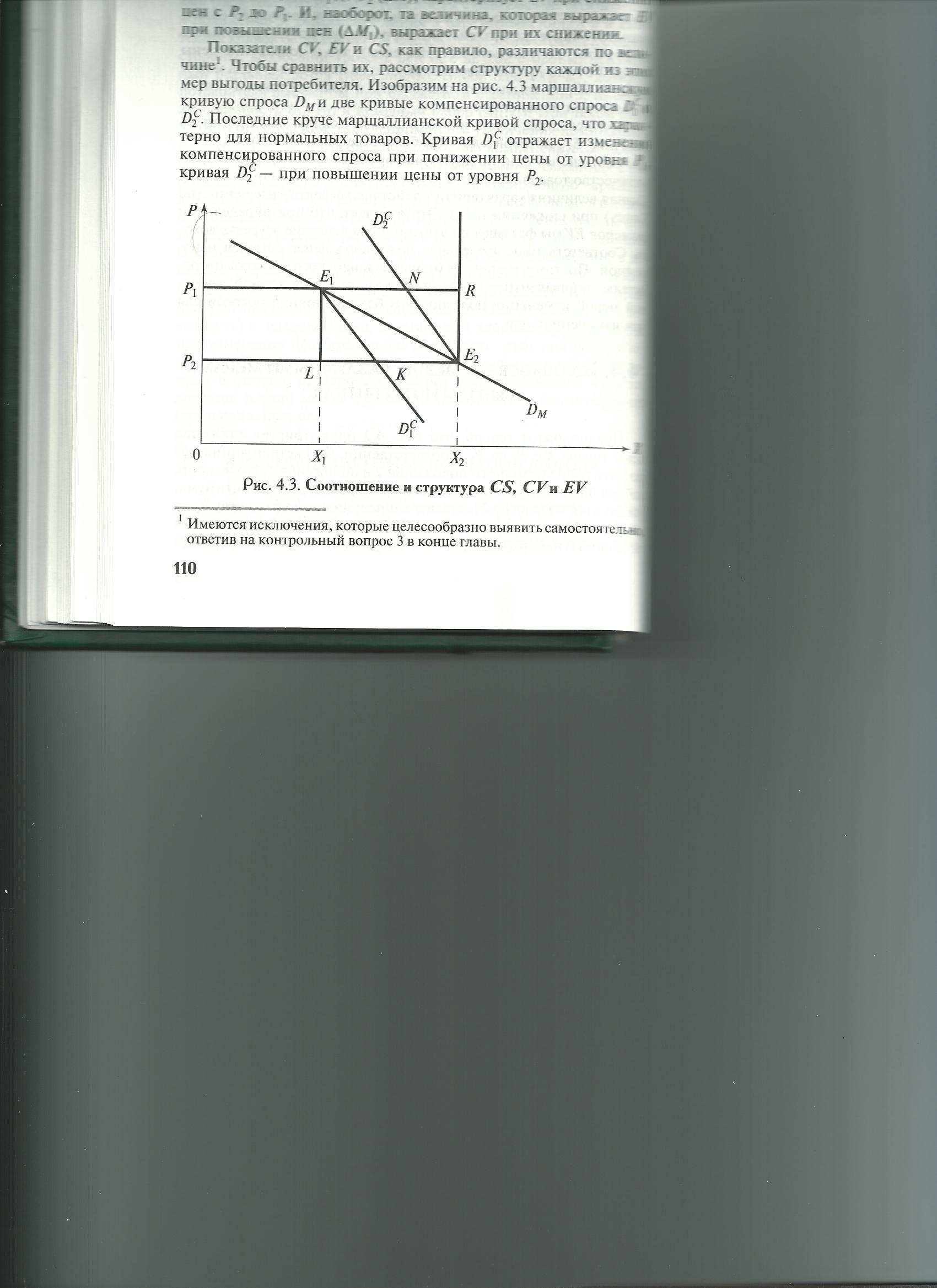Соотношение между различными показателями выгоды потребителя

Та величина, которая характеризует CV при повышении цен с Р1 до Р2, характеризует EV при понижении цен с Р2 до Р1. И наоборот. Это легко доказать, используя график нахождения CV и EV.

Показатели CS, CV и EV обычно различаются по величине. Для сравнения, рассмотрим их струкутуру. На рисунке изображена кривая спроса и две кривые компенсированного спроса (при понижении и повышении цен).

Пусть цена понижается с Р1 до Р2, тогда величина сокращения CS будет представлена площадью P1P2E1E2. Площадь этой трапеции можно разделить на 2 части: прямоугольник Р1Р2E1L (выгода потребителя за счет только изменения цены (чистый эффект цены)) и треугольник LE1E2 (эффект потребления). Треугольник LE1E2 можно разделить на 2 части: LE1K (изменение выгоды за счет эффекта замещения) и KE1E2 (изменение выгоды за счет эффекта дохода). Поскольку при формировании CV действие эффекта дохода не учитывается, можно утверждать, что CV при понижении цены (EV при повышении) соответствует треугольнику Р1Е1КР2.

Пусть цена товара повышается с Р2 до Р1. Тогда влияние на выгоду потребителя эквивалентно площади Р1Р2Е2R. Такие потери понес бы потребитель, если бы продолжил потреблять прежнее количество товара по новой цене. Но количество товара снизилось до Х1. Это снижает потери выгоды от чистого эффекта цены, то есть эффект потребления положителен и равен E1E2R. Разница между эффектом цены и эффектом изменения потребления есть величина изменения CS (Р1Р2Е2Е1). Воздействие эффекта потребления можно разложить на эффект дохода (Е1NЕ2) и эффект замещения (NRЕ2). СV при повышении цены (EV при понижении) соответствует площади P1P2Е2N (эффект дохода не учитывается, CV-сумма позитивного эффекта замещения и негативного эффекта цены).

10. 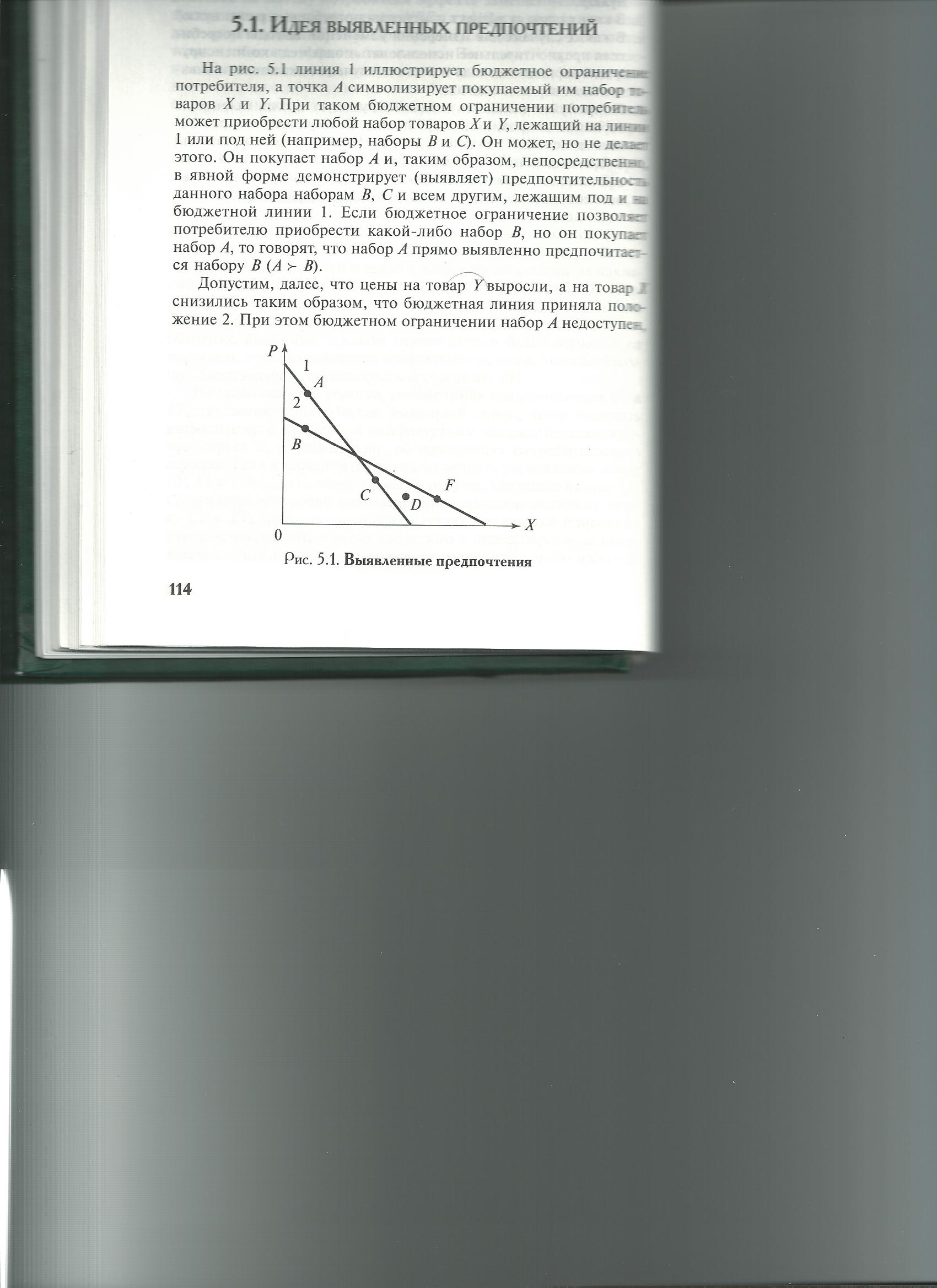Концепция выявленных предпочтений. Роль концепции выявленных предпочтений в теории потребительского выбора. Анализ индексов реального дохода и цен.

На рисунке линия 1 иллюстрирует бюджетное ограничение потребителя, точка А - покупаемый им набор. Потребитель может приобрести любой товарный набор, лежащий на линии 1 или под ней. Но он покупает набор А, демонстрируя предпочтительность его по сравнению с наборами B и С (А>B). Пусть цены на товар У выросли, бюджетная линия сдвинулась в положение 2, и теперь товар А недоступен. Пусть теперь покупается набор В. Можно утверждать, что он прямо выявленно предпочитается наборам F и D. А предпочитается В, следовательно А косвенно (через В) предпочитается F и D.

Концепция выявленный предпочтений базируется на определенной аксиоматике. Выделяют слабую и сильную аксиомы выявленных предпочтений.

Слабая аксиома характеризует прямо выявленное предпочтение. Если потребитель прямо выявлено предпочитает набор А набору В, он не может в то же время прямо выявленно предпочитать набор В набору А. нарушение возможно только если потребитель поступает нерационально, или его вкусы меняются. Другая формулировка аксиомы: если поведение потребителя рационально, его вкусы неизменны и он покупает набор С, когда может купить набор В, то, как бы не менялись цены и доход, он не станет покупать набор В, если ему доступен набор С.

Сильная аксиома выявленных предпочтений характеризует как прямо, так и косвенно выраженные предпочтения. Если потребитель выявленно предпочитает (прямо или косвенно) набор А набору В, то он не может выявленно предпочитать (прямо или косвенно набор В набору А. Эта аксиома вытекает из слабой и аксиомы транзитивности предпочтений. Сильная включает в себя слабую.

Концепция выявленных предпочтений подтверждает выводы теории потребительского выбора. При снижении цен и при прежнем доходе потребитель либо не меняет свой выбор, либо улучшает свое положение. Самые существенные выводы теории потребительского выбора можно получить и без ординалистской функции полезности, которая непосредственно не может быть наблюдаема. Олнако, аналитический аппарат концепции выявленных предпочтений позволяет проводить качественный, но не количественный анализ.

Соединив концепцию выявленных предпочтений и теории. Потребительского выбора, можно вывести кривую безразличия на основе предпочтений.

Практическое значение концепции выявленных предпочтений исчерпывается ее ролью в конкретизации функции полезности. Она имеет собственную роль в оценке изменений благосостояния потребителя.

Для выявления динамики благосостояния потребителей используется индексы номинального и реального дохода и индексы цен. Индексы реального дохода и цен рассчитываются по методикам Ласпейреса или Пааше. В индексах Ласпейреса в качестве весов используются переменные базисного периода, Пааше – отчетного периода.

Выясним. Как используются индексы на практике. Допустим, мы рассматриваем ситуацию, в которой индекс реального дохода Пааше больше 1:

R_p = 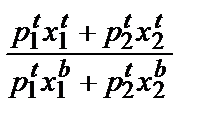> 1.

Перекрестное перемножение частей данного неравенства дает неравенство

+ > + ,

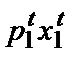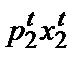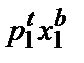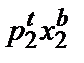которое показывает, что благосостояние потребителя должно быть выше в момент t, нежели в момент b, поскольку в ситуации t он мог бы потребить потребительский набор b, но предпочел не делать этого. Что, если индекс реального дохода Пааше меньше 1? Тогда мы имели бы неравенство 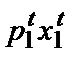+ 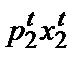< 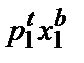+ 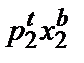, показывающее, что когда потребитель выбрал набор (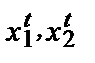), набор (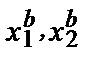) не был ему доступен. Это, однако, ничего не говорит нам о приоритетах потребителя в отношении указанных наборов. Если нечто стоит больше, чем вы можете позволить себе заплатить, это вовсе не означает, что вы предпочитаете это нечто тому, что вы потребляете в настоящий момент. Индекс Пааше < 0 не дает оснований для вывода о снижении благосостояния потребителя.

Индекс Ласпейреса используется аналогичным образом. Предположим, что индекс реального дохода Ласпейреса меньше 1:

R_L = 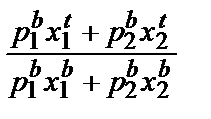.< 1.

Перекрестное умножение даст нам неравенство

+ < + ,

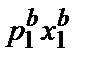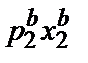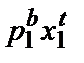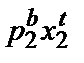говорящее о том, что (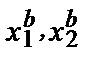) выявленно предпочитается (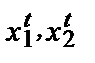). Таким образом, благосостояние потребителя выше в момент b, чем в момент t.

Индексы цен используются примерно таким же образом. Вообще, индекс цен — это взвешенная средняя цен:

I_p = .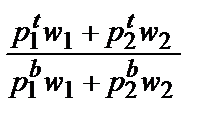

В этом случае естественно выбрать в качестве весов для расчета средние количества товаров. Мы получим два разных индекса в зависимости от того, что выбрать в качестве весов. Если весами выбраны количества товаров в период t, мы получаем индекс цен Пааше:

P_p = ,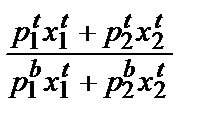

а если весами выбраны количества товаров базисного периода, получаем индекс цен Ласпейреса:

L_p = .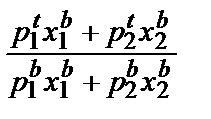

Предположим, что индекс цен Пааше меньше 1. Выявленные предпочтения не говорят об этом ничего. Проблема заключается в том, что теперь в числителе и в знаменателе дробей, образующих индексы, стоят разные цены, так что сравнение с позиций выявленных предпочтений произвести невозможно.

Введем новый индекс изменения общих расходов (именуемый также индексом номинального дохода), определив его как

M = .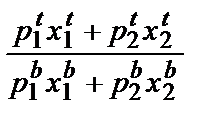

Это отношение общих расходов периода t к общим расходам периода b.

Допустим теперь, что индекс цен Пааше больше M. Это означает, что

P_p = > .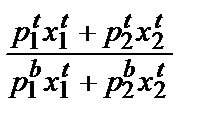

+ > + .

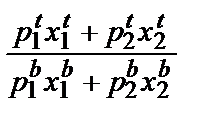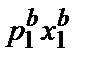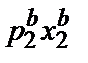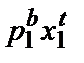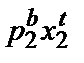Это неравенство говорит о том, что набор, выбранный в году b, выявленно предпочитается набору, выбранному в году t. Из данного анализа следует, что если индекс цен Пааше больше индекса номинального дохода, то благосостояние потребителя должно быть выше в году b, чем в году t. Аналогичное утверждение можно сделать и в отношении индекса цен Ласпейреса. Если индекс цен Ласпейреса меньше M, то благосостояние потребителя в году t должно быть выше, чем в году b. В случае индексов цен важно не то, больше или меньше данный индекс единицы, а то, больше он или меньше индекса номинального дохода.

11. Потребительский выбор с учетом начального запаса. Уравнение Е. Слуцкого с учетом начального запаса.

Начальный запас – это то количество благ, которое потребитель имеет еще до начала анализа в жестко фиксированном виде. Е0(Х0,У0) – начальный запас до выхода на рынок

Е1(Х1,У1) – фактический потребляемый набор товаров Х и У после возвращения с рынка.

(Х1-Х0) и (У1-У0) – чистый спрос на Х и У.

Если чистый спрос < 0, то потребитель – чистый продавец, если чистый спрос > 0, то потребитель – чистый покупатель.

Налицо два противоположных эффекта дохода. Один – стандартный (при повышении цен потребитель теряет часть дохода, при понижении – становится богаче), а второй – нетрадиционный, связанный с наличием начального запаса (при повышении цен производитель становится богаче, при понижении – беднее). Этот вид эффекта называется эффект начального запаса.

Точка А на рисунке характеризует начальный запас, В – оптимальный набор. Индивид явля 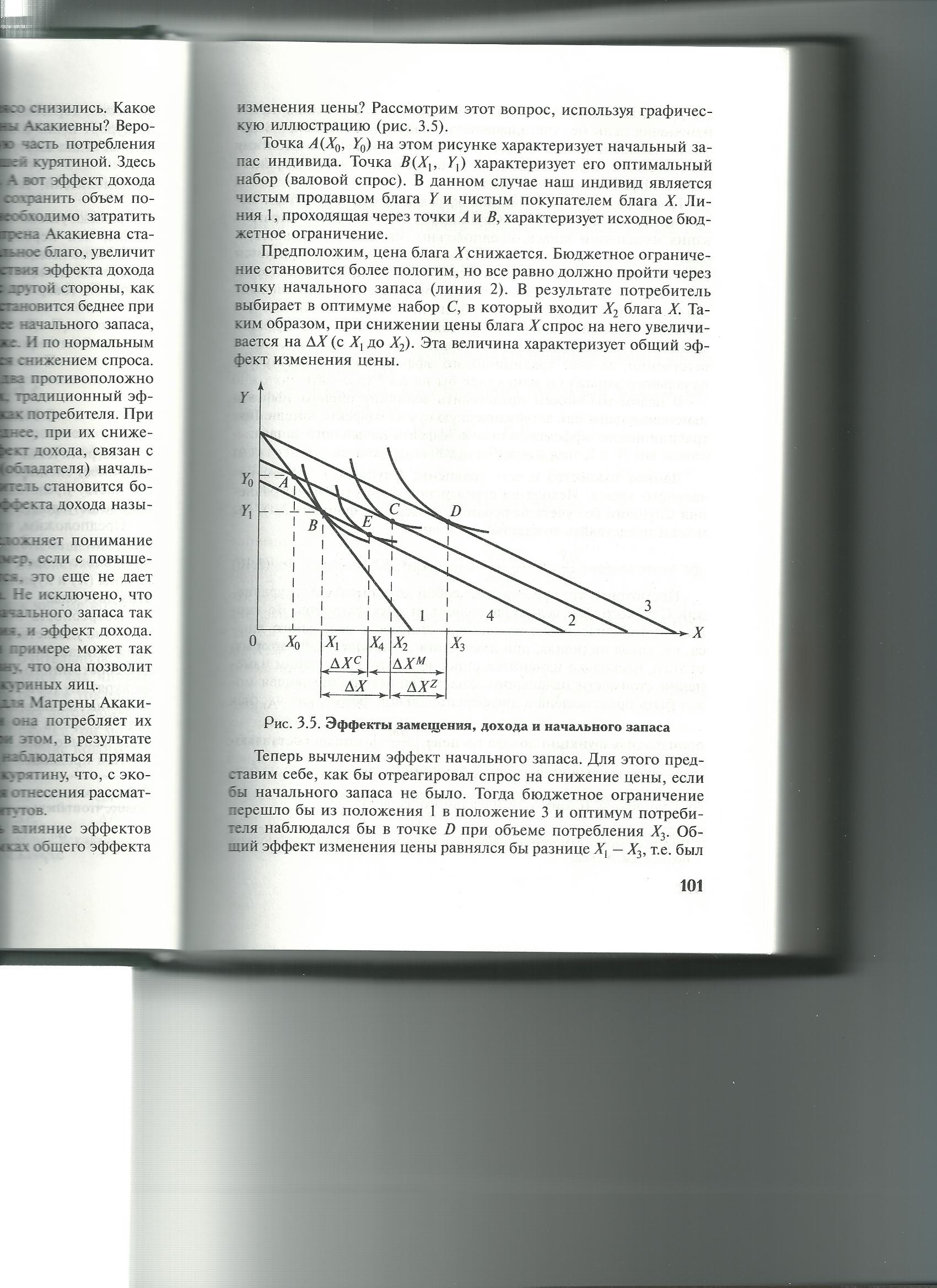ется чистым продавцом блага У и покупателем блага Х.

Пусть цена Х снижается, тогда бюджетное ограничение становится более пологим, но все равно должно пройти через точку начального запаса. Потребитель выбирает набор С. (Х2-Х1) – общий эффект цены. Вычленим эффект начального запаса. Представим, как отреагировал бы спрос, если бы запаса не было. Ограничение перешло бы в линию 3, оптимум – в точку D. Общий эффект был бы равен (Х3-Х1). Значит, (Х3-Х2) – эффект начального запаса.

Общий эффект равен сумме эффектов запаса, дохода и замещения.

Величина последнего компонента зависит от 2-х факторов: насколько изменилась стоимость начального запаса и от того, насколько изменился спрос на товар Х. Первая составляющая определяется как производная функции дохода по цене, вторая – как частная производная функции валового спроса по доходу. В целом эффект начального запаса имеет вид:

Поскольку доход, представленный начальным запасом, выражается как М=РхХ0+РуУ0, можно записать:

Уравнение Слуцкого принимает вид:

Известно, что эффект замещения всегда имеет отрицательный знак — противоположный направлению изменения цены. Предположим, что товар нормальный. Тогда знак совокупного эффекта дохода зависит от того, является ли данный индивид чистым покупателем или чистым продавцом рассматриваемого товара. Если данный индивид — чистый покупатель нормального товара и цена этого товара растет, то потребитель, безусловно, купит его меньше. Если потребитель — чистый продавец нормального товара, то знак совокупного эффекта дохода неопределенный: он зависит от величины (положительной) совокупного эффекта дохода, сопоставленной с величиной (отрицательной) эффекта замещения.

12. Распределение потребления между настоящим и будущим периодами: бюджетное ограничение, карта кривых безразличия и оптимум потребителя. Влияние ограничений по заимствованию и изменений дохода на оптимум потребителя при межвременном выборе.

см. конец файла

13. Влияние изменений ставки процента на оптимум потребителя при межвременном выборе. Эффект дохода, эффект случайного заработка и общий эффект изменения процентной ставки для кредитора и заемщика. Сбережения и уровень ставки процента.

см. конец файла

14. Производственная функция. Предельная норма технического замещения. Эластичность замещения. Производственная функция и технический прогресс.

Вводимые в производство ресурсы называются факторами производства. Они часто подразделяются на крупные категории, такие, как земля, труд, капитал и сырьевые материалы. Будем считать, что вводимые ресурсы и выпуск измеряются единицами потока: определенное количество труда в неделю и определенное число часов работы машин в неделю производят определенную величину выпуска в неделю.

Природа налагает на фирмы технологические ограничения: лишь некоторые комбинации вводимых ресурсов представляют собой практически осуществимые способы производства данного объема выпуска, и фирма должна ограничивать свой выбор технологически выполнимыми производственными программами. Простейший способ описания выполнимых производственных программ — это составление их перечня. Иными словами, мы можем составить список всех комбинаций вводимых ресурсов и выпусков, являющихся технологически достижимыми. Множество всех комбинаций вводимых ресурсов и выпусков, которые охватывают технологически достижимый способ производства, называется производственным множеством. Предположим, например, что у нас имеется только один вводимый ресурс, в количестве x, и только один выпуск, в количестве y. Тогда производственное множество может иметь форму, показанную на рисунке. Утверждение, что некоторая точка (x, y) принадлежит производственному множеству, означает просто следующее утверждение: имея количество x данного вводимого ресурса, технологически возможно произвести выпуск в объеме y. Производственное множество показывает возможные для данной фирмы варианты технологического выбора. Поскольку фирма оплачивает вводимые ресурсы, имеет смысл ограничиться изучением максимально возможного выпуска при данном уровне вводимого ресурса. Это — граница производственного множества, представленного на рис.17.1. Функция, описывающая границу этого множества, известна как производственная функция. Она показывает максимально возможный выпуск, который может быть получен из данного количества вводимого ресурса. Разумеется, концепция производственной функции в равной степени применима и тогда, когда имеется несколько вводимых ресурсов. Если, например, мы рассматриваем случай двух вводимых ресурсов, производственная функция f(x₁, x₂)будет показывать максимальный объем выпуска y, который мы могли бы получить, если бы у нас имелось x₁ единиц фактора 1 и x₂единиц фактора 2. Существует удобный способ изображения производственных взаимосвязей для случая двух факторов производства, известный как изокванта.

Изокванта — это множество всех возможных комбинаций факторов 1 и 2, которые как раз достаточны для производства данного объема выпуска.

Изокванты подобны кривым безразличия. Но при этом изокванты обозначаются не уровнями полезности, а объемами выпуска, которые могут быть произведены с помощью соответствующих комбинаций факторов. Поэтому обозначение изоквант задано технологией и не имеет той произвольной природы, которая присуща обозначению полезности.

Предположим, что мы производим в некоторой точке (x₁, x₂) и раздумываем, не стоит ли отказаться от небольшого количества фактора 1, добавив при этом как раз столько фактора 2, сколько потребуется, чтобы произвести тот же самый объем выпуска y. Сколько нам потребуется дополнительно фактора 2 x₂, если мы собираемся отказаться от небольшого количества фактора 1 x₁? Это отношение представляет собой как раз наклон изокванты; мы называем его технологической нормой замещения (МTRS) и обозначаем МTRS(x₁, x₂).

Технологическая норма замещения показывает выбор между двумя факторами в производстве. Она измеряет пропорцию, в которой фирме придется заместить один фактор другим, чтобы оставить выпуск без изменений.

Чтобы вывести формулу для МTRS, можно воспользоваться той же самой идеей, что и при определении наклона кривой безразличия. Рассмотрим такое изменение используемых количеств факторов 1 и 2, при котором выпуск остается постоянным. Для этого возьмем полный дифференциал производственной функции y=f(x₁, x₂). Тогда мы имеем уравнение

dy = MP₁(x₁, x₂) dx₁ + MP₂(x₁, x₂) dx₂ = 0, где дифференциалы независимых переменных есть их соответствующие приращения.

В результате решения уравнения получаем

МTRS(x₁, x₂) = = — .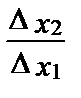

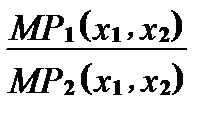Эластичность замещения показывает, на сколько процентов изменится отношение факторов (капитала к труду) при изменении предельной нормы замещения на 1%. Математически это выражается так:

E₁₂=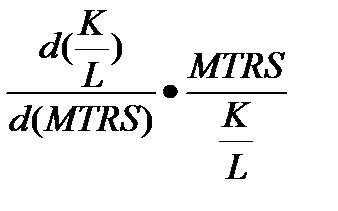

Важно отметить, что неважно, какую именно эластичность замены считать. Эластичность замены первого фактора вторым и эластичность замены второго фактора первым равны.

В результате технического прогресса возможен рост производства, который заключается в появлении новых, технически более эффективных способов производства. Эти новые способы должны быть учтены в производственной функции, тогда как старые должны быть исключены из нее. Графически технический прогресс может быть отражен сдвигом вниз изокванты и, возможно, изменением ее конфигурации. Сдвинутая вниз изокванта характеризует тот же объем выпуска, что и старая, но теперь этот объем выпуска может быть достигнут за счет применения меньшего количества капитала и труда. Сдвиг изокванты может сопровождаться изменением ее конфигурации, что означает изменение соотношения применяемых ресурсов. В связи с этим различают три типа технического прогресса: капиталоинтенсивный (трудосберегающий), трудоинтенсивный (капиталосберегающий) и нейтральный. Технический прогресс называется капиталоинтенсивным, если при движении вдоль линии с постоянным соотношением К/L, предельная норма замещения одного фактора другим снижается. Это означает, что технический прогресс сопровождается опережающим ростом предельного продукта капитала по сравнению с трудом. Трудоинтенсивный технический прогресс сопровождается опережающим ростом предельного продукта труда по сравнению с предельным продуктом капитала. Наклон изокванты при приближении к началу координат становится все более пологим относительно оси К. Наконец, нейтральным называется технический прогресс, в результате которого происходит пропорциональное увеличение обоих факторов, но предельная норма замещения остается неизменной. Не меняется при этом и наклон изокванты, под воздействием технического прогресса она смещается параллельно самой себе.

15. Принцип минимизации издержек. Концепция выявленной минимизации издержек.

Различают капитальные и текущие издержки производста. Капитальные издержки – это затраты на приобретение или создание основного капитала, потребляемого постепенно. Текущие издержки – затраты на ресурсы, потребляемые в течение какого-либо промежутка времени.

Бухгалтерские издержки включают только те выплаты и начисления, которые должны быть учтены в соответствии с законодательными актами о бухгалтерском учете. Экономические издержки включают все явные издержки, т.е. все платежи, которые необходимо осуществить для производства и реализации продукции. Если производственная необходимость требует осуществления каких-либо неофициальных выплат, то они не могут быть отражены в бухгалтерской отчетности, но должны быть включены в экономические издержки. В отличие от бухгалтерских экономические издержки включают не только явные, но и неявные издержки, т.е. платежи, условно начисляемые за все ресурсы, которые принадлежат собственникам фирмы.

Пусть r-арендная плата за час работы капитала, w-часовая ставка оплаты труда. Общие издержки выпуска выражаются как

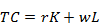или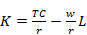

Зависимость издержек и количества ресурсов можно представить линиями, которые называются изокосты. Величина наклона изокост равна 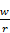. Минимизация издержек сводится к уравнению MRTS(L,K)=w/r.

Норма замещения ресурсов в производстве должна быть равна отношению, в котором они могут быть замещены на рынке.

MP(L)/w=MP(K)/r.

Все способы производства, лежащие на изокванте являются технологически эффективными, но экономическая эффетивность достигается только в одном случае, когда минимальны издержки производства. Можно решать эту задачу другим способом, выбирая максимальный выпуск при данных издержках.

Аксиома минимизации издержек (Weak Axiom of Cost Minimization WACM): если фирма минимизирует издержки на определенный объем производства, то они должны быть по крайне мере не выше того уровня, который сложился бы при данных ценах при использовании другого способа производства.

r1K1+w1L1£r1K2+w1L2

r2K2+w2L2£r2K1+w2L1

Запишем второе неравенство в виде

-r2K1-w2L1 £ -r2K2-w2L2

и прибавим его к первому неравенству и вынесем общие члены, получив при этом неравенство

(r1-r2)(K1-K2)+(w1-w2)(L1-L2) £0

∆r∆K+∆w∆L£0

Это неравенство позволяет дать первичную оценку деятельности фирмы. Если оно не соблюдается, то аксиома минимизации издержек нарушена.

16. Экономически эффективные способы производства. Траектория расширения производства и условный спрос на ресурсы.

Пусть минимизирующая издержки фирма увеличивает выпуск. Она переходит на более высокие изокванты, используя экономически эффективные способы производства.

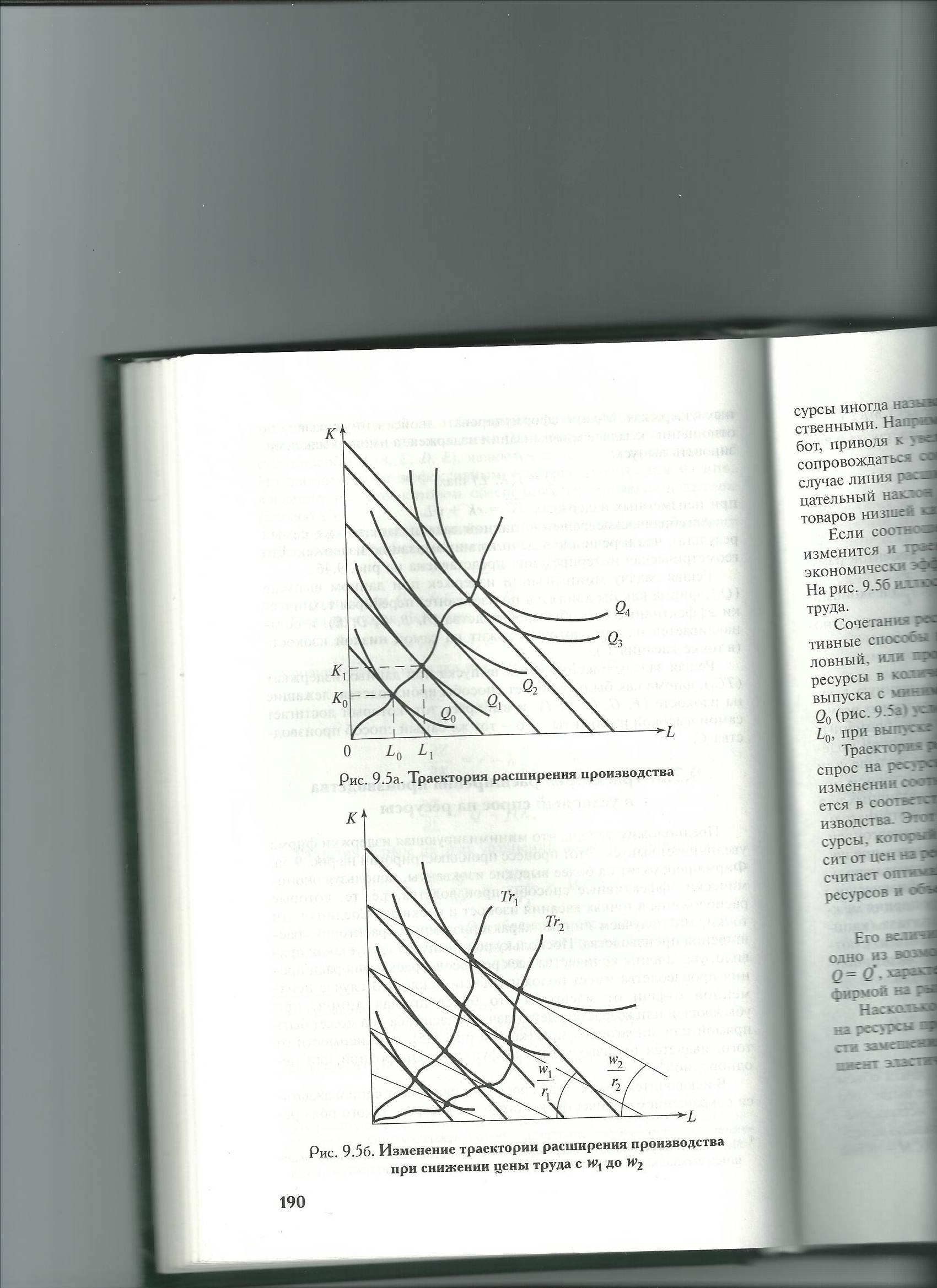Экономически эффективными способами производства являются такие конфигурации ресурсов, при которых изокванта и изокоста касаются, и точка касания является в задаче максимизации выпуска Q=f(K,L) при заданном ограничении на ресурсы (С=rK+wL) точкой максимума целевой функции Q=f(K,L), а в задаче минимизации издержек (С=rK+wL) при заданном объеме выпуска Q=f(K,L) она является точкой минимума. Соединяя точки касания изоквант и изокост, мы получаем линию, характеризующую траекторию расширения производства. Поскольку рост выпуска требует увеличения количества всех ресурсов, траектория расширения производства имеет положительный наклон. В случае неизменной отдачи от масштаба это будет прямая линия, при убывающей отдаче или возрастающей отдаче она может быть прямой или зигзагообразной, в зависимости от того, является производственная функция однородной или неоднородной. Если соотношение цен факторов производства изменится, изменится и траектория расширения производства, поскольку экономически эффективными станут иные способы производства. Сочетания ресурсов, характеризующие экономически эффективные способы производства, формируют условный, или производный, спрос на ресурсы. Это спрос на ресурсы, необходимые для определенного объема выпуска с минимальными издержками. Траектория расширения производства характеризует условный спрос на ресурсы во всех возможных значениях выпуска. При изменении соотношения цен на ресурсы условный спрос изменяется в соответствии с изменением траектории расширения производства. Условный спрос есть функция от цен ресурсов и объема выпуска: D(усл)=f(r,w,Q).

Насколько интенсивными будут изменения условного спроса на ресурсы при изменениях цен на ресурсы, зависит от эластичности замещения:

(*)

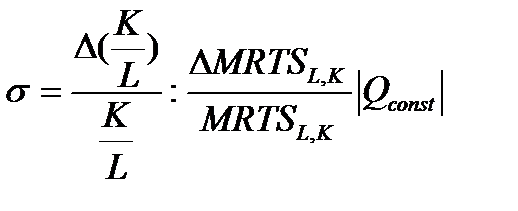Поскольку в точке оптимума (минимум издержек) MRTS= 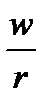, коэффициент эластичности замещения можно представить в виде * только с заменой MRTS на w/r. Коэффициент показывает, на сколько процентов изменится капиталовооруженность труда в экономически эффективном способе производства при изменении отношения цен на ресурсы (w/r) на 1%.

17. Взаимосвязь между краткосрочными и долгосрочными издержками.

В проведенном выше анализе мы рассматривали в качестве постоянных издержек фирмы издержки, связанные с оплатой факторов, не подлежащих изменению в краткосрочном периоде. В длительном периоде фирма может выбирать количество используемых ею "постоянных" факторов — они более уже не являются постоянными.

Разумеется, в длительном периоде по-прежнему могут иметься квазипостоянные факторы. Иными словами, данная технология может обладать тем свойством, что некоторые издержки придется оплачивать, чтобы произвести любой положительный объем выпуска. Однако в длительном периоде не существует постоянных издержек в том смысле, что всегда есть возможность произвести ноль единиц выпуска при нулевых издержках, иными словами, всегда существует возможность прекратить деятельность. Если в длительном периоде имеются квазипостоянные факторы, то кривая средних издержек будет иметь, как и в коротком периоде, U-образную форму. Но в длительном периоде, по самому его определению, всегда будет существовать возможность производства нулевого выпуска при нулевых издержках. Конечно, какой именно период следует считать длительным, зависит от исследуемой задачи. Если в качестве постоянного фактора мы рассматриваем размеры завода (здесь и далее под размером завода понимаются производственные мощности), то продолжительность длительного периода будет определяться тем, сколько времени потребуется фирме, чтобы изменить размеры своего завода. Если мы рассматриваем в качестве постоянного фактора контрактные обязательства по выплате заработной платы, то продолжительность длительного периода будет зависеть от того, сколько времени потребуется фирме, чтобы изменить количество используемой ею рабочей силы. Чтобы быть конкретнее, будем считать постоянным фактором размер завода и обозначим его размер буквой k. Функцию краткосрочных издержек фирмы при условии, что фирма имеет завод площадью k квадратных футов, обозначим через c_s(y, k), где нижний индекс s обозначает "краткосрочный период" (k здесь играет такую же роль, какую в гл. 19 играет ). Для любого данного объема выпуска всегда существует какой-то размер завода, который оптимален для производства этого объема выпуска. Обозначим этот размер завода через k(y). Это условный спрос фирмы на фактор (в роли которого выступает размер завода) как функция выпуска. (Разумеется, он также зависит от цены размера завода и от цен других факторов производства, но эти аспекты аргументации мы оставляем в стороне). Тогда, как мы видели в гл. 19, функция долгосрочных издержек фирмы будет задана выражением c_s(y, k(y)). Это общие издержки производства объема выпуска y при условии, что фирма имеет возможность оптимально изменять размеры своего завода. Функция долгосрочных издержек фирмы есть не что иное, как функция ее краткосрочных издержек, оцененная в точке оптимального выбора постоянных факторов:

c(y) = c_s(y, k(y)).

Посмотрим, как это выглядит на графике. Выберем какой-то объем выпуска y*и обозначим через k* = k(y*)оптимальный размер завода для данного объема выпуска. Функция краткосрочных издержек для завода размером k*задается выражением c_s(y, k*), а функция долгосрочных издержек — выражением c(y) = c_s(y, k(y)), как показано выше. Теперь обратите внимание на тот важный факт, что краткосрочные издержки производства выпуска y должны всегда быть по крайней мере не меньше, чем долгосрочные издержки производства y. Почему? В краткосрочном периоде размер завода фирмы постоянен, в то время как в долгосрочном периоде фирма вольна изменять размер своего завода. Поскольку одним из возможных вариантов выбора фирмы в длительном периоде является выбор завода размером k*, оптимальному выбору производства y единиц выпуска должны соответствовать издержки по крайней мере не большие, чем c(y, k*). Это означает, что при изменении размера завода дела фирмы должны идти по крайней мере не хуже, чем при постоянном размере завода. Поэтому

c(y) £ c_s(y, k*) для всех объемов выпуска y.

На самом деле мы знаем, что для одного конкретного объема y, а именно для y*,

c(y*) = c_s(y*, k*).

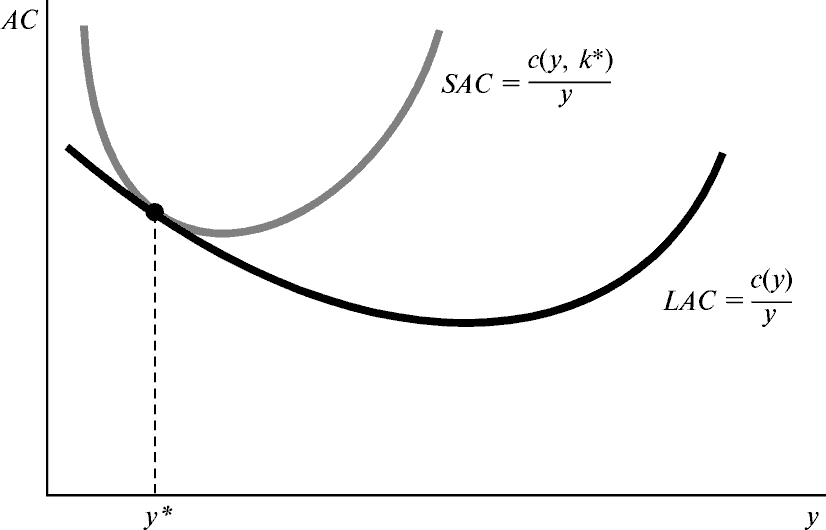Почему это так? Потому что при y*оптимальным выбором размера завода является k*. Поэтому при y*долгосрочные и краткосрочные издержки производства оказываются одинаковыми.

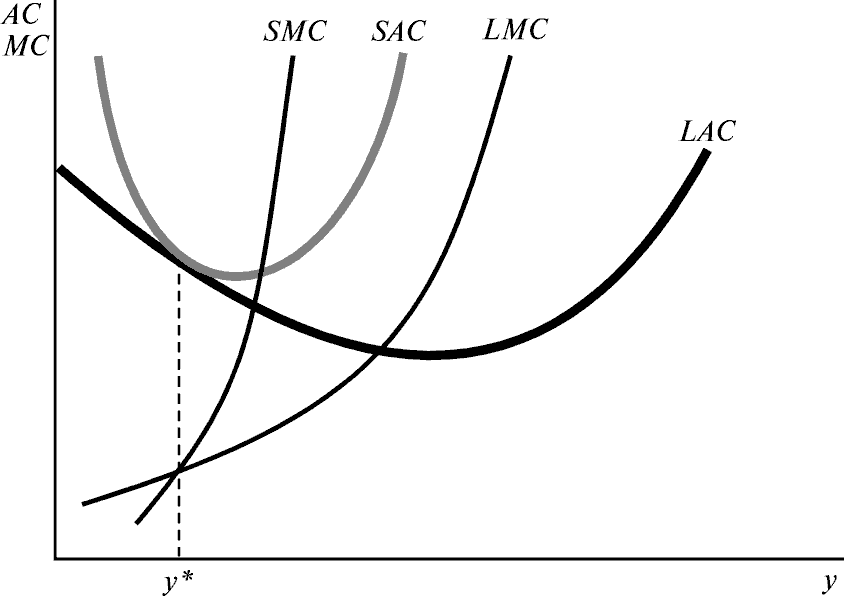
Если краткосрочные издержки всегда больше долгосрочных и они равны при равном объеме выпуска, это означает, что краткосрочные и долгосрочные издержки обладают одним и тем же свойством: AC(y) £ AC_s(y, k*)и AC(y*) = AC_s(y*, k*). Это подразумевает, что кривая краткосрочных средних издержек всегда лежит над кривой долгосрочных средних издержек и они касаются друг друга в одной точке y*. Поэтому кривая долгосрочных средних издержек (LAC) и кривая краткосрочных средних издержек (SAC) в этой точке должны касаться друг друга, как показано на рисунке.

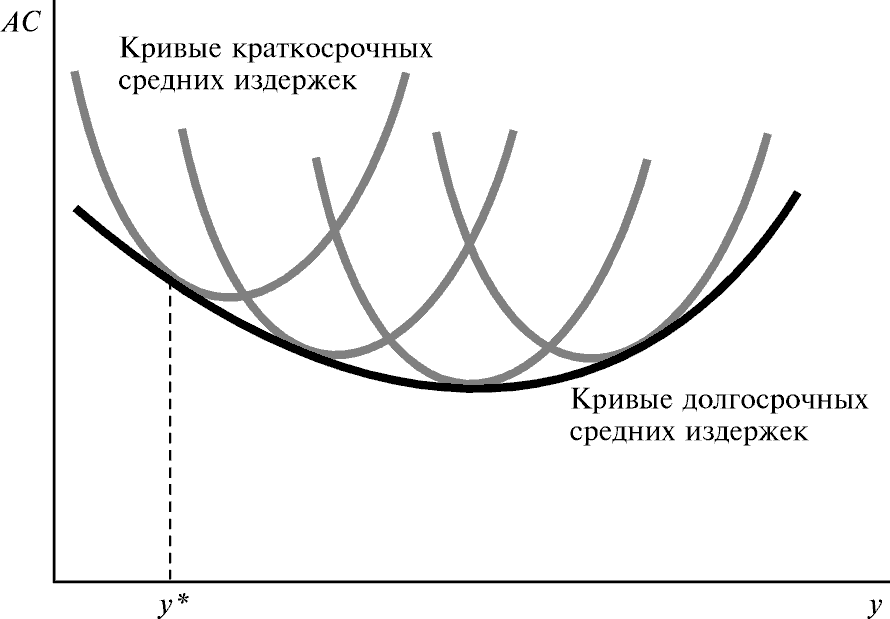Мы можем проделать такого же рода построения для объемов выпуска, отличных от y*. Предположим, что мы выбираем объемы выпуска y₁, y₂,..., y_n и соответствующие им размеры завода k₁ = k(y₁), k₂ = k(y₂),..., k_n = k(y_n). Тогда получаем картину, подобную изображенной на рисунке. Суть заключается в утверждении, что кривая долгосрочных средних издержек огибает кривые краткосрочных средних издержек снизу.

Допустим, например, что имеются четыре различных варианта выбора размера завода, k₁, k₂, k₃и k₄. На рис.20.8 изображены четыре различные кривые средних издержек, соответствующих этим размерам завода.

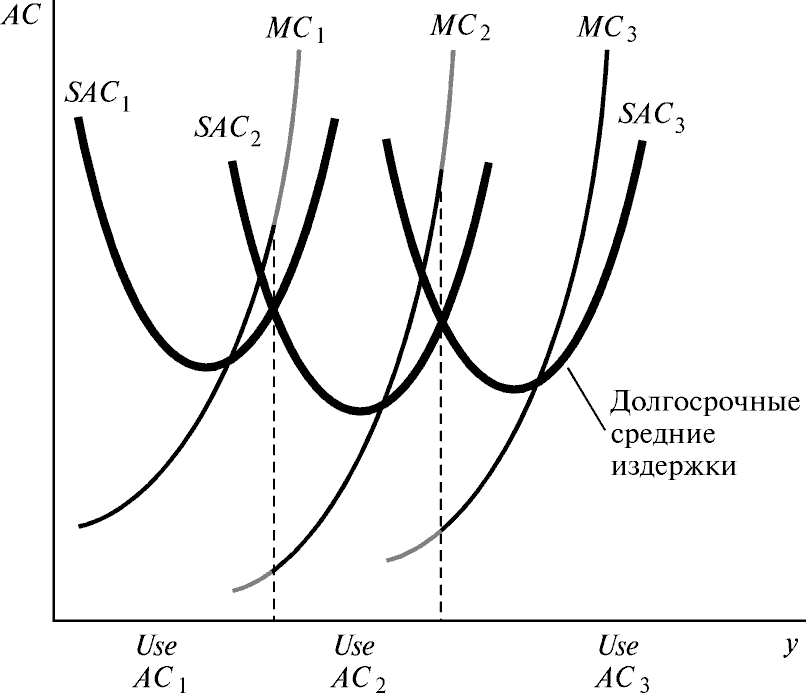
Как можно построить кривую долгосрочных издержек? Вспомним, что кривая долгосрочных средних издержек есть та кривая издержек, которую мы получаем, оптимально изменяя k. В данном случае сделать это нетрудно: поскольку у нас всего четыре различных размера завода, мы просто смотрим, какому из них соответствуют наименьшие издержки, и выбираем именно этот размер завода. Иными словами, для любого объема выпуска y мы просто выбираем такой размер завода, который дает минимальные издержки производства данного объема выпуска. Таким образом, кривая долгосрочных средних издержек должна, как показано на рис.20.8, являться нижней огибающей кривых краткосрочных средних издержек. Обратите внимание на то, что качественный смысл этого рисунка тот же самый, что и рис.20.7: краткосрочные средние издержки всегда по крайней мере не меньше долгосрочных средних издержек, и указанные издержки равны при том объеме выпуска, при котором долгосрочный спрос на постоянный фактор равен имеющемуся у вас количеству постоянного фактора.

Как мы видели в предыдущем параграфе, кривая долгосрочных средних издержек есть нижняя огибающая кривых краткосрочных средних издержек. Что из этого следует применительно к предельным издержкам? Вначале рассмотрим случай с дискретными размерами завода. В этой ситуации кривая долгосрочных предельных издержек состоит, как показано на рис.20.9, из соответствующих кусков кривых краткосрочных предельных издержек. При каждом объеме выпуска мы смотрим, в соответствии с какой кривой краткосрочных средних издержек мы производим, а затем на то, какие предельные издержки связываются с данной кривой.

Это должно быть верно независимо от того, сколько у нас имеется различных размеров завода, так что в случае их непрерывного количества получаем картину, подобную изображенной на рис.20.10. Долгосрочные предельные издержки при любом объеме выпуска y должны равняться краткосрочным предельным издержкам, связанным с размером завода, оптимальным для производства выпуска y.

18. Максимизация прибыли и спрос на ресурсы. Линии изоприбыли. Концепция выявленной максимизации прибыли.

Рассмотрим задачу максимизации прибыли в коротком периоде, когда фактор 2 фиксирован на некотором уровне 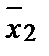. Пусть f(x₁, x₂)— производственная функция фирмы, p — цена выпуска, а w₁и w₂— цены двух факторов производства. Тогда задача нахождения максимума прибыли, стоящая перед фирмой, может быть записана в виде

max pf(x₁, 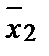)— w₁x₁ — w₂ 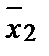. Условие оптимального выбора фактора 1 определить нетрудно. Если 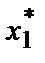— выбор фактора 1, максимизирующий прибыль, то произведение цены выпуска на предельный продукт фактора 1 должно равняться цене фактора 1. В условных обозначениях

pMP₁(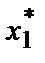, 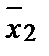) = w₁.

Другими словами, стоимость предельного продукта фактора должна равняться цене фактора. Чтобы понять суть этого правила, представьте, что будет, если фирма примет решение об использовании чуть большего количества фактора 1. Если добавить чуть-чуть этого фактора, x₁, то вы будете производить больше на y = MP₁ x₁, и этот прирост выпуска будет стоить pMP₁ x₁. Но производство этого предельного выпуска обойдется в w₁ x₁. Если стоимость предельного продукта превышает издержки на него, можно увеличить прибыль путем увеличения количества фактора 1. Если стоимость предельного продукта ниже издержек на него, прибыль можно увеличить путем уменьшения объема использования фактора 1. Если прибыль фирмы максимальна, она не должна возрастать при увеличении или уменьшении количества фактора 1. Это означает, что при максимизирующем прибыль выборе факторов и объемов выпуска стоимость предельного продукта pMP₁(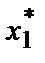, 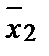)должна равняться цене фактора w₁.

Это условие можно вывести и графически. Используя y для обозначения выпуска фирмы, получаем, что прибыль задается выражением

p = py — w₁x₁ — w₂ .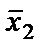

Из этого выражения можно получить y, выразив тем самым выпуск как функцию x₁:

19.

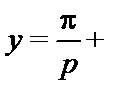
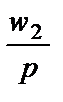
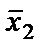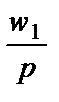+ x₁

Это уравнение описывает изопрофитные линии — все комбинации применяемых факторов производства и выпуска, дающие постоянный уровень прибыли pH. По мере изменения pI мы получаем семейство параллельных прямых линий, наклон каждой из которых равен w₁/pJ, а точка пересечения с вертикальной осью задана выражением (p/p) + (w₂ 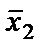/p)K, измеряющим сумму прибыли и постоянных издержек фирмы.

Постоянные издержки постоянны, так что единственная величина, которая действительно изменяется при перемещении с одной изопрофитной линии на другую, есть уровень прибыли. Поэтому более высокие уровни прибыли связываются с теми изопрофитными линиями, точки пересечения которых с вертикальной осью лежат выше.

Тогда задача максимизации прибыли сводится к нахождению точки кривой производственной функции, связываемой с самой высокой изопрофитной линией. Как обычно, она характеризуется условием касания: наклон кривой производственной функции должен равняться наклону изопрофитной линии.

В длительном периоде фирма вольна выбирать уровень использования всех факторов производства. Поэтому задачу максимизации прибыли в длительном периоде можно сформулировать как

max pf(x₁, x₂) — w₁x₁ — w₂x₂.

x₁, x₂N

В основном это та же задача, что и описанная выше для короткого периода, но теперь могут изменяться количества обоих факторов производства.

Условие, описывающее оптимальный выбор, остается по существу тем же, что и раньше, но только теперь мы должны применять его к каждому фактору. Как мы видели ранее, независимо от уровня использования фактора 2 стоимость предельного продукта фактора 1 должна равняться цене этого фактора. Теперь такого же рода условие должно соблюдаться для выбора каждого фактора производства:

pMP₁(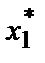, 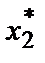) = w₁.

pMP₂(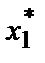, 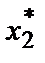) = w₂.

При оптимальном выборе фирмой количества факторов 1 и 2 стоимость предельного продукта каждого фактора должна равняться его цене. В точке оптимального выбора прибыль фирмы не может быть увеличена путем изменения уровня использования какого-либо из факторов.

Доводы в пользу этого те же, что и при обсуждении принятия решений о выпуске, максимизирующем прибыль в коротком периоде. Если бы, например, стоимость предельного продукта фактора 1 превысила цену фактора 1, использование чуть большего количества фактора 1 привело бы к увеличению выпуска на величину MP₁O, которая продавалась бы за pMP₁P долларов. Если стоимость этого выпуска превышает издержки на фактор, используемый для его производства, то расширение использования этого фактора явно окупится.

Эти два условия дают нам два уравнения с двумя неизвестным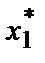и Q и 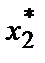R. Если нам известно поведение предельных продуктов как функций x₁ и x₂S, мы сможем выразить оптимальный выбор каждого фактора как функцию цен. Получаемые при этом уравнения известны как уравнения кривых спроса на факторы.

Концепция выявленной максимизации прибыли

Предположим, что есть две комбинации факторов и выпуска, выбранные фирмой при двух разных наборах цен. В момент времени t фирма сталкивается с ценами (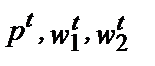 T) и выбирает комбинацию ( 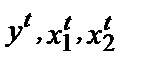U). В момент времени s она сталкивается с ценами ( 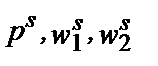V) и выбирает комбинацию ( 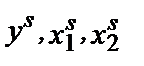W). Если с момента t до момента s производственная функция фирмы не изменилась и фирма максимизирует прибыль, то должно соблюдаться:

— — — —

— — — — .

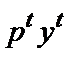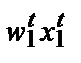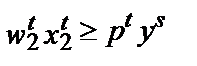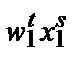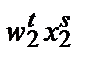
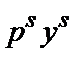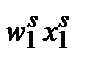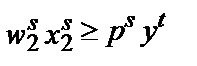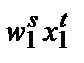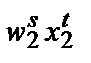Иначе говоря, прибыль, получаемая фирмой при ценах периода t, должна быть больше, чем если бы при этих ценах фирма использовала производственную программу периода s, и наоборот. В случае нарушения любого из этих двух неравенств фирма не могла бы максимизировать прибыль (при условии неизменности технологии).

Соблюдение этих неравенств является буквально аксиомой поведения, максимизирующего прибыль, поэтому его можно назвать слабой аксиомой максимизации прибыли (Weak Axiom of Profit Maximization (WAPM)).

Если сделанный фирмой выбор удовлетворяет WAPM, можно вывести полезное утверждение из области сравнительной статики о том, как ведут себя спрос на факторы и предложение выпуска при изменении цен. Поменяв местами обе стороны неравенства, получим при этом

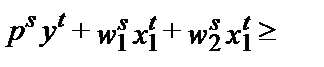
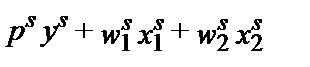(18.4)

а прибавив неравенство (18.4) к неравенству (18.2), получим

(p^t — p^s)y^t — (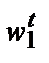 — 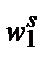) 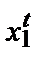— ( — 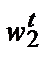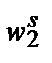) 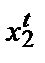³ (p^t — p^s)y^s — ( 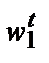— 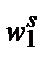) 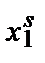— ( — 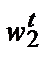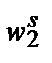) 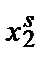. (18.5)

Теперь преобразуем это неравенство:

(p^t — p^s)(y^t — y^s) — (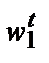 — 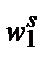)( 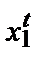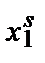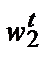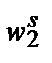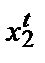— 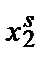) — ( — )( — ) ³ 0. (18.6)

Наконец, определим изменение цен Dp = (p^t — p^s)X, изменение объема выпуска, Dy = (y^t — y^s)Y и т.д., чтобы найти

DpDy — Dw₁Dx₁ — Dw₂Dx₂ ³ 0. (18.7)

Это неравенство — наш конечный результат. Оно свидетельствует, что изменение цены выпуска, умноженное на изменение объема выпуска, минус изменение цены каждого фактора, умноженное на изменение количества этого фактора, должно быть неотрицательной величиной. Это неравенство вытекает исключительно из определения максимизации прибыли. И тем не менее, оно содержит все результаты сравнительной статики в отношении выбора, максимизирующего прибыль!

20. Предложение конкурентной фирмы в коротком и длительном периодах. Квазипостоянные издержки. Излишек производителя в коротком и длительном периоде.

Применим факты, выясненные нами в отношении кривых издержек, для того чтобы вычислить кривую предложения конкурентной фирмы. По определению, конкурентная фирма игнорирует свое влияние на рыночную цену. Таким образом, задачу максимизации, стоящую перед конкурентной фирмой, можно записать:

max py — c(y).

Это говорит просто о том, что конкурентная фирма хочет максимизировать свою прибыль: разность между общим доходом py и издержками c(y).

Какой объем выпуска решит производить конкурентная фирма? Ответ: она будет действовать в точке, где предельный доход равен предельным издержкам, — там, где добавочный доход, приносимый еще одной единицей выпуска, как раз равен добавочным издержкам производства еще одной единицы выпуска. Если бы данное условие не удовлетворялось, фирма всегда могла бы увеличить свою прибыль путем изменения своего объема выпуска.

В случае конкурентной фирмы предельный доход есть просто цена. Чтобы увидеть это, спросим себя, сколько добавочного дохода получит конкурентная фирма, увеличив выпуск на Dy. Мы получим

DR = pDy,

поскольку согласно нашей гипотезе p не изменяется. Поэтому добавочный доход на единицу выпуска задается формулой

DR/Dy = p,

представляющей собой выражение для предельного дохода.

Таким образом, конкурентная фирма выберет объем выпуска y в точке, где предельные издержки как раз равны рыночной цене. В условных обозначениях:

p = MC(y).

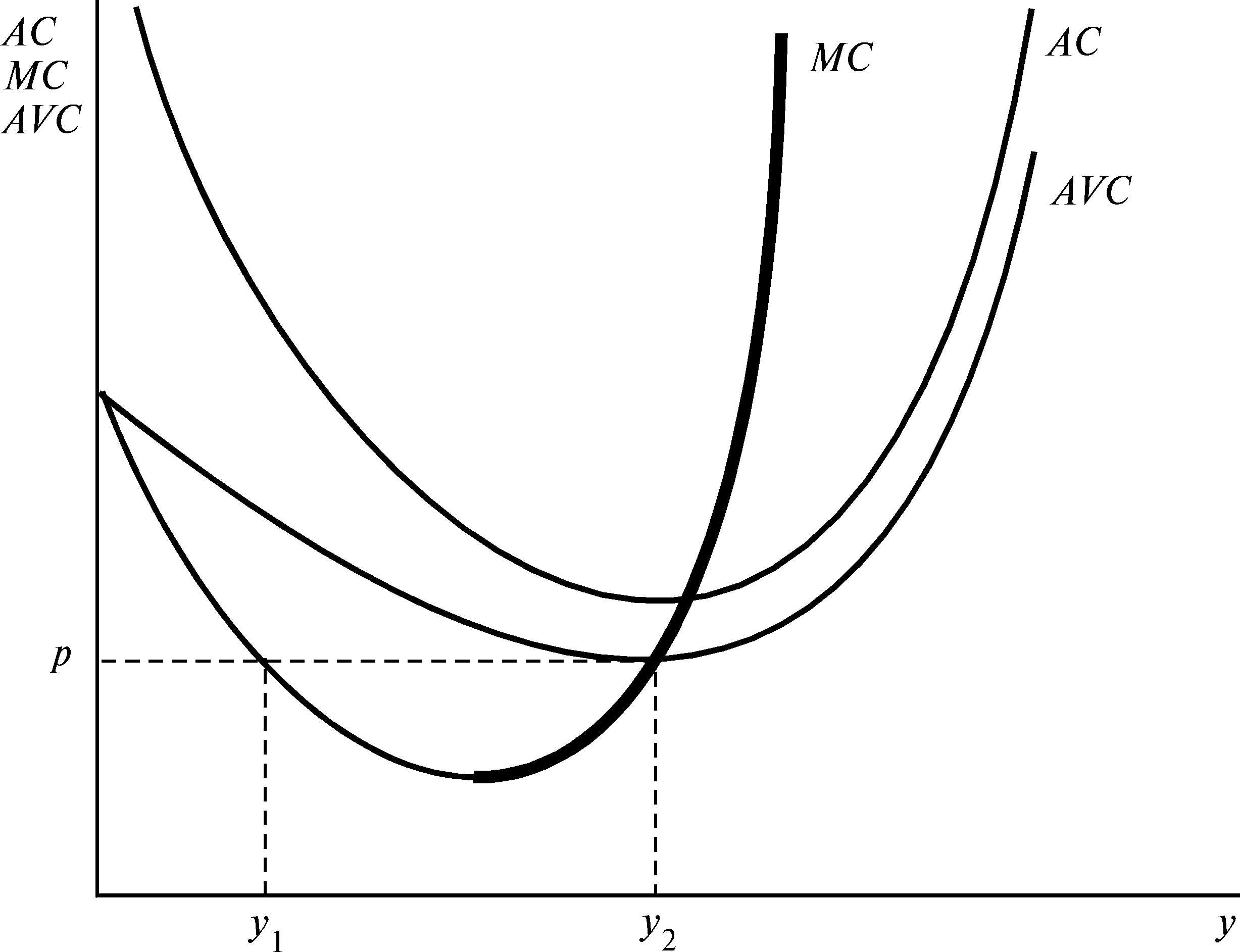Таким образом, при оптимальном объеме выпуска фирма должна производить в точке, где цена равна предельным издержкам. Каков бы ни был уровень рыночной цены p, фирма выберет объем выпуска y, соответствующий условию p = MC(y). Поэтому кривая предельных издержек конкурентной фирмы есть в точности ее кривая предложения. Или, другими словами, рыночная цена есть в точности предельные издержки до тех пор, пока каждая фирма производит объем выпуска, максимизирующий ее прибыль.

В данных рассуждениях предполагается, что выгодно производить что-то. Но в конце концов самым выгодным для фирмы могло бы оказаться и производство нулевого выпуска. Поскольку всегда имеется возможность произвести нулевой объем выпуска, мы должны сравнить точку предполагаемой максимизации прибыли с точкой нулевого производства.

Если фирма производит нулевой выпуск, она по-прежнему должна оплачивать постоянные издержки F. Следовательно, прибыль от производства нуля единиц выпуска равна просто —F. Прибыль от производства объема выпуска y есть py — c_v(y) — F. Фирме выгоднее прекратить деятельность, когда

Поиск по сайту: