 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кривая спроса дуополиста Бертрана
Равновесие в модели Бертрана является устойчивым, если наклон кривой реакции фирмы 1 круче наклона кривой реакции фирмы 2.
В состоянии равновесия в модели Бертрана прибыль отрасли не максимизируется, так как все точки на участке cd контрактной кривой соответствуют более высоким уровням прибыли либо для одной фирмы, либо для обеих.
P2

0 P1
36. Картель. Однопериодовая модель и модель повторяющегося взаимодействия.
Однопериодовая модель
Объединение фирм в целях установления таких цен и объема выпуска, которые максимизировали бы общую прибыль отрасли, известно как картель. Картель— это просто группа фирм, вступающих в сговор, чтобы вести себя как единый монополист и максимизировать сумму своих прибылей.
Таким образом, задача максимизации прибыли для двух фирм состоит в выборе таких объемов выпуска y1 и y2, которые бы максимизировали общую прибыль отрасли:
max p (y 1 + y 2) [ y 1 + y 2] — c 1(y 1) — c 2(y 2).
Условия оптимальности для данной задачи имеют вид
p (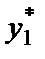 +
+ 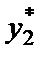 ) +
) +  [
[ 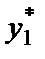 +
+ 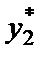 ] = MC 1(
] = MC 1(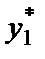 ),
),
p (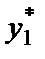 +
+ 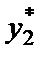 ) +
) +  [
[ 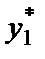 +
+ 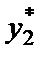 ] = MC 2(
] = MC 2(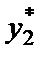 ).
).
Истолкование этих двух условий представляет интерес. Обдумывая, не увеличить ли ей выпуск на D y 1, фирма 1 ожидает двух обычных эффектов: получения добавочной прибыли от продажи большего объема выпуска и сокращения прибыли вследствие снижения цены. Однако рассматривая второй эффект, она теперь учитывает эффект снижения цены как на свой выпуск, так и на выпуск другой фирмы. Это связано с тем, что теперь она заинтересована в максимизации не только своей прибыли, но и общей прибыли отрасли.
Условия оптимальности означают, что предельный доход от добавочной единицы выпуска должен быть одинаковым независимо от того, где он произведен. Отсюда следует, что MC 1(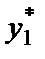 ) = MC 2(
) = MC 2(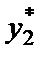 ), так что предельные издержки обеих фирм в равновесии должны быть равны. Если одна из фирм имеет преимущества в издержках, так что ее кривая предельных издержек всегда лежит под кривой предельных издержек другой фирмы, то в равновесии при картеле она всегда будет производить больше выпуска.
), так что предельные издержки обеих фирм в равновесии должны быть равны. Если одна из фирм имеет преимущества в издержках, так что ее кривая предельных издержек всегда лежит под кривой предельных издержек другой фирмы, то в равновесии при картеле она всегда будет производить больше выпуска.
В реальной жизни проблема с решением вступить в картель состоит в том, что всегда есть искушение нарушить условия соглашения. Предположим, например, что две фирмы производят объемы выпуска (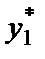 ,
, 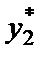 ), максимизирующие прибыль отрасли, и что фирма 1 обдумывает, не произвести ли ей чуть больше выпуска D y 1. Предельная прибыль, которую при этом получит фирма 1, составит
), максимизирующие прибыль отрасли, и что фирма 1 обдумывает, не произвести ли ей чуть больше выпуска D y 1. Предельная прибыль, которую при этом получит фирма 1, составит
37.
 = p (
= p (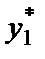 +
+ 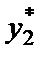 ) +
) + 
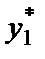 — MC 1(
— MC 1(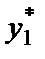 ). (26.5)
). (26.5)
Как мы видели раньше, условие оптимальности для картельного решения есть
p (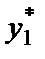 +
+ 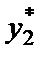 ) +
) + 
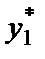 +
+ 
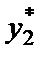 — MC 1(
— MC 1(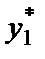 ) = 0.
) = 0.
Преобразование данного уравнения дает
p (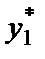 +
+ 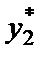 ) +
) + 
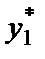 — MC 1(
— MC 1(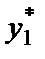 ) = —
) = — 
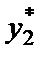 > 0. (26.6)
> 0. (26.6)
Это последнее неравенство возникает потому, что величина Dp/DY отрицательна, так как кривая рыночного спроса имеет отрицательный наклон.
Чтобы убедиться в том, что мы понимаем, как найти решение задачи максимизации прибыли картеля, рассчитаем его для случая нулевых предельных издержек и линейной кривой спроса, которые мы использовали в случае модели Курно.
Функция совокупной прибыли картеля будет иметь вид
p(y 1, y 2) = [ a — b (y 1 + y 2)] (y 1 + y 2) = a (y 1 + y 2) — b (y 1 + y 2)2,
так что условие равенства предельного дохода предельным издержкам будет выражено как
a — 2 b (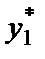 +
+ 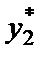 ) = 0,
) = 0,
а это означает, что
 .
.
Поскольку предельные издержки равны нулю, то, как именно разделен выпуск между двумя фирмами, значения не имеет. Единственное, что подлежит определению, это общий объем выпуска отрасли.
Это решение показано на рис.26.5. Здесь мы изобразили изопрофитные кривые для каждой из фирм и выделили геометрическое место точек их касаний друг с другом. Почему данная линия представляет интерес? Поскольку картель пытается максимизировать общую прибыль отрасли, отсюда следует, что предельная прибыль от производства чуть большего объема выпуска любой из фирм должна быть одинаковой, иначе было бы выгодно, чтобы более прибыльная фирма производила больший объем выпуска. Это в свою очередь означает, что наклоны изопрофитных кривых должны быть одинаковы для каждой фирмы; иными словами, изопрофитные кривые должны касаться друг друга. Следовательно, комбинации выпуска, максимизирующие общую прибыль отрасли, т.е. являющиеся решением задачи для картеля, должны лежать на линии, изображенной на рис.26.5.

| Картель. Если прибыль отрасли максимизируется, то предельная прибыль от производства большего объема выпуска для любой фирмы должна быть одинаковой. Это означает, что изопрофитные кривые должны касаться друг друга в точках объемов выпуска, максимизирующих прибыль. |
Модель повторяющегося взаимодействия
В данном случае будет рассматриваться модель кооперирования и наказания в картеле, позволяющая определить условия большей или меньшей устойчивости картельных соглашений.
Предположим, что в отрасли действуют две совершенно одинаковые фирмы, пытающиеся заключить между, собой соглашение об установлении монопольной цены и монопольного объема выпуска, причем каждая из фирм имеет возможность принимать решения в отношении "своих" цены и объема выпуска ежедневно. Зададим себе вопрос: что выгоднее - обмануть другую фирму, т.е. пойти на снижение цены во имя захвата большей доли рынка, или придерживаться соглашения? Чтобы ответить на этот вопрос, надо сопоставить издержки нарушения соглашения (обмана) с выгодами от него.
Выгоды от обмана определяются тем, что, при соблюдении "честной'' фирмой ограничений по объему выпуска с целью поддержания высокой цены, фирме-обманщику выгодно расширять свой выпуск и продажи, получая при этом, в течение заданного периода (длящегося до момента разоблачения) большую прибыль, чем при соблюдении ею соглашения.
Пусть Пс - дневная прибыль, получаемая фирмой при соблюдении соглашения, а По - дневная прибыль в случае его нарушения (т.е. обмана). Тогда По – Пс - дневная выгода от обмана. Ее фирма-обманщик может получать в течение Т дней, до момента разоблачения. Но затем "честная" фирма-участник соглашения предпримет действия, которые снизят будущие прибыли обманщика.
Обозначим через Пн дневную прибыль при несении наказания за обман. Тогда ПС - Пн это дневные издержки обмана для обманщика, или дневные потери прибыли в результате обмана (исчисляемые с (Т+1)-го дня).
Сравнивая выгоды и потери от обмана, необходимо учитывать, что те и другие представляют собой потоки платежей, осуществляемых в разные периоды времени, а следовательно, подлежащие дисконтированию: фирма пойдет на обман только в том случае, если текущая стоимость выгод от обмана окажется для нее больше текущей стоимости потерь от него.
Среди стратегий наказания ''обманщиков'' можно выделить так называемую стратегию курка. Применение в условиях повторяющегося взаимодействия фирм стратегии курка, в частности, ее наиболее "суровой" разновидности (grim-trigger strategy) предполагает следующее. Фирмы-участники сговора согласны ежедневно устанавливать цену РС до тех пор, пока никто не подрывает соглашения. Но в случае обмана наказание состоит в том, Что участники соглашения (включая обманщика) устанавливают цену на уровне предельных издержек. Получившая отражение в названии суровость наказания при данном типе стратегии предопределена тем, что обнаружение обмана служит "спусковым механизмом" бесконечно долгого наказания.
37. Функция ожидаемой полезности фон Нейманна-Моргенштерна и типы отношения к риску. Измерение риска. Методы снижения риска: диверсификация, страхование, приобретение информации.
Функция ожидаемой полезности.
Если предпочтения потребителя в отношении потребления при различных обстоятельствах разумны, то можно использовать для описания этих предпочтений функцию полезности, подобно тому, как это делалось нами в другом контексте. Однако, тот факт, что мы рассматриваем выбор в условиях неопределенности, все же порождает особую структуру задачи выбора.
Мы можем представить функцию полезности зависящей не только от уровней потребления, но и от вероятностей. Предположим, что мы рассматриваем два взаимоисключающих состояния, таких, как дождь и ясная погода, потеря или ее отсутствие, или еще какие-то состояния. Обозначим через  и
и  потребление в состояниях 1 и 2, а через
потребление в состояниях 1 и 2, а через  и
и  - вероятности того, что эти состояния будут иметь место в действительности.
- вероятности того, что эти состояния будут иметь место в действительности.
Если два рассматриваемых состояния взаимоисключающи, так что реально может наступить только одно из них, то  . Но обычно мы выписываем обе вероятности, просто чтобы запись выглядела симметричной.
. Но обычно мы выписываем обе вероятности, просто чтобы запись выглядела симметричной.
С учетом сделанных обозначений, можно записать функцию полезности для потребления в состояниях 1 и 2 в виде  . Это - функция полезности, представляющая предпочтения, имеющиеся у индивида в отношении потребления в каждом из состояний.
. Это - функция полезности, представляющая предпочтения, имеющиеся у индивида в отношении потребления в каждом из состояний.
Ожидаемая полезность
Одной из особенно удобных форм, которую может принимать функция полезности, является следующая:
 .
.
Она говорит нам о том, что функция полезности может быть представлена в виде взвешенной суммы неких функций потребления в каждом состоянии,  и
и  , причем соответствующие веса заданы вероятностями
, причем соответствующие веса заданы вероятностями  и
и  .
.
Если одно из состояний обязательно наступит, так что, скажем,, то  есть полезность определенного потребления в состоянии 1. Аналогичным образом, если
есть полезность определенного потребления в состоянии 1. Аналогичным образом, если  , то
, то  есть функция потребления в состоянии 2. Таким образом, выражение
есть функция потребления в состоянии 2. Таким образом, выражение

представляет собой среднюю полезность, или ожидаемую полезность, структуры потребления ( ).
).
По этой причине, мы называем функцию полезности, имеющую конкретную описанную здесь форму функцией ожидаемой полезности или, иногда, функцией полезности фон Нейманна-Моргенштерна.
Экономисты говорят, что функция ожидаемой полезности "определяется с точностью до монотонного преобразования". Это означает просто, что к ней можно применить линейное преобразование и получить другую функцию ожидаемой полезности. представляющую те же самые предпочтения.
Представление предпочтений в виде ожидаемой полезности удобно, но является ли оно рациональным? Тот факт, что в качестве исходов случайного выбора выступают варианты потребления при различных обстоятельствах, рассматриваемые как различные “потребительские товары”, означает, что, в конечном счете, лишь один из этих исходов будет иметь место в действительности. Либо дом ваш сгорит, либо нет; либо пойдет дождь, либо день будет солнечным. Сам способ постановки нами задачи выбора подразумевает, что реально наступит только один из возможных исходов и, следовательно, фактически будет реализован лишь один из обусловленных планов потребления.
Сказанное имеет, оказывается, очень интересный подтекст. Предположим, что вы размышляете о том, не застраховать ли свой дом от пожара в наступающем году. Производя указанный выбор, вы будете руководствоваться величиной вашего богатства в трех состояниях: его величиной на данный момент (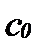 ), его величиной в случае, если ваш дом сгорит (
), его величиной в случае, если ваш дом сгорит ( ), и его величиной в случае, если он не сгорит (
), и его величиной в случае, если он не сгорит ( ).Если
).Если  - вероятность того, что ваш дом сгорит, а
- вероятность того, что ваш дом сгорит, а  - вероятность того. что он не сгорит, то ваши предпочтения в отношении этих трех различных случаев потребления, как правило, могут быть представлены функцией полезности
- вероятность того. что он не сгорит, то ваши предпочтения в отношении этих трех различных случаев потребления, как правило, могут быть представлены функцией полезности  .
.
Предположим, что мы рассматриваем выбор между обладанием богатством сейчас и одним из возможных исходов - скажем, то, сколько денег мы готовы были бы пожертвовать сейчас, чтобы получить чуть больше денег в случае, если дом сгорит. Тогда принимаемое решение должно быть независимым от того, какова будет величина потребления при другом "состоянии природы" - то есть, от того, какова будет величина потребления в случае, если дом не будет уничтожен. Ведь дом либо сгорит. либо - нет. Если случится так, что он сгорит, то величина дополнительного богатства не должна зависеть от той величины богатства, которой вы располагали бы, если бы дом не сгорел. Прошлое есть прошлое - поэтому то, что не произошло, не должно влиять на величину потребления при исходе, имеющем место в действительности.
Обратите внимание на то, что сказанное есть предпосылка в отношении предпочтений индивида. Она может нарушаться. Когда люди решают, какую из двух вещей выбрать, количество третьей имеющейся у них вещи обычно тоже имеет значение. Выбор между кофе и чаем вполне может зависеть от того, сколько у вас имеется сливок. Но это происходит потому, что вы пьете кофе со сливками. Если бы вы рассматривали ситуацию, в которой вы бросаете игральную кость и, в зависимости от исхода, получаете либо кофе, либо чай, либо сливки, то количество сливок, которое вы могли бы при этом получить, не должно было бы повлиять на ваши предпочтения в отношении кофе и чая. Почему? Потому что вы получаете либо одно, либо другое: если, в конечном счете, вам достаются сливки, то тот факт, что вы могли бы получить либо кофе, либо чай, значения не имеет.
Таким образом, при выборе в условиях неопределенности естественного рода "независимость" потребления при различных исходах существует потому, что соответствующие варианты потребления реализуются раздельно - при разных "состояниях природы". Выбор, планируемый людьми при одном "состоянии природы", должен быть независим от вариантов выбора, планируемых ими для других "состояний природы". Эта предпосылка известна как предпосылка о независимости. Из нее вытекает очень специфическая структура функции полезности для обусловленного потребления: аддитивность по различным наборам обусловленного потребления.
Иными словами, если  ,
,  и
и  представляют собой потребление при различных исходах, а
представляют собой потребление при различных исходах, а  ,
,  и
и  - это вероятности наступления указанных трех различных исходов, то, при соблюдении предпосылки о независимости, на которую мы ссылались выше, функция полезности должна принять вид
- это вероятности наступления указанных трех различных исходов, то, при соблюдении предпосылки о независимости, на которую мы ссылались выше, функция полезности должна принять вид
 .
.
Это - функция, которую мы назвали функцией ожидаемой полезности. Заметьте себе, что функция ожидаемой полезности, и в самом деле, удовлетворяет тому свойству, что предельная норма замещения одного из двух товаров на другой не зависит от того, сколько у нас имеется третьего товара. Предельная норма замещения, скажем, товара 2 товаром 1 принимает вид
 =
=
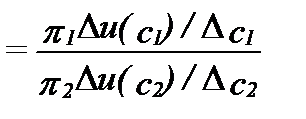 .
.
Эта MRS зависит только от имеющегося количества товаров 1 и 2, а не зависит от имеющегося количества товара 3.
Особенности поведения расположенных к риску, нерасположенных к риску и нейтральных к риску экономических субъектов.
Нерасположенность к риску
Применим анализ с позиций ожидаемой полезности к решению простой задачи выбора. Допустим, что в данный момент у потребителя имеется богатства на 10 долл. и что он размышляет, стоит ли сыграть в игру, которая с вероятностью в 50 процентов принесет ему выигрыш в 5 долл. и с вероятностью в 50 процентов - проигрыш в 5 долл. Богатство его, следовательно, становится случайной величиной: имеется вероятность в 50 процентов, что он останется с 5 долларами, и вероятность в 50 процентов, что у него, в итоге, будет 15 долларов. Ожидаемое значение его богатства равно 10 долл., а ожидаемая полезность есть
 .
.
Это изображено на рис.12.2. Ожидаемая полезность богатства есть средняя двух чисел u(15$) и u(5$), обозначенных на графике 0,5u(5) и 0,5u(15). Мы изобразили также полезность ожидаемого значения богатства, которую обозначили u(10$). Обратите внимание на то, что на данном графике ожидаемая полезность богатства меньше полезности ожидаемого значения богатства. То есть:.
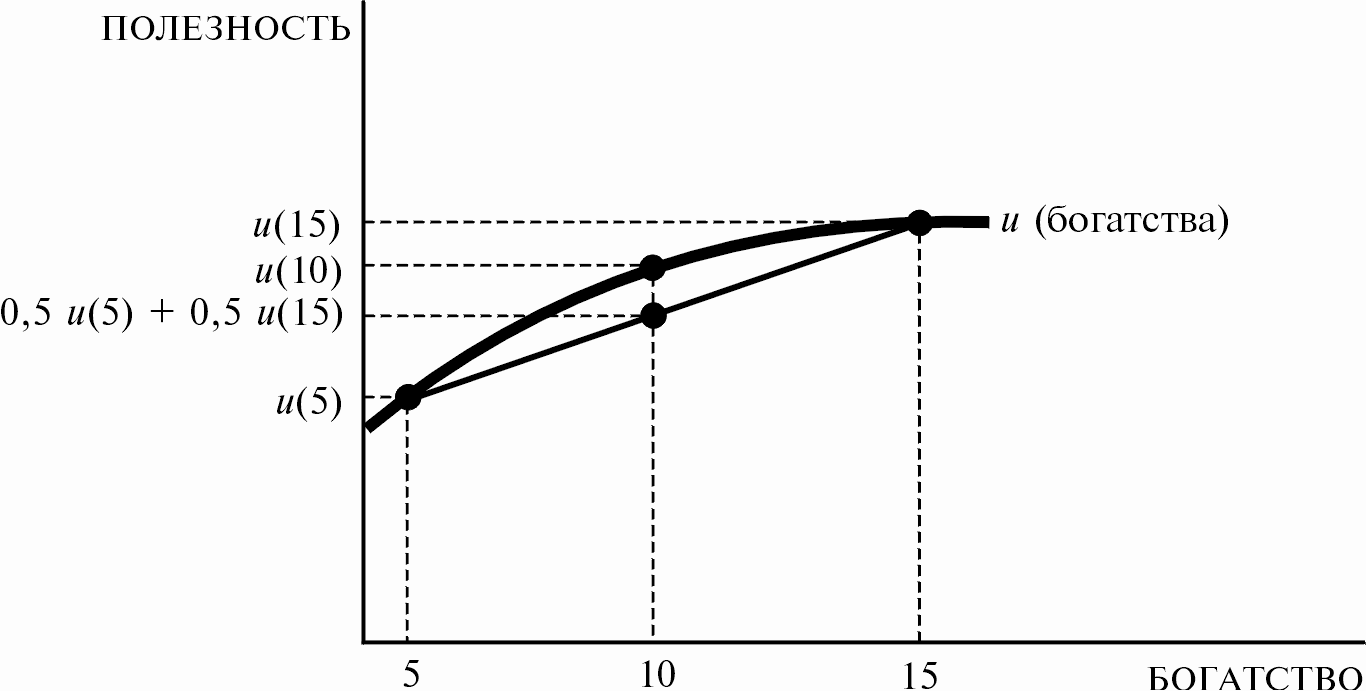
Рис.12.2 Нерасположенность к риску.
В этом случае мы говорим, что потребитель не расположен к риску, поскольку предпочитает иметь ожидаемое значение своего богатства, нежели вступить в игру. Конечно, предпочтения потребителя могли бы оказаться такими, что он предпочел бы случайное распределение богатства его ожидаемому значению, и в таком случае мы говорим, что потребитель расположен к риску. Пример такого рода приведен на рис.12.3.
Обратите внимание на различие между рис. 12.2 и 12.3. Потребитель, не расположенный к риску, имеет вогнутую функцию полезности - ее наклон, по мере возрастания богатства, уменьшается.
Расположенность к риску
У потребителя, расположенного к риску, функция полезности выпуклая - ее наклон, по мере возрастания богатства, становится больше. Следовательно, кривизна функции полезности измеряет отношение потребителя к риску. Как правило, чем более вогнутой является функция полезности, тем в большей степени потребитель не расположен к риску, а чем более она выпукла, тем в большей степени потребитель расположен к риску.
Нейтральность к риску
Промежуточным является случай линейной функции полезности. Здесь потребитель нейтрален к риску: ожидаемая полезность богатства есть полезность его ожидаемого значения. В этом случае потребителя совершенно не заботит степень рискованности получения его богатства - его интересует лишь ожидаемое значение последнего.
Измерение риска. Плата за риск.
Величина риска, характеризующая данный актив, зависит от его корреляции с другими активами.
Риск по данному активу удобно измерять по отношению к риску по фондовому рынку в целом. Мы называем степень риска акции, измеренную относительно риска по фондовому рынку в целом, бетой акции и обозначаем ее греческой буквой A. Таким образом, если i обозначает акции какой-то конкретной компании, то степень риска этих акций по отношению к фондовому рынку в целом мы обозначим
B. Грубо говоря:
 .
.
Если бета данного вида акций равна 1, степень риска по ним - такая же, как и по фондовому рынку в целом; при росте курсов акций на фондовом рынке в среднем на 10 процентов курс акций данного вида вырастет, в среднем, на 10 процентов. Если бета акций данного вида составляет менее 1, то при росте курсов акций на фондовом рынке в среднем на 10 процентов курс акций данного вида вырастет менее, чем на 10 процентов. Оценку беты акций позволяют получить статистические методы, определяющие степень чувствительности движений одной переменной по отношению к движениям другой, и существует много консультационных инвестиционных служб, способных предоставить вам оценки беты конкретных видов акций.
Сформулируем принцип равновесия на рынке рисковых активов: все активы, с учетом поправки на риск, должны приносить одну и ту же норму дохода.
Загвоздка - в поправке на риск. Как это сделать? Ответ дан проведенным ранее анализом оптимального выбора. Вспомним, что мы рассматривали выбор оптимального портфеля, содержащего один безрисковый и один рисковый актив. Рисковый актив интерпретировался нами как взаимный фонд - диверсифицированный портфель, включающий в себя много рисковых активов. В настоящем параграфе мы предположим, что этот портфель состоит только из рисковых активов.
Тогда можно отождествить ожидаемый доход на этот рыночный портфель рисковых активов с ожидаемым рыночным доходом, , а стандартное отклонение рыночного дохода с рыночным риском,
. Доход на надежный актив обозначим как
, доход, "свободный" от риска.
Цена риска, p, задана формулой: .
Выше было сказано, что величина риска, характеризующая данный актив i, взятая по отношению к общему рыночному риску, обозначается как . Это означает, что для измерения общей величины риска, характеризующей актив i, следует умножить
на рыночный риск,
. Следовательно, общая величина риска по данному активу задается
.
Каковы издержки несения этого риска? Просто умножьте общую величину риска, , на цену риска. Это и даст нам поправку на риск:
поправка на риск =
=
= .
Методы снижения риска: диверсификация, страхование, приобретение информации.
Диверсификация
Обратимся теперь к другой теме, связанной с неопределенностью, - выгодам от диверсификации. Предположим, что вы раздумываете, стоит ли вложить 100 долл. в две различные компании, одна из которых производит очки от солнца, а другая - плащи. Согласно долгосрочному прогнозу погоды, следующее лето в равной степени может оказаться и дождливым, и солнечным. Каким образом вам лучше инвестировать ваши деньги?
Не разумнее ли было бы застраховаться от случайностей и вложить некоторую сумму денег в каждую из указанных компаний? Путем диверсификации своих акционерных вложений в обе компании, вы можете получить на них доход более надежный, а потому - более желательный, если вы - человек, не расположенный к риску.
Допустим, например, что акции компании по производству плащей и акции компании по производству очков от солнца в настоящее время стоят 10 долл. штука. Если лето окажется дождливым, то акции компании по производству плащей будут стоить 20 долл. штука, а акции компании по производству очков от солнца - 5 долл. Если же лето выдастся солнечное, результаты будут обратными: акции компании, производящей очки от солнца, будут стоить по 20 долл., а акции компании, производящей плащи, - по 5 долл. Вложив все 100 долл. в компанию по производству очков от солнца, вы делаете ставку в игре, которая с вероятностью 50 процентов принесет вам 200 долл. и с вероятностью 50 процентов - 50 долл. Такой же величины вознаграждение вы получите, если вложите все деньги в компанию по производству плащей: в обоих случаях ваш ожидаемый выигрыш составляет 125 долл.
Посмотрите, однако, что получится, если вы вложите половину денег в каждую из компаний. Тогда, если лето будет солнечным, вы получите 100 долл. от вложений в компанию по производству очков от солнца и 25 долл. от вложений в компанию по производству плащей. Если же лето окажется дождливым, вы получите 100 долл. от вложений в компанию по производству плащей и 25 долл. от вложений в компанию по производству очков от солнца. В любом случае, вы гарантированно получаете 125 долл. Путем диверсификации инвестиций в обе компании вам удалось снизить совокупный риск своих вложений, в то же время сохраняя неизменным ожидаемый выигрыш.
В этом примере осуществить диверсификацию было совсем легко: между обоими активами имелась совершенно отрицательная корреляция - когда стоимость одного из них увеличивалась, стоимость другого уменьшалась. Пары активов, подобные этой, могут быть исключительно ценными, так как с их помощью можно очень сильно снижать риск. Однако, увы, их также бывает очень трудно найти. Курсовые стоимости большинства активов движутся в одном и том же направлении: когда растет курс акций "General Motors Company", растет и курс акций компании "Ford". Но поскольку движение цен активов не характеризуется совершенной положительной корреляцией, могут возникать некоторые выгоды от диверсификации.
Страхование
Кое-что о страховании уже было сказано в ответе на вопрос о склонности индивида к риску. Так же показательным является спрос на страхование. Применим функцию ожидаемой полезности к спросу на страхование, рассматривавшемуся нами ранее. Вспомним, что в примере, о котором идет речь, индивид имел богатство стоимостью 35 000 долл. и мог понести убытки в размере 10 000 долл. Вероятность убытков составляла 1 процент, и покупка страхового полиса на сумму K долларов обходилась ему в rK долларов. Исследуя эту задачу выбора с помощью кривых безразличия, мы увидели, что оптимальный выбор суммы страхования определяется условием равенства MRS потребления при одном исходе потреблением при другом исходе - в случае убытков или в случае отсутствия убытков - отношению  . Обозначим через
. Обозначим через  вероятность того, что убытки будут иметь место, и через (
вероятность того, что убытки будут иметь место, и через ( ) вероятность того, что ее не будет.
) вероятность того, что ее не будет.

Рис.12.3 Потребитель, расположенный к риску. Для потребителя, расположенного к риску, ожидаемая полезность богатства, 0,5u(5)+0,5u(15), больше полезности ожидаемого значения богатства, u(10).
Пусть состояние 1 - это ситуация. в которой убытков нет, так что богатство потребителя в этом состоянии есть
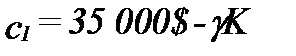 ,
,
и пусть состояние 2 - это ситуация несения убытков, которой соответствует богатство
 .
.
Тогда оптимальный выбор суммы страхования потребителем определяется условием равенства MRS его потребления при одном исходе потреблением при другом исходе отношению цен:
 (12.1) (12.1)
|
Теперь посмотрим на страховой контракт с точки зрения страховой компании. С вероятностью  ей придется выплатить K и с вероятностью
ей придется выплатить K и с вероятностью  - ничего. Независимо от исхода, она получит премию
- ничего. Независимо от исхода, она получит премию 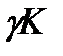 . Тогда ожидаемая прибыль страховой компании, P, есть
. Тогда ожидаемая прибыль страховой компании, P, есть
 .
.
Предположим, что в среднем контракт является для страховой компании безубыточным. Иными словами, она предлагает страхование по "справедливой" ставке страховой премии, где " справедливая" означает то, что ожидаемое значение суммы страхования как раз равно издержкам на него. Тогда мы получаем
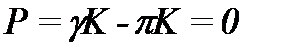 ,
,
что подразумевает  .
.
Подставив это выражение в уравнение (12.1), получаем
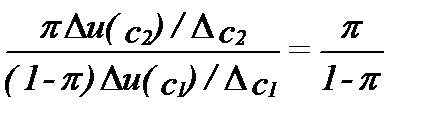 .
.
Взаимно уничтожив  , получаем, что оптимальная сумма страховки должна удовлетворять условию
, получаем, что оптимальная сумма страховки должна удовлетворять условию
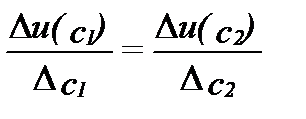 (12.2) (12.2)
|
В этом уравнении говорится, что предельная полезность дополнительного доллара дохода в случае потери должна равняться предельной полезности дополнительного доллара дохода в случае отсутствия потери.
Предположим, что потребитель не расположен к риску, так что по мере увеличения имеющейся у него суммы денег предельная полезность денег для него снижается. Тогда, если  , предельная полезность при
, предельная полезность при  будет меньше, чем предельная полезность при
будет меньше, чем предельная полезность при 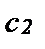 , и наоборот. Более того, если предельные полезности дохода при
, и наоборот. Более того, если предельные полезности дохода при  и
и  равны, как в уравнении (12.2), то должно соблюдаться
равны, как в уравнении (12.2), то должно соблюдаться  . Применив формулы для
. Применив формулы для  и
и  , мы находим:
, мы находим:
 ,
,
что подразумевает K=10 000$. Это означает, что, имея шанс заплатить за страховой полис "справедливую" премию, потребитель, не расположенный к риску, всегда предпочтет застраховаться полностью.
Это происходит потому, что полезность богатства в каждом состоянии зависит только от общей величины богатства, имеющейся у потребителя в этом состоянии, - а не от того, что он мог бы иметь в каком-то другом состоянии - так что, если общие величины богатства, имеющиеся у потребителя в каждом состоянии, равны, то предельные полезности богатства также должны быть равны.
Подытожим сказанное: если потребителю, который не расположен к риску и максимизирует ожидаемую полезность, предлагается сделка справедливого страхования от убытков, он предпочтет в оптимуме застраховаться полностью.
38. Карты кривых безразличия и норма замещения при выборе потребителя в мире двух обусловленных благ. Бюджетная линия и особенности оптимума индивидов с разным отношением к риску в мире двух обусловленных благ.

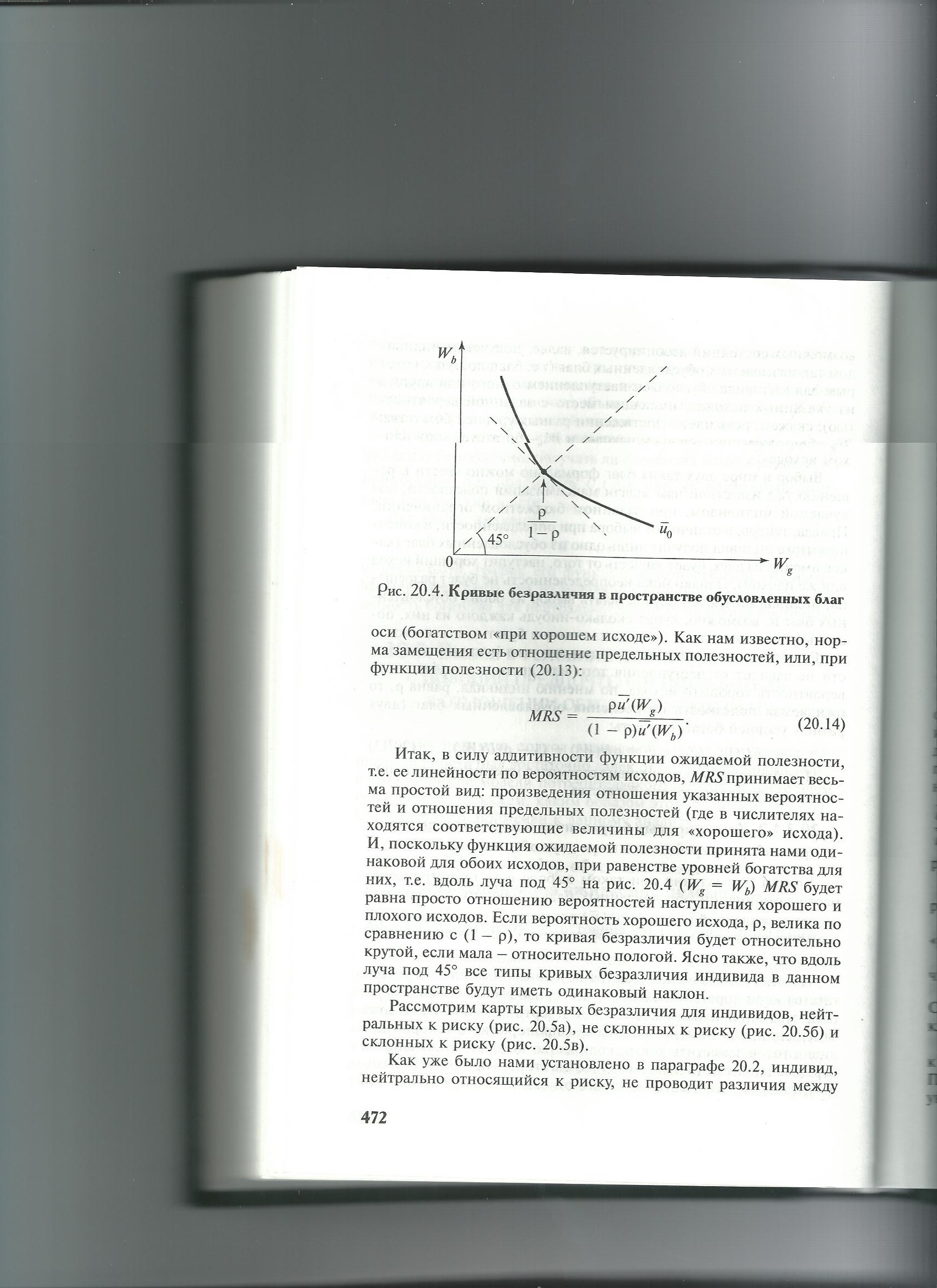




39. Максимизация прибыли и производный спрос на факторы производства: формальный и графический анализ. Эффект замещения, эффект выпуска и общий эффект изменения цены фактора производства.



40. Выведение кривой индивидуального предложения труда. Модель распределения времени между досугом и работой. Рыночное предложение труда.
Предпосылка: труд НЕ является экономическим благом, обладающим свойством редкости и желанности. Для производителей (фирм-нанимателей) труд обладает двумя этими свойствами, но для потребителей нет. Для них труд обладает свойством редкости, но в отношении желанности – не утверждать слишком смело. Гораздо проще «обойти» проблему желанности труда для индвидов, попытавшись ответить на следующие вопросы: почему люди вообще работают, причем одни – больше, а другие – меньше, и почему они могут по-разному реагировать на изменения в зарплате? Ответ интуитивно ясен. Мы работает ради заработка, позволяющего купить экономические блага. Но из этого не следует, что труд для нас экономическое благо. Труд – это механизм превращения отказа от досуга в получение других экономических благ, олицетворяемым композитным товаром, приобретаемым на доход. Редкость досуга при этом специфична, что связано с ее особым, природным характером. Фонд времени, подлежащий обмену между досугом и композитным товаром, не только не может превысить 24 часа, но и обязательно будет меньше, скажем, 18 часов, т.к. в него не включается время сна. L (подчеркивание вверху)– этот фонд времени, не подлежащий изменению начальный запас, или фонд первоначальной наделенности. Le – количество досуга, L – труда. Тогда предлагаемое индивидом количество труда находится по остаточному принципу, как разность (L-Le*), где Le* - количество досуга, выбираемое индивидом.
Специфичность бюджетного ограничения.
Пусть индивид имеет только заработанный им, при номинальной (почасовой) ставке з-п w, доход, который он целиком тратит на товар Y с ценой Py. Тогда: Py*Y=w(L-Le). Почасовая з-п w есть цена товара «досуг». Наклон данного бюджетного ограничения, взятый по абс.величине, есть почасовая з-п w: если индивид предпочитает предаваться досугу в течение всех L часов, то ничего не заработает и не сможет купить товара Y; проработав один час, он получит з-п в размере w и сможет купить w/Pу единиц товара У. Т.е. реальная з-п w есть альтернативная стоимость одного часа досуга. При изменении наклона бюджетная линия будет поворачиваться вокруг точки своего пересечения с горизонтальной осью, т.е. точки начального запаса L (макс.возможное потребление досуга равно L и не зависит от его цены), в то время как координата ее пересечения осью (w* L)/Py будет меняться.
Будем считать, что предпочтения индивида в отношении досуга и композитного товара стандартны, т.е. удовлетворяют всем аксиомам потреб.выбора, и они описываются функцией полезности U(Le,Y). Определение выбираемого количества досуга сводится к решению задачи нахождения внутреннего оптимума потребителя. Найдя набор (Le*,Y*), который при заданных L, w и Ру, будет решением задачи: max U(Le,Y) при Py*Y+w*Le=w* L, отсюда величина предложения труда L*= L - Le*

Модель индивидуального предложения труда.
Индивид может выбрать одну из двух альтернатив: либо очень много работать и иметь сравнительно высокий уровень потребления, либо работать мало и иметь низкий уровень потребления. Величина потребления и затрат труда определяется взаимодействием предпочтений потребителя и его бюджетного ограничения. Предположим, что первоначально у потребителя имеется некоторый денежный доход M, получаемый им независимо от того, работает он или нет. Это может быть, например, доход от инвестиций или же доход, выплачиваемый родственниками. Назовем эту сумму нетрудовым доходом потребителя. (Потребитель мог бы иметь нетрудовой доход, равный нулю, но мы допускаем, что он положителен.)
Обозначим величину потребления данного потребителя через C, а цену потребления через p. Тогда, если ставку заработной платы обозначить w, а предлагаемое им количество труда — L, то получим следующее бюджетное ограничение:
pC = M + wL.
Оно показывает, что стоимость того, что потребляет потребитель, должна равняться сумме его нетрудового и трудового доходов.
Попробуем сравнить приведенную выше формулу с приведенными ранее примерами бюджетных ограничений. Главное отличие состоит в том, что в данной формуле в правой части уравнения оказалось нечто, что потребитель выбирает — предложение труда. Мы легко можем перенести его в левую часть уравнения, получив при этом
pC — wL = M.
Это уже лучше, но у нас стоит знак "минус" там, где обычно стоит знак "плюс". Можем ли мы это исправить? Предположим, что существует некая максимально возможная величина предложения труда — 24 часа в сутки, 7 дней в неделю или что-то другое, что совместимо с используемыми нами единицами измерения. Обозначим это количество рабочего времени через  . Тогда, прибавив w
. Тогда, прибавив w  к каждой части уравнения и преобразовав его, получаем
к каждой части уравнения и преобразовав его, получаем
pC + w( -L) = M+w
-L) = M+w 
pC + w(— L) = M + w.CD
Введем определение  = M/p — величины потребления данного потребителя в случае, если он не работает вовсе. Иными словами,
= M/p — величины потребления данного потребителя в случае, если он не работает вовсе. Иными словами,  — это его начальный потребительский запас, поэтому можно записать
— это его начальный потребительский запас, поэтому можно записать
pC + w( — L) = p
— L) = p  + w
+ w 
Теперь имеем уравнение, очень похожее на те, которые мы встречали раньше. У нас есть две переменные, характеризующие выбор потребителя, в левой части и две переменные, характеризующие начальный запас, в правой части. Переменную  — L можно трактовать как величину "досуга", т.е. как время, не являющееся рабочим временем. Обозначим "досуг" с помощью переменной R (от слова "релаксация!"), так что R =
— L можно трактовать как величину "досуга", т.е. как время, не являющееся рабочим временем. Обозначим "досуг" с помощью переменной R (от слова "релаксация!"), так что R =  — L. Тогда общая величина имеющегося времени досуга есть
— L. Тогда общая величина имеющегося времени досуга есть  =
=  , и бюджетное ограничение принимает вид
, и бюджетное ограничение принимает вид
pC + wR = p  + w
+ w 
Приведенное выше уравнение формально идентично самому первому уравнению бюджетного ограничения, записанному нами в настоящей главе. Однако ему можно дать гораздо более интересное истолкование. Оно говорит о том, что сумма стоимостей потребления потребителя и его досуга должна быть равна сумме стоимостей его начального потребительского запаса и его начального временного запаса, причем его временной запас оценивается по ставке заработной платы. Ставка заработной платы оказывается не только ценой труда, но и ценой досуга.
Экономисты говорят иногда, что ставка заработной платы есть альтернативная стоимость досуга. Правую часть этого бюджетного ограничения иногда называют полным доходом потребителя, или его предполагаемым доходом. Он показывает стоимость того, чем владеет потребитель — его начального потребительского запаса, если таковой имеется, и начального запаса его собственного времени. Данный доход следует отличать от измеряемого дохода потребителя, являющегося просто доходом, получаемым потребителем от продажи части своего времени.
Хорошо то, что данное бюджетное ограничение — совершенно такое же, как и бюджетные ограничения, виденные нами ранее. Оно проходит через точку начального запаса 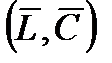 и имеет наклон, равный —w/p. Начальный запас — это то, что получил бы потребитель, если бы совсем не участвовал в рыночных сделках, а наклон бюджетной линии говорит нам о пропорции, в которой один товар может быть обменен на другой на рынке.
и имеет наклон, равный —w/p. Начальный запас — это то, что получил бы потребитель, если бы совсем не участвовал в рыночных сделках, а наклон бюджетной линии говорит нам о пропорции, в которой один товар может быть обменен на другой на рынке.

A Кривые безразличия B Кривая предложения труда

Рисунок 9.8 Индивидуальное предложение труда.
Оптимальный выбор, как показано на рис.9.8, имеет место тогда, когда предельная норма замещения — пропорция обмена между потреблением и досугом — равна w/p, реальной заработной плате. Cтоимость, в которую обойдется потребителю дополнительное потребление, получаемое благодаря чуть бóльшим затратам труда, должна быть как раз равна стоимости потерянного досуга, которым пришлось пожертвовать, чтобы создать это дополнительное потребление. Реальная заработная плата есть величина потребления, которую может приобрести потребитель, отказавшись от одного часа досуга.
Поиск по сайту: