 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ценообразование по схеме двойного тарифа
Суть данной схемы ценообразования состоит в следующем: с потребителей взимается, во-первых, фиксированная ''входная'' плата за доступ к потреблению данного товара, а во-вторых, плата (одинаковая) за каждую потребленную единицу товара.
Имеется множество других применений двойных тарифов: Polaroid продает фотоаппарат по одной цене, а пленку — по другой. Принимая решение о том, покупать фотоаппарат или нет, люди, предположительно, учитывают и стоимость пленки. Компания, производящая лезвия для бритья, продает бритву по одной цене, лезвия — по другой — и снова цена, устанавливаемая ею на лезвия, влияет на спрос на бритвы, и наоборот.
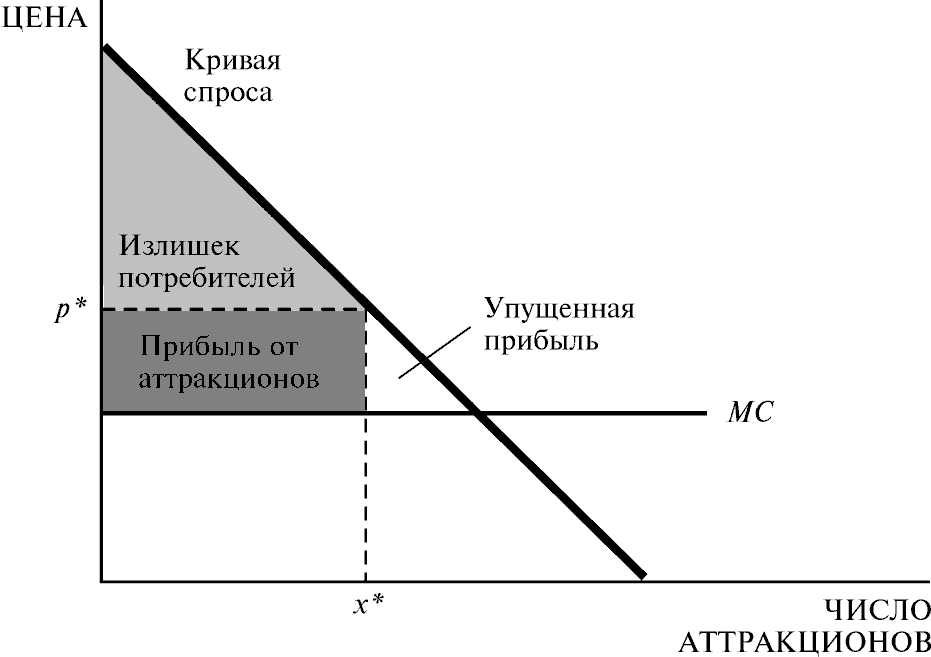
| Дилемма Диснейленда. Если владельцы парка установят цену p*, то спрос на аттракционы составит x*. Излишек потребителей измеряет цену, которую владельцы могут установить за вход в парк. Общая прибыль фирмы максимизируется, когда владельцы устанавливают цену, равную предельным издержкам. | Рис. 24.5 |
Нетрудно увидеть, что общая прибыль максимизируется при цене, равной предельным издержкам: как мы видели ранее, эта цена дает максимально возможный излишек потребителя плюс излишек производителя. Поскольку монополист получает возможность затребовать у людей их излишек потребителей, установление цены, равной предельным издержкам, и платы за вход, приводящей к извлечению излишка потребителей, есть политика максимизации прибыли.
И действительно, именно этой политики придерживаются Диснейленд и большинство других парков аттракционов. Существует единая плата за вход, но зато аттракционы внутри парка бесплатные. Похоже, что предельные издержки на аттракционы меньше, чем транзакционные издержки сбора отдельной платы за них.
Алгебраически данную модель можно формализовать следующим образом:
Прибыль (П) при данной схеме ценообразования есть сумма прибыли от входной платы Пе и прибыли от продаж Пs.
Запишем условие максимизации прибыли:
Max П = Пе+(p — AC)(x1+x2)
То есть если на рынке действует две группы покупателей с линейными кривыми спроса вида x1 = a — bp1 и x2 = c — dp2, то выражение примет следующий вид:
Max П = CS1(p)+CS2(p)+(p — AC)(x1+x2),
Где CS1(p1) и CS2(p2) – потребительские излишки соответственно первой и второй групп покупателей, выраженные как функция от цены, а x1+x2 – функция совокупного спроса.
Решив уравнение максимизации (частная производная прибыли по цене), мы найдем цену и размер потребительских излишков, больший из которых и будет равен Пе.
33. Дуополия Курно. Равновесие Нэша. Модель Курно для n фирм.
Основной предпосылкой модели Курно является то, что фирма - олигополист стремится максимизировать свою прибыль, считая выпуск соперника заданным. При этом предельные издержки олигополистов являются постоянными величинами. Начнем с предположения о том, что согласно ожиданиям фирмы 1 фирма 2 произведет 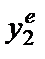 единиц выпуска. (Буква e обозначает ожидаемый выпуск). Если фирма 1 решит произвести y1 единиц выпуска, то согласно ее ожиданиям общий произведенный объем выпуска составит Y = y 1 +
единиц выпуска. (Буква e обозначает ожидаемый выпуск). Если фирма 1 решит произвести y1 единиц выпуска, то согласно ее ожиданиям общий произведенный объем выпуска составит Y = y 1 + 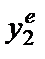 и будет продан по рыночной цене p (Y) = p (y 1 +
и будет продан по рыночной цене p (Y) = p (y 1 + 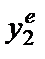 ). Задача максимизации прибыли для фирмы 1 тогда принимает вид
). Задача максимизации прибыли для фирмы 1 тогда принимает вид
max p (y 1 + 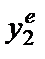 ) y 1 — c (y 1)
) y 1 — c (y 1)
При любом данном мнении относительно объема выпуска 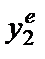 фирмы 2, для фирмы 1 будет существовать некий оптимальный выбор объема выпуска y1. Запишем эту функциональную взаимосвязь между ожидаемым выпуском фирмы 2 и оптимальным выпуском фирмы 1 как y 1 = f 2(
фирмы 2, для фирмы 1 будет существовать некий оптимальный выбор объема выпуска y1. Запишем эту функциональную взаимосвязь между ожидаемым выпуском фирмы 2 и оптимальным выпуском фирмы 1 как y 1 = f 2(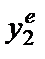 ). Данная функция есть просто функция реакции В нашей первоначальной трактовке функция реакции показывала выпуск ведомого как функцию от выбора объема выпуска лидером. В рассматриваемом случае функция реакции показывает оптимальный выбор одной фирмы как функцию ее ожиданий в отношении выбора другой фирмы. Хотя интерпретация функции реакции в двух этих случаях и различна, ее математическое определение совершенно одинаково. Подобным же образом можно вывести кривую реакции фирмы 2:
). Данная функция есть просто функция реакции В нашей первоначальной трактовке функция реакции показывала выпуск ведомого как функцию от выбора объема выпуска лидером. В рассматриваемом случае функция реакции показывает оптимальный выбор одной фирмы как функцию ее ожиданий в отношении выбора другой фирмы. Хотя интерпретация функции реакции в двух этих случаях и различна, ее математическое определение совершенно одинаково. Подобным же образом можно вывести кривую реакции фирмы 2:
y 2 = f 2(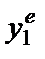 ), показывающую оптимальный выбор объема выпуска фирмы 2 при данных ожиданиях в отношении объема выпуска
), показывающую оптимальный выбор объема выпуска фирмы 2 при данных ожиданиях в отношении объема выпуска 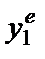 фирмы 1. Вспомним теперь, что каждая из фирм выбирает свой объем выпуска, предполагая, что выпуск другой фирмы будет равен соответственно
фирмы 1. Вспомним теперь, что каждая из фирм выбирает свой объем выпуска, предполагая, что выпуск другой фирмы будет равен соответственно 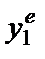 или
или 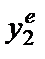 . Для произвольных значений
. Для произвольных значений 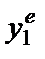 и
и 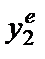 это произойти не может вообще говоря, оптимальный объем выпуска y1 фирмы 1, будет отличаться от ожидаемого фирмой 2 объема выпуска
это произойти не может вообще говоря, оптимальный объем выпуска y1 фирмы 1, будет отличаться от ожидаемого фирмой 2 объема выпуска 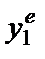 фирмы 1. Поищем такую комбинацию объемов выпуска (
фирмы 1. Поищем такую комбинацию объемов выпуска (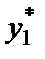 ,
, 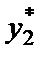 ), чтобы при предположении о том, что фирма 2 производит
), чтобы при предположении о том, что фирма 2 производит 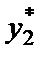 , оптимальный объем выпуска для фирмы 1 составил
, оптимальный объем выпуска для фирмы 1 составил 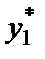 , а оптимальный объем выпуска для фирмы 2 при предположении, что фирма 1 по-прежнему производит
, а оптимальный объем выпуска для фирмы 2 при предположении, что фирма 1 по-прежнему производит 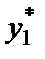 , составил
, составил 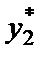 . Другими словами, выбор объемов выпуска (
. Другими словами, выбор объемов выпуска (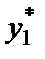 ,
, 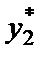 ) удовлетворяет уравнениям
) удовлетворяет уравнениям
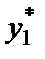 = f 1(
= f 1(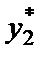 )
)
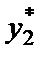 = f 2(
= f 2(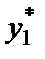 ).
).
Такая комбинация объемов выпуска известна как равновесие по Курно. В равновесии по Курно каждая из фирм максимизирует свою прибыль при данных ожиданиях относительно выбора объема выпуска другой фирмой, и, более того, эти ожидания в равновесии сбываются: каждая фирма в оптимуме решает производить именно тот объем выпуска, производства которого ожидает от нее другая фирма. В равновесии по Курно ни одна из фирм не сочтет для себя выгодным изменить объем выпуска, как только обнаружит, каков выбор, фактически сделанный другой фирмой.
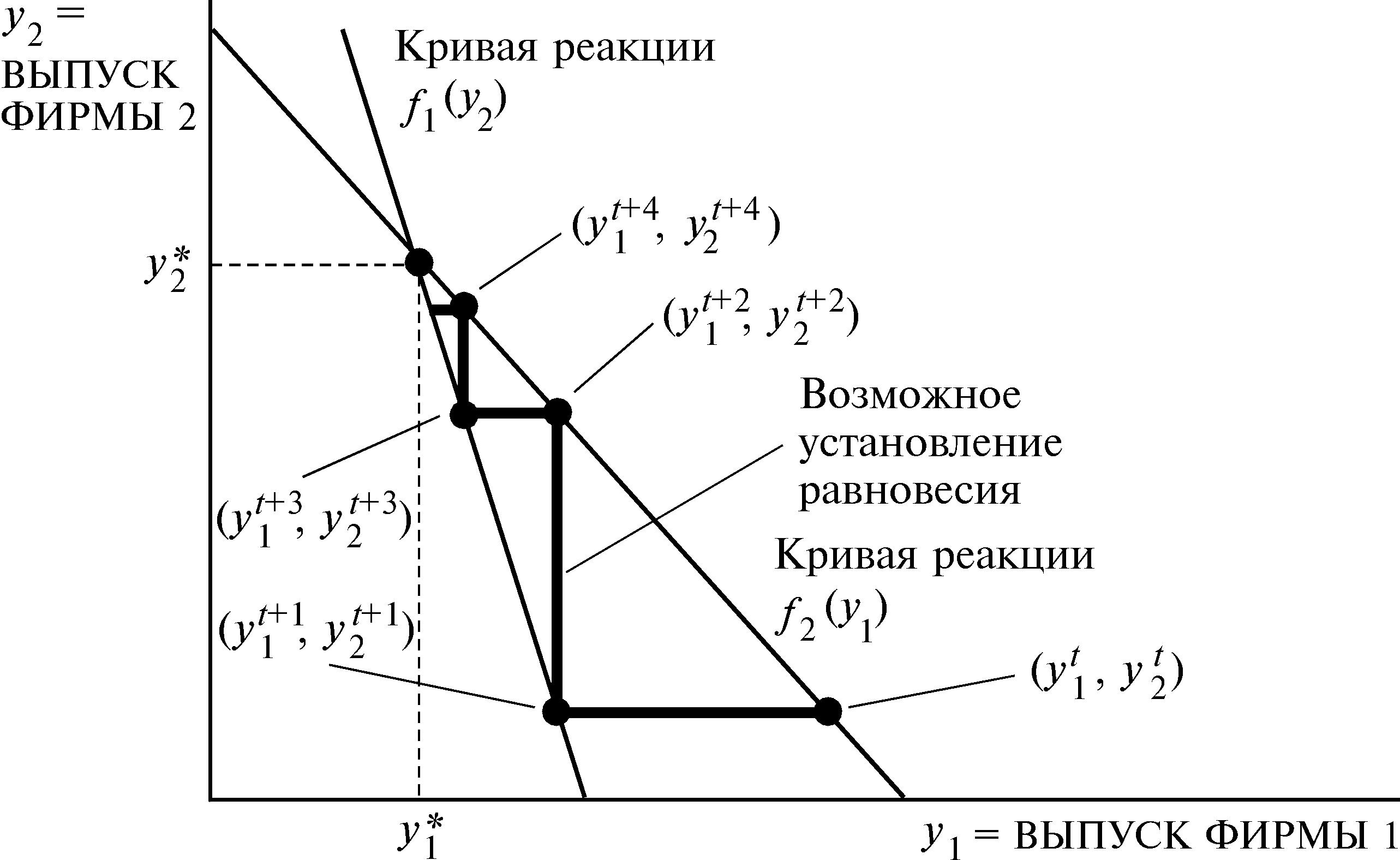
Пример равновесия по Курно приведен на рис.26.2. Равновесие по Курно — это просто пара объемов выпуска, при которых пересекаются две кривые реакции. В такой точке каждая фирма производит объем выпуска, максимизирующий ее прибыль при заданном выборе объема выпуска другой фирмы.
Вспомним случай линейной функции спроса и нулевых предельных издержек, исследовавшийся нами ранее. Как мы видели, тогда функция реакции для фирмы 2 принимает вид
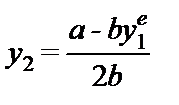 .
.
Поскольку в этом примере фирма 1 ничем не отличается от фирмы 2, ее функция реакции имеет тот же вид:
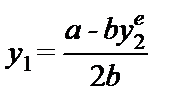 .
.
Эта пара кривых реакции изображена на рис.26.4. Пересечение двух указанных линий дает равновесие по Курно. В этой точке выбор каждой фирмы есть выбор, максимизирующий ее прибыль при данных ожиданиях в отношении поведения другой фирмы, и справедливость ожиданий каждой фирмы в отношении поведения другой подтверждается ее фактическим поведением.
Чтобы получить алгебраическое решение для равновесия по Курно, ищем точку (y1, y2), в которой каждая фирма поступает в соответствии с тем, чего от нее ожидает другая фирма. Мы устанавливаем y 1 = 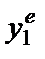 и y 2 =
и y 2 = 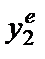 , что дает два следующих уравнения с двумя неизвестными:
, что дает два следующих уравнения с двумя неизвестными:
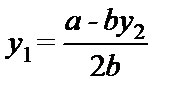 ,
, 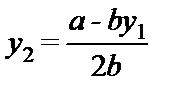 .
.
В данном примере обе фирмы одинаковы, поэтому каждая из них в равновесии будет производить один и тот же объем выпуска. Следовательно, можно подставить y1 = y2 в одно из приведенных выше уравнений, получив при этом
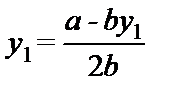 .
.
Решив уравнение для 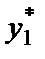 , получаем
, получаем
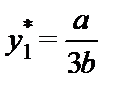 .
.
Так как обе фирмы одинаковы, это означает также, что
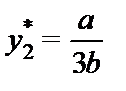
и что общий выпуск отрасли есть 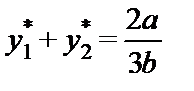 .
.
Установление равновесия
Мы можем воспользоваться рис.26.4, чтобы описать процесс установления равновесия. Предположим, что в момент времени t фирмы производят объемы выпуска (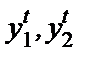 ), которые не обязательно являются равновесными. Если фирма 1 ожидает, что фирма 2 собирается продолжать производить выпуск
), которые не обязательно являются равновесными. Если фирма 1 ожидает, что фирма 2 собирается продолжать производить выпуск 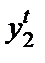 , то в следующем периоде фирма 1 захочет выбрать объем выпуска, максимизирующий ее прибыль с учетом данного ожидания, а именно,
, то в следующем периоде фирма 1 захочет выбрать объем выпуска, максимизирующий ее прибыль с учетом данного ожидания, а именно, 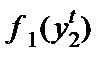 . Следовательно, выбор фирмы 1 в период t + 1 будет задан уравнением
. Следовательно, выбор фирмы 1 в период t + 1 будет задан уравнением
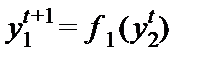 .
.
Фирма 2 может рассуждать таким же образом, поэтому выбор фирмы 2 в следующем периоде будет задаваться уравнением
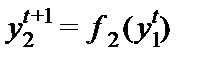 .
.
Эти уравнения описывают, каким образом каждая фирма изменяет свой объем выпуска перед лицом выбора другой фирмы. Рис.26.4 иллюстрирует перемещение точек выпуска двух фирм, подразумеваемое таким поведением. Поясним данный график. Начнем с какой-то точки выпуска (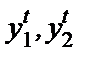 ). При заданном объеме выпуска фирмы 2 фирма 1 в оптимуме предпочтет в следующем периоде произвести
). При заданном объеме выпуска фирмы 2 фирма 1 в оптимуме предпочтет в следующем периоде произвести 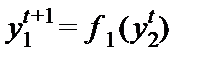 . Мы находим эту точку на графике, перемещаясь по горизонтали влево, пока не дойдем до кривой реакции фирмы 1. Если фирма 2 ожидает, что фирма 1 будет продолжать производить
. Мы находим эту точку на графике, перемещаясь по горизонтали влево, пока не дойдем до кривой реакции фирмы 1. Если фирма 2 ожидает, что фирма 1 будет продолжать производить 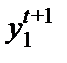 , то ее оптимальным ответом будет решение производить
, то ее оптимальным ответом будет решение производить 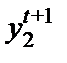 . Находим эту точку, перемещаясь вертикально вверх, пока не дойдем до кривой реакции фирмы 2. Продолжая двигаться вдоль "лестницы", определяем тем самым ряд последовательных точек выбора объемов выпуска двух фирм. В проиллюстрированном нами примере этот процесс приспособления сходится в точке равновесия по Курно. Мы говорим, что в этом случае равновесие по Курно является устойчивым равновесием.
. Находим эту точку, перемещаясь вертикально вверх, пока не дойдем до кривой реакции фирмы 2. Продолжая двигаться вдоль "лестницы", определяем тем самым ряд последовательных точек выбора объемов выпуска двух фирм. В проиллюстрированном нами примере этот процесс приспособления сходится в точке равновесия по Курно. Мы говорим, что в этом случае равновесие по Курно является устойчивым равновесием.
Равновесие по Курно для случая многих фирм
Допустим теперь, что в равновесии по Курно находятся не две, а несколько фирм. Предположим, что каждая фирма имеет определенные ожидания в отношении выбора объемов выпуска другими фирмами отрасли, и попытаемся описать равновесный выпуск.
Допустим, что в отрасли существует n фирм, и обозначим общий выпуск отрасли через  . Тогда условие "предельный доход равняется предельным издержкам" для i-й фирмы есть
. Тогда условие "предельный доход равняется предельным издержкам" для i-й фирмы есть
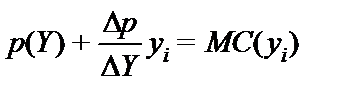 .
.
Вынеся за скобку p(Y) и умножив второй член на Y/Y, можем записать это уравнение как
p (Y) 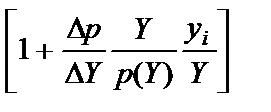 = MC (yi).
= MC (yi).
34. Дуополия Стэкльберга.
В случае лидерства по объему выпуска одна из фирм делает свой выбор раньше другой. Иногда такую модель взаимодействия называют моделью Стэкельберга в честь первого экономиста, который подверг систематическому исследованию взаимодействия по типу "лидер-ведомый".
Модель Стэкельберга часто используется для характеристики отраслей, в которых существует одна доминирующая фирма, или естественный лидер. Обратимся к деталям данной теоретической модели. Предположим, что фирма 1 — лидер и что она решает производить объем выпуска y1. Фирма 2 в ответ на это выбирает объем выпуска y2. Каждая из двух фирм знает, что равновесная цена на рынке зависит от общего произведенного объема выпуска. Воспользуемся обратной функцией спроса p(Y), чтобы выразить равновесную цену как функцию отраслевого выпуска Y = y1 + y2.
Какой объем выпуска следует выбрать лидеру, чтобы максимизировать свою прибыль? Ответ зависит от того, какова, по мнению лидера, будет реакция ведомого на сделанный им выбор. Лидер, по-видимому, должен ожидать, что ведомый также попытается максимизировать прибыль при данном выборе, сделанном лидером. Чтобы лидер мог принять разумное решение в отношении собственного производства, он должен рассмотреть задачу максимизации прибыли ведомого.
Мы предполагаем, что ведомый хочет максимизировать свою прибыль:
max p (y 1 + y 2) y 2 — c 2(y 2).
Прибыль ведомого зависит от выбора объема выпуска лидером, но, с точки зрения ведомого, выпуск лидера предопределен — лидер уже осуществил производство, и ведомый просто считает его объем выпуска постоянным.
Ведомый стремится выбрать такой объем выпуска, при котором предельный доход равен предельным издержкам:
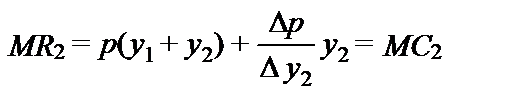 .
.
Предельный доход имеет обычную интерпретацию. Когда ведомый увеличивает выпуск, он увеличивает свой общий доход, продавая больший объем выпуска по рыночной цене. Но он также снижает цену на Dp, а это понижает прибыль, получаемую им на все те единицы выпуска, которые раньше продавались по более высокой цене.
Необходимо отметить следующий важный момент: выбор объема выпуска, максимизирующий прибыль ведомого, будет зависеть от выбора, сделанного лидером. Мы записываем эту взаимосвязь как
y 2 = f 2(y 1).
Функция f 2(y 1) представляет максимизирующий прибыль выпуск ведомого как функцию объема выпуска лидера. Эта функция называется функцией реакции, так как показывает, как будет реагировать ведомый на выбор объема выпуска лидером.
Выведем кривую реакции для простого случая линейной кривой спроса. Здесь функция спроса (обратная) принимает вид p (y 1 + y 2) = a — b (y 1 + y 2). Для удобства примем издержки равными нулю.
Тогда функцию прибыли для фирмы 2 можно записать в виде:
p2(y 1, y 2) = [ a — b (y 1 + y 2)] y 2
p2(y 1, y 2) = ay 2 — by 1 y 2 — 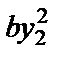 .
.
Можно воспользоваться этим выражением, чтобы провести на рис.26.1 изопрофитные линии. Это линии, описывающие те комбинации y1 и y2, которые приносят фирме 2 постоянный уровень прибыли. Иными словами, изопрофитные линии состоят из всех точек (y1, y2), удовлетворяющих уравнениям вида
ay 2 — by 1 y 2— 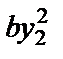 =
=  .
.
Обратите внимание, что по мере движения к изопрофитным линиям, расположенным левее, прибыль фирмы 2 будет возрастать. Это справедливо, потому что если фиксировать выпуск фирмы 2 на некотором уровне, то прибыль фирмы 2 будет увеличиваться по мере уменьшения выпуска фирмы 1. Максимально возможную прибыль фирма 2 получит в ситуации, когда она будет монополистом; иначе говоря, когда фирма 1 предпочтет производить ноль единиц выпуска.
При каждом возможном выборе объема выпуска фирмой 1 фирма 2 стремится выбрать свой собственный объем выпуска таким образом, чтобы как можно больше увеличить свою прибыль. Это означает, что для каждого выбранного y1 фирма 2 выберет такое значение y 2, при котором она окажется на изопрофитной кривой, расположенной левее других (рис.26.1). Эта точка будет удовлетворять обычному условию касания: изопрофитная кривая в точке оптимального выбора должна быть вертикальна. Геометрическое место точек таких касаний описывает кривую реакции фирмы 2 — f 2(y 1).
Чтобы посмотреть, как выглядит данный результат алгебраически, необходимо иметь выражение для предельного дохода, связанного с функцией прибыли для фирмы 2. Это выражение задается следующим образом:
MR 2(y 1, y 2) = a — by 1— 2 by 2.
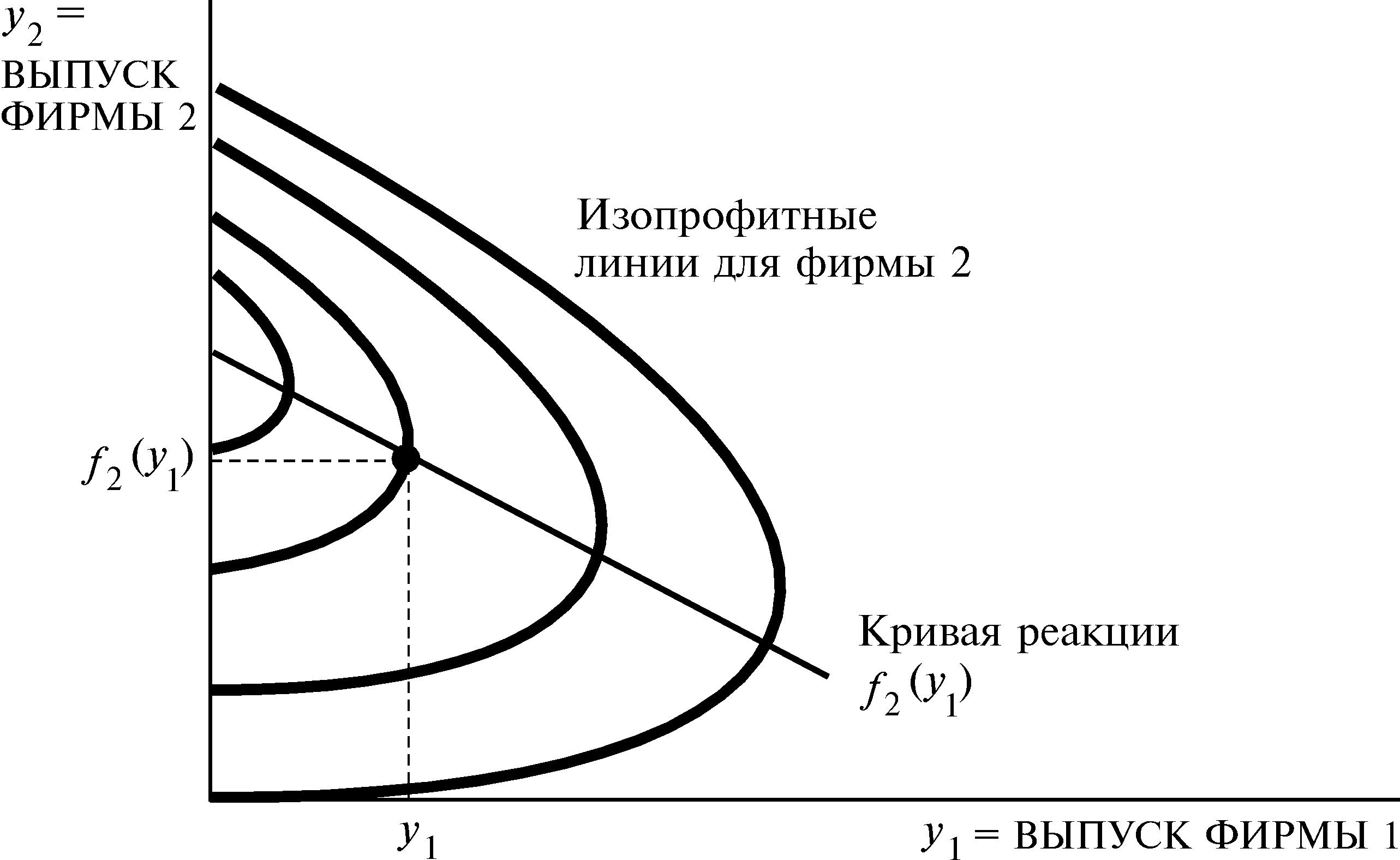
Приравняв предельный доход к предельным издержкам, которые в данном случае равны нулю, получаем уравнение
a — by 1— 2 by 2 = 0,
которое можно решить, выведя при этом кривую реакции фирмы 2:
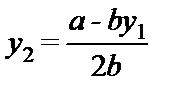 .
.
Эта кривая реакции есть прямая линия, изображенная на рис.26.1.
Обратимся теперь к задаче максимизации прибыли лидера.
Предположительно, лидер также осознает, что его действия оказывают влияние на выбор объема выпуска ведомым. Эта взаимосвязь в краткой форме выражена функцией реакции f 2(y 1). Следовательно, выбирая свой объем выпуска, лидер должен признавать влияние, оказываемое им на ведомого.
Задача максимизации прибыли лидером поэтому принимает вид
max p (y 1 + y 2) y 1 — c 1(y 1)
при y 2 = f 2(y 1).
Подстановка второго уравнения в первое дает
max p [ y 1 + f 2(y 1)] y 1 — c 1(y 1).
Обратите внимание на то, что лидер осознает, что при выборе объема выпуска y 1 общий производимый выпуск составит y1 + f2(y1): его собственный выпуск плюс выпуск, производимый ведомым. Намереваясь изменить объем своего выпуска, лидер должен осознавать влияние, оказываемое им на ведомого. Рассмотрим это применительно к описанной выше линейной кривой спроса. Как мы видели выше, кривая реакции в этом случае задается уравнением
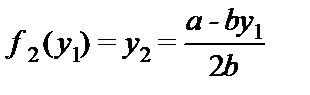 . (26.1)
. (26.1)
Поскольку мы предположили, что предельные издержки равны нулю, прибыль лидера есть
p1(y 1, y 2) = p (y 1 + y 2) y 1 = ay 1 —  — by 1 y 2. (26.2)
— by 1 y 2. (26.2)
Но выпуск ведомого y2 будет зависеть от выбора лидера в соответствии с функцией реакции y2 = f2(y1).
Подставив выражение для y2 из уравнения (26.1) в уравнение (26.2), получаем
p1(y 1, y 2) = ay 1 —  — by 1 f 2(y 1) = ay 1 —
— by 1 f 2(y 1) = ay 1 —  — by 1
— by 1 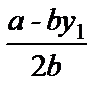 .
.
Упростив это выражение, имеем
p1(y 1, y 2) = 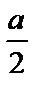 y 1 —
y 1 — 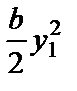 .
.
Предельный доход для этой функции есть
 — by 1.
— by 1.
Приравняв его к предельным издержкам, которые в этом примере равны нулю, и найдя из полученного уравнения y1, получим
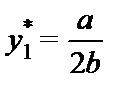 .
.
Чтобы найти выпуск ведомого, просто подставляем 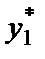 в функцию реакции:
в функцию реакции:
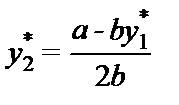
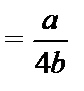 .
.
Эти два уравнения дают общий отраслевой выпуск 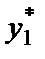 +
+ 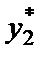 = 3 a /4 b.
= 3 a /4 b.
Решение по Стэкльбергу можно также проиллюстрировать графически с помощью изопрофитных кривых, представленных на рис.26.2. (Этот рисунок иллюстрирует также равновесие по Курно). Здесь мы изобразили кривые реакции для обеих фирм и изопрофитные кривые для фирмы 1. Изопрофитные кривые для фирмы 1 имеют ту же общую форму, что и изопрофитные кривые для фирмы 2; они просто повернуты на 90°. Более высокая прибыль для фирмы 1 связывается с более низкими изопрофитными кривыми, так как прибыль фирмы 1 будет расти по мере уменьшения выпуска фирмы 2.
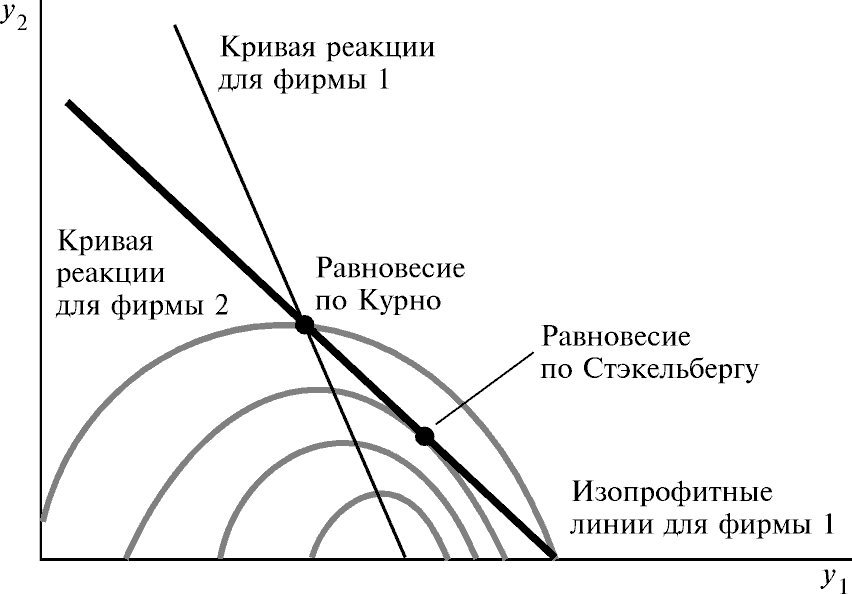
| Равновесие по Стэкльбергу. Фирма 1, лидер, выбирает ту точку на кривой реакции фирмы 2, в которой эта кривая касается самой низкой изопрофитной линии фирмы 1 из возможных, тем самым обеспечивая фирме 1 самую высокую прибыль из возможных. | Рис. 26.2 |
Фирма 2 ведет себя как ведомый, а это означает, что она будет выбирать выпуск, перемещаясь вдоль своей кривой реакции, f2(y1). Следовательно, фирма 1 хочет выбрать такую комбинацию выпуска на кривой реакции, которая дает ей наивысшую возможную прибыль. Но получение наивысшей возможной прибыли означает выбор такой точки на кривой реакции, в которой эта кривая касается самой низкой изопрофитной линии, как показано на рис.26.2. Что кривая реакции должна быть касательной к изопрофитной линии в данной точке — следует из обычной логики максимизации.
35. Дуополия Бертрана.
Согласно предпосылке описанной выше модели Курно фирмы выбирают объемы выпуска, оставляя определение цены за рынком. Согласно другому подходу фирмы устанавливают цены на свой выпуск, оставляя за рынком определение объемов продаж. Эта модель известна модель олигополии Бертрана.
Выбирая цену, фирма должна предвидеть цену, устанавливаемую другой фирмой отрасли. Так же, как в случае равновесия по Курно, мы хотим найти пару цен такую, что каждая из них является выбором, максимизирующим прибыль при заданном выборе цены другой фирмой. Как выглядит равновесие по Бертрану? В ситуации, когда фирмы продают, как мы предположили, одинаковые продукты, структура равновесия по Бертрану на самом деле очень проста. Это равновесие оказывается конкурентным равновесием в точке, где цена равна предельным издержкам. Сначала обратим внимание на то, что цена никогда не может быть меньше предельных издержек, поскольку иначе каждая из фирм увеличила бы свою прибыль, начав производить меньше. Поэтому рассмотрим случай, когда цена больше предельных издержек. Предположим, что обе фирмы продают выпуск по некоторой цене  , которая выше предельных издержек. Рассмотрим позицию фирмы 1. Если она снизит свою цену на любую малую величину e и если другая фирма сохранит свою цену на уровне
, которая выше предельных издержек. Рассмотрим позицию фирмы 1. Если она снизит свою цену на любую малую величину e и если другая фирма сохранит свою цену на уровне  , то все потребители захотят покупать продукт у фирмы 1. Снизив цену на произвольно малую величину, эта фирма сможет увести у фирмы 2 всех покупателей.
, то все потребители захотят покупать продукт у фирмы 1. Снизив цену на произвольно малую величину, эта фирма сможет увести у фирмы 2 всех покупателей.
Если фирма 1 действительно думает, что фирма 2 назначит цену  , большую, чем предельные издержки, ей всегда будет выгодно снизить цену до
, большую, чем предельные издержки, ей всегда будет выгодно снизить цену до  — e. Но фирма 2 может рассуждать точно так же, Следовательно, в равновесии не может существовать никакая цена, которая была бы выше предельных издержек; единственно возможное равновесие — конкурентное.
— e. Но фирма 2 может рассуждать точно так же, Следовательно, в равновесии не может существовать никакая цена, которая была бы выше предельных издержек; единственно возможное равновесие — конкурентное.
Если, однако представить себе модель Бертрана как модель конкурентных торгов, результат этот приобретет больший смысл. Допустим, что одна из фирм участвует в торгах, назначая цену выше предельных издержек. Тогда другая фирма всегда может получить прибыль, сбивая эту цену. Отсюда следует, что единственная цена, "сбивания" которой не может ожидать ни одна из фирм, есть цена, равная предельным издержкам.
Часто можно наблюдать, что в результате конкурентных торгов с участием фирм, не готовых к сговору, устанавливаются цены, много ниже тех, к которым можно было бы придти каким-то другим способом. Это явление есть не что иное как пример логики конкуренции по Бертрану.
Поиск по сайту: