Решение типовых примеров. Пример 1: заемщик получил кредит на 6 месяцев под 80 % годовых (процентная ставка простая) с условием вернуть 2 тыс.р

Пример 1: заемщик получил кредит на 6 месяцев под 80 % годовых (процентная ставка простая) с условием вернуть 2 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

Решение: очевидно требуется определить, сколько стоят 2 тыс.р., полученные через 6 месяцев сегодня, то есть найти современную стоимость кредита. Применив операцию дисконтирования, получим

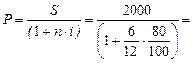1428,57.

Дисконт по формуле (1.3) равен

.

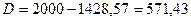Пример 2: на какой срок необходимо вложить 1 тыс.р. в банк, чтобы получить 1,4 тыс.р. Годовая простая процентная ставка равна 15 %.

Решение: из формулы (1.1) выразим n. Получим

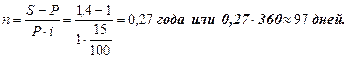
Пример 3: в контракте предусматривается погашение обязательства в сумме 10 тыс.р. через 46 дней. Первоначальная сумма долга – 9 тыс.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки. Определить доходности, если срок погашения через 20 дней.

Решение:

из формулы (1.1)

.

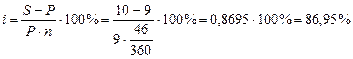Пример 4: какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 20 тыс.р.: а) за 6 месяцев; б) за 2 года; в) за 1000 дней?

Решение: а) учитывая, что срок выражен в месяцах, воспользовавшись формулой (1.2), получим

;

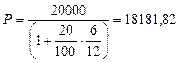б) ; в) .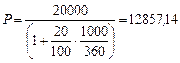

Варианты задания № 1

1. Заемщик получил кредит на 6 месяцев под 80 % годовых (используется простая процентная ставка) с условием вернуть
3 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

2. На какой срок необходимо вложить 1 тыс.р. в банк, чтобы получить 1,4 тыс.р. Годовая процентная ставка (простая) равна 15 %?

3. В контракте предусматривается погашение обязательства в сумме 10 млн.р. через 46 дней. Первоначальная сумма долга – 9 млн.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки и простой учетной ставки (К=360). Определить доходности, если срок погашения через 20 дней, 60 дней?

4. Какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 20 тыс.р.: а) за 6 месяцев; б) за 2 года; в) за 1000 дней? Процентная ставка равна 20 %.

5. Договор предусматривает следующую схему начисления простых процентов: за первый год – 60 %, в каждом последующем полугодии ставка повышается на 10 %. Требуется определить коэффициент наращения за 2,5 года.

6. Договор предусматривает следующую схему начисления простых процентов: за первый год – 40 %, в каждом последующем полугодии ставка повышается на 15 %. Требуется определить коэффициент наращения за 3 года.

7. Заемщик получил кредит на 12 месяцев под 20 % годовых (используется простая процентная ставка) с условием вернуть 4 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

8. На какой срок необходимо вложить 2 тыс.р. в банк, чтобы получить 2,5 тыс.р. Годовая процентная ставка (простая) равна 25 %?

9. В контракте предусматривается погашение обязательства в сумме 10 млн.р. через 46 дней. Первоначальная сумма долга – 9 млн.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки и простой учетной ставки (К=360). Определить доходности, если срок погашения через 20 дней, 60 дней?

10. Какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 10 тыс.р.: а) за 9 месяцев; б) за 2 года; в) за 1200 дней? Процентная ставка равна 20 %.

11. В контракте предусматривается погашение обязательства в сумме 15 тыс.р. через 38 дней. Первоначальная сумма
долга – 14 тыс.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки и простой учетной ставки (К=360). Определить доходности, если срок погашения через 20 дней, 6 месяцев?

12. Договор предусматривает следующую схему начисления простых процентов: за первый год – 40 %, в каждом последующем полугодии ставка повышается на 5 %. Требуется определить коэффициент наращения за 2 года.

13. Заемщик получил кредит на 8 месяцев под 15 % годовых (используется простая процентная ставка) с условием вернуть
4 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

14. В контракте предусматривается погашение обязательства в сумме 10 тыс.р. через 55 дней. Первоначальная сумма долга – 9,5 тыс.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки и простой учетной ставки (К=360). Определить доходности, если срок погашения через 30 дней, 6 месяцев?

15. Заемщик получил кредит на 5 месяцев под 45 % годовых (используется простая процентная ставка) с условием вернуть
5 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

16. На какой срок необходимо вложить 1 тыс.р. в банк, чтобы получить 2 тыс. Годовая процентная ставка (простая) равна
35 %?

17. Договор предусматривает следующую схему начисления простых процентов: за первый год – 30 %, в каждом последующем полугодии ставка повышается на 15 %. Требуется определить коэффициент наращения за 3 года.

18. На какой срок необходимо вложить 2,5 тыс.р. в банк, чтобы получить 3,4 тыс. Годовая процентная ставка (простая) равна 15 %?

19. Заемщик получил кредит на 6 месяцев под 65 % годовых (используется простая процентная ставка) с условием вернуть
5 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

20. На какой срок необходимо вложить 1 тыс.р. в банк, чтобы получить 1,5 тыс. Годовая процентная ставка (простая) равна 20 %?

21. Какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 40 тыс.р.: а) за 6 месяцев; б) за 2 года; в) за 1200 дней. Процентная ставка равна 20 %.

22. Договор предусматривает следующую схему начисления простых процентов: за первый год – 40 %, в каждом последующем полугодии ставка повышается на 10 %. Требуется определить коэффициент наращения за 4 года.

23. Заемщик получил кредит на 6 месяцев под 45 % годовых (используется простая процентная ставка) с условием вернуть
12 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

24. Какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 30 тыс.р.: а) за 3 месяца; б) за 2 года; в) за 900 дней? Процентная ставка равна 20 %.

25. На какой срок необходимо вложить 7 тыс.р. в банк, чтобы получить 8 тыс. Годовая процентная ставка (простая) равна
35 %?

26. Какую сумму должен внести инвестор сегодня под простые проценты, чтобы накопить 500$: а) за 6 месяцев; б) за 2 года; в) за 1000 дней? Процентная ставка равна 20 %.

27. Договор предусматривает следующую схему начисления простых процентов: за первый год – 34 %, в каждом последующем полугодии ставка повышается на 10 %. Требуется определить коэффициент наращения за 4 года.

28. В контракте предусматривается погашение обязательства в сумме 10 тыс.р. через 40 дней. Первоначальная сумма долга – 9 тыс.р. Необходимо определить доходность ссудной операции для кредитора в виде годовой простой процентной ставки и простой учетной ставки (К=360). Определить доходности, если срок погашения через 20 дней, 60 дней?

29. На какой срок необходимо вложить 34 тыс.р. в банк, чтобы получить 36 тыс.р. Годовая процентная ставка (простая) равна 25 %?

30. Заемщик получил кредит на 6 месяцев под 40 % годовых (используется простая процентная ставка) с условием вернуть
3 тыс.р. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

2. КОНТУР ФИНАНСОВОЙ ОПЕРАЦИИ. ПОГАШЕНИЕ ЗАДОЛЖЕННОСТИ ЧАСТЯМИ С ПОМОЩЬЮ АКТУАРНОГО МЕТОДА

2.1. Краткие сведения, необходимые для выполнения
задания № 2

D1

Необходимым условием финансовой или кредитной операции в любой ее форме является сбалансированность вложений и отдачи. Понятие сбалансированности удобно пояснить на графике. Пусть сумма в размере D 0 выдана на срок T. На протяжении этого срока в счет погашения задолженности производятся допустим, два платежа: R 1 и R 2, а в конце срока выплачивается остаток задолженности в сумме R 3 (рис. 1). Очевидно, что на интервале t 1 задолженность возрастает (в силу начисления процентов) до величины D 1. В конце этого периода в счет погашения задолженности выплачивается сумма R 1, долг уменьшается до K 1 и т.д. Заканчивается операция получением кредитором в окончательный расчет суммы R 3. В этот момент задолженность должна быть равна нулю. Назовем такой график контуром финансовой операции (рис. 2).

 

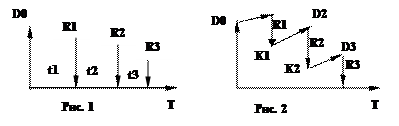Сбалансированная операция обязательно имеет замкнутый контур, то есть последняя выплата полностью покрывает остаток задолженности.

Краткосрочные обязательства погашаются иногда с помощью последовательности частичных платежей. В этом случае надо решить вопрос о том, какую сумму надо брать за базу для расчета процентов и каким путем определять остаток задолженности. Одним из методов решения этой задачи является актуарный метод. Этот метод применяется в основном в операциях со сроком более одного года.

Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Такое поступление приплюсовывается к следующему платежу. В дальнейшем мы будем выплачивать суммы, большие начисленных процентов. В дальнейшем мы будем выплачивать платежи, большие начисляемых процентов.

Для случая, показанного на рис. 2, получим следующие расчетные формулы:

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

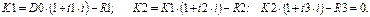
Поиск по сайту:

---