 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Приклад 2. Створення контрольної карти часток невідповідностей( р – карти )
На великому підприємстві автосервісу хочуть оцінити процес розрахунків із постачальниками запчастин, оскільки від вчасності оплати за товари залежить надходження нових партій, отже, і товарооборот підприємства. Для цього досліджують кількість рахунків на певний день, які не були вчасно оплачені. Кількість рахунків до оплати кожного дня різна. Тому кількість вчасно не виконаних розрахунків вирішено визначати як частку від загальної кількості рахунків на поточний день. У результаті виконаного протягом місяця дослідження, тобто за 22 робочі дні, отримані наведені в табл. 6 результати.
Результати процесу оплати рахунків Таблиця 6.
| День | Загальна кількість рахунків | Кількість неоплачених рахунків | Частка |
| 0,076 | |||
| 0,029 | |||
| 0,044 | |||
| 0,051 | |||
| 0,110 | |||
| 0,056 | |||
| 0,088 | |||
| 0,082 | |||
| 0,046 | |||
| 0,169 | |||
| 0,041 | |||
| 0,064 | |||
| 0,062 | |||
| 0,030 | |||
| 0,059 | |||
| 0,029 | |||
| 0,088 | |||
| 0,056 | |||
| 0,069 | |||
| 0,173 | |||
| 0,070 | |||
| 0,070 | |||
| Разом | 0,072 |
На основі цих даних вирішено розробити карту часток невчасно оплачених рахунків (контрольну карту часток невідповідностей: р- карту). Невідповідністю є невчасно сплачений рахунок.
Визначаємо частки сплачених рахунків у кожній вибірці за формулою:
 , (39)
, (39)
де dі -кількість невідповідностей у вибірці і (кількість неоплачених рахунків за день і); nі - обсяг вибірки і (загальна кількість рахунківза день і); рі – частки невідповідностей у вибірці і (частка неоплачених рахунків за день і).
Результати обчислення представлені в табл.6.
Стандартно встановленого значення для допустимої частки неоплачених рахунків немає, тому положення центральної лінії контрольної карти часток невідповідностей за відсутності стандартного значення для процесу встановлюється на основі загальної середньої частки невідповідностей  і розраховується за формулою
і розраховується за формулою
ЦЛ = 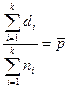 , (40)
, (40)
де  - загальна кількість невідповідностей (загальна кількість неоплачених рахунків за період перевірки);
- загальна кількість невідповідностей (загальна кількість неоплачених рахунків за період перевірки);  - загальна кількість рахунків за весь перевірений період; k - кількість досліджених вибірок (кількість днів за період перевірки);
- загальна кількість рахунків за весь перевірений період; k - кількість досліджених вибірок (кількість днів за період перевірки);  - загальна середня частка невідповідностей (загальна середня частка неоплачених рахунків).
- загальна середня частка невідповідностей (загальна середня частка неоплачених рахунків).
Середня частка невчасно сплачених рахунків становитиме відповідно до (40):
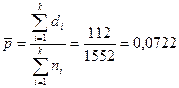 .
.
Отже, центральна лінія контрольної карти часток розташована на рівні ЦЛ=0,072.
Оскільки обсяг рахунків до оплати кожного дня є різним, це значить, що обсяг вибірок, які досліджуються, не є постійним, тому змінюватимуться і контрольні межі. В такій ситуації найточнішим буде обчислення контрольних меж окремо для кожного дня вибірки. При цьому межі встановлюються за формулами
ВКМ(р)=  , (41)
, (41)
НКМ(р)= 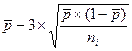 , (42)
, (42)
де nі – обсяг вибірки і;  - загальна середня частка невідповідностей.
- загальна середня частка невідповідностей.
Результати розрахунків контрольних меж наведено в таблиці 7.
Таблиця 7.
Дані для побудови контрольної карти часток неоплачених рахунків
| День | Частка вчасно неоплачених рахунків | ВКМ | НКМ |
| 0,076 | 0,160 | -0,015 | |
| 0,029 | 0,166 | -0,022 | |
| 0,044 | 0,166 | -0,022 | |
| 0,051 | 0,160 | -0,015 | |
| 0,110 | 0,163 | -0,019 | |
| 0,056 | 0,164 | -0,019 | |
| 0,088 | 0,175 | -0,031 | |
| 0,082 | 0,163 | -0,019 | |
| 0,046 | 0,168 | -0,024 | |
| 0,169 | 0,161 | -0,016 | |
| 0,041 | 0,162 | -0,018 | |
| 0,064 | 0,160 | -0,016 | |
| 0,062 | 0,168 | -0,024 | |
| 0,030 | 0,167 | -0,023 | |
| 0,059 | 0,166 | -0,022 | |
| 0,029 | 0,166 | -0,021 | |
| 0,088 | 0,166 | -0,022 | |
| 0,056 | 0,164 | -0,020 | |
| 0,069 | 0,164 | -0,019 | |
| 0,173 | 0,158 | -0,014 | |
| 0,070 | 0,164 | -0,020 | |
| 0,070 | 0,175 | -0,031 |
Всі розраховані значення нижньої контрольної межі менші 0, тому на карту буде нанесено значення НКМ=0.
Контрольна карта часток вчасно не оплачених рахунків, представлена на рис.17.
Контрольна карта показує, що процес розрахунків є статистично нестабільним. У 10-й та 20-й за порядком робочі дні на процес розрахунків впливає певна особлива причина надмірної варіації. Аналіз показав, що ці дні – п’ятниця, кінець робочого тижня. В цей день у банку, через який здійснюються розрахунки, скорочений робочий день, тому значну кількість рахунків не встигають оплатити. Керівництво вирішило доповнити бухгалтерську програму модулем, який би попереджав бухгалтерів, що кінцева дата оплати рахунку припадає на п’ятницю, тому рахунок краще оплатити в четвер.
Оскільки особливу причину вдалося визначити, то спостереження, які відповідали сигналам контрольної карти, можна не враховувати, перерахувавши характеристики контрольної карти для моніторингу процесу вчасності виконання розрахунків.
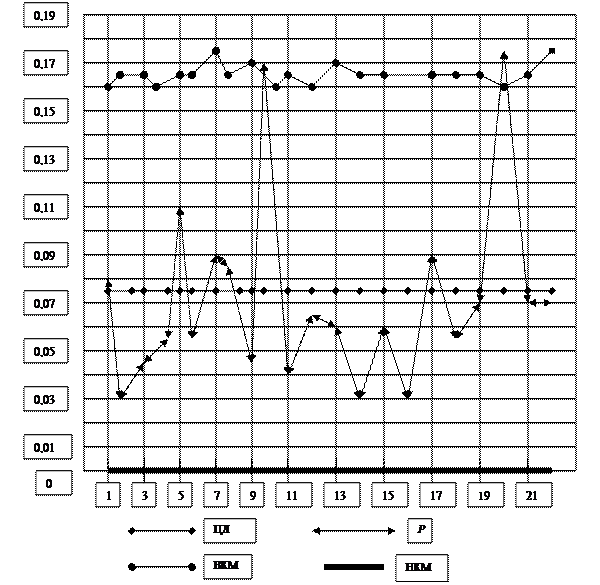
Рис.17. Контрольна карта часток вчасно не оплачених рахунків.
Після вилучення спостережень 10 і 20 середня частка становить згідно (40)
 .
.
Контрольна карта з перерахованими, на основі нової середньої частки, контрольними межами наведена на рис.18.
Отже, центральна лінія контрольної карти часток така: ЦЛ=0,061.
Контрольна карта на рис.18 показує, що процес розрахунків став статистично стабільним. Визначену частку невчасно оплачених рахунків можна використовувати як стандартне значення для подальшого моніторингу стабільності процесу оплати рахунків.

Рис.18. Контрольна карта часток невчасно виконаних розрахунків після вжиття заходів для стабілізації системи.
Завдання для самостійної роботи.
Використовуючи приклади побудови контрольних карт (приклад 1,2), розробити контрольну u- картусередньої кількості невчасно оплачених рахунків від загальної кількості рахунків для оплати на підприємстві автосервісу. Дані для розрахунків взяти із таблиці 6.
6.4. Діаграма Парето
Відомий працями з розподілу багатства серед населення країн, італійський економіст Вільфредо Парето (1848 – 1923) виявив, що в Англії в ХІХ столітті 20% населення володіли 80 % багатств. Подібну ситуацію в приблизних пропорціях можна спостерігати в усіх розвинутих країнах сучасного світу. Таким чином, принцип Парето полягає в тому, що аналізуючи показники, які характеризують групу предметів чи людей, можна констатувати, що їх мала кількість представляє собою велику значимість, тоді, як велика кількість, яка залишається, має малу значимість.
Наприклад, дуже часто мала кількість відсотків клієнтів підприємства приносить левову частку доходів.
Принцип Парето використовують під час організації постачання запасних матеріалів за методом АВС, за яким виділяються мало чисельні по номенклатурі, але важливі по витрачанню та вартості запасні частини, на які припадає більша частина грошових ресурсів, укладених у запаси (група А). Цій групі приділяють більше уваги. Група В включає запасні частини середнього попиту та не дуже значної сукупної вартості, а група С – запасні частини багато чисельної номенклатури, але малого попиту.
В сфері управління якістю принцип Парето проявляється в тому, що при великій кількості обладнання та виконавців причиною браку, звичайно, є лише деякі з них, які й можуть бути виявлені за допомогою побудови діаграми Парето.
Діаграма Парето є графічним зображенням даних, де на осях координат відкладаються види проблем, або класи об’єктів (тип дефектів), ранжовані в порядку значимості, що зменшується, та величини значимості проблем (кількість дефектів, відповідний до проблеми процент браку, вартість браку тощо). Різні класи проблем чи об’єктів зображуються прямокутниками, висота яких пропорційна ступеню їх значимості. Часто на діаграмі наносять ламану лінію, яка показує сукупну значимість різних класів проблеми,
починаючи з найбільш значимого.
Приклад діаграми Парето показаний на рис.19.
Звичайно використовують два типи діаграм: частот виникнення проблем та вартостей наслідків проблем. У діаграмах першого типу по вертикальній осі відкладають частоту виникнення проблеми (кількість випадків, процент від загальної кількості випадків). У діаграмах другого типу по вертикальній осі відкладають вартість браку у абсолютній величині або в процентах від загальної вартості браку (рис.19).

Рис. 19. Діаграма Парето.
Приклад. Побудуємо діаграму Парето за даними з табл. 8. Ця діаграма представлена на рис.20.
Таблиця 8.


Рис. 20. Діаграма Парето причин відмов автомобілів.
Завдання для самостійної роботи
За таблицею даних, які використовуються для локалізації дефектів двигуна автомобіля (табл.9), побудувати діаграму Парето.
Таблиця 9.
Кількість відмов у залежності від місця виникнення

6.5. Діаграма «причини-наслідки» (Ішикави)
Варіація характеристик продукту може мати багато причин. Коли констатується статистичний сигнал, який свідчить про наявність якогось спеціального чинника, що є причиною браку, необхідно відшукати і усунути цю причину.
Діаграма «причини-наслідки» - це графічна ілюстрація процесу виявлення причин неякості [11].
Загальний вигляд діаграми Ішикави представлений на рис. 21.

Рис.21. Діаграма Ішикави (діаграма причин та наслідків).
Процес виявлення причин неякості виконується групою в такій послідовності:
1) Визначають та описують з максимальною точністю продукт, процес або подію, які необхідно вивчити, характеристики, які необхідно отримати;
2) Складають список усіх можливих причин варіації результату;
3) Виділяють головні загальні причини, які прямо впливають на якість. Групують всі непрямі причини по групах та підгрупах, що входять у групи;
4) Креслять діаграму «причини-наслідки» на великому аркуші. Діаграма доповнюється у міру вивчення проблеми.
Така діаграма є візуальною підтримкою для роботи в групі. Члени групи збирають інформацію та дані, необхідні для вирішення проблеми. Якщо цього виявляється недостатньо для знайдення рішення, то група збирається ще раз через деякий час, маючи нову інформацію та нові дані. Так робиться доти, поки не буде знайдена основна причина варіації характеристики, що досліджується.
Потрібно відмітити, що не діаграма приносить рішення. Вона тільки допомагає добре поставити проблему, що дуже важливо на початку роботи. Після чого кожен член групи або відділу, які займаються якістю пропонує гіпотези, які перевіряються за допомогою статистичних методів дослідження. Після цього виробляються рішення щодо усунення причин неякості.
Приклад. Приклад діаграми причин та наслідків(Ішикави), яка розроблена у французькій компанії SFA Assistance для поліпшення якості телефонного спілкування, що є основою виробничої діяльності компанії, яка займається організацією надання допомоги клієнтам, які захворіли або потрапили в аварію у дорозі, показаний на рис. 22. На основі аналізу цієї діаграми в компанії складені стандарти телефонного спілкування, яких має дотримуватись весь персонал. Виконання цих стандартів контролює відділ якості компанії.
Завдання для самостійної роботи.
Фірма Renault провела дослідження з метою визначення мотивів поведінки клієнтів під час вибору СТО для купівлі автомобіля та подальшого його обслуговування, результати якого наведені в табл. 10. Побудувати діаграму причин та наслідків (Ішикави) для визначення причин втрати клієнтами мотивів вибору СТО.
Таблиця 10.
Значимість мотивів вибору СТО для купівлі автомобіля та його обслуговування (на 100 власників автомобілів Renault)


Рис. 22. Приклад діаграми причин та наслідків (Ішикави) для вияснення факторів, які впливають на якість телефонного спілкування.
Приклад. На рис.23 приведена Діаграма Ішикави (причин та наслідків) із факторами, що викликають брак двигуна після ремонту. До центральної стрілки, яка показує об’єкт аналізу, підводять великі первинні стрілки, які позначають групи факторів, що впливають на об’єкт аналізу. Далі до кожної стрілки підводять стрілки другого, третього і т.п. порядку до тих пір, поки на діаграму не будуть нанесені всі стрілки, що позначають фактори, які здійснюють помітний вплив на об’єкт аналізу в конкретній ситуації.

Рис.23. Діаграма Ішикави (причин та наслідків) для визначення факторів браку двигуна після ремонту.
6.6. Діаграми кореляції
Діаграма кореляції є графіком, який характеризує взаємозв’язок між двома величинами А і Б (рис. 24).
Для побудови діаграми кореляції спочатку збирають дані щодо пар величин А і Б. Необхідно мати не менш як 30 пар даних. Після цього на проградуйованих осях відкладають значення величин А і Б для кожної пари та позначають точкою перетин цих координат. Звичайно, параметр, що відповідає причині, відкладають на горизонтальній осі, а наслідку – на вертикальній осі.
Деякі кореляції можна легко бачити на діаграмі. У цьому випадку розташування точок має дуже витягнутий характер. У разі відсутності кореляції між двома параметрами А і Б зона розташування точок має вигляд кола.
Але в усіх випадках існує тест (метод медіан) для виявлення наявності кореляції між двома параметрами. Для дослідження необхідно провести вертикальну та горизонтальну медіани розподілу. Медіани ділять кількість точок навпіл по горизонталі та вертикалі.
Медіани розділяють діаграму кореляції на чотири зони, позначені номерами 1, 2, 3 та 4 (рис. 24). Підраховують кількість точок у кожній зоні (не враховують точки, які знаходяться на медіанах). Потім вносять точки у таблицю.
Складають кількість точок у зонах 1 і 3, 2 і 4. Після цього складають два отриманих числа. Результат повинен дорівнювати кількості n точок на діаграмі, за винятком точок на медіанах.
На рис. 24 наведені граничні тестові дані залежно від кількості точок n. (при α = 0.05 – коефіцієнт ризику становить 5 %).
Якщо найменший результат серед (1 + 3) та (2 + 4) є менший за граничний з таблиці, то кореляція існує, у протилежному випадку вона відсутня.
У прикладі на рис. 24 найменша сума по діагоналях квадрата дорівнює 4, кількість точок n = 22. Цій кількості точок відповідає гранична величина 5, яка є більшою за найменшу суму 4, тобто існує кореляція між величинами А і Б.
Таблиця 11.
Граничні значення тесту на кореляцію
| n | lim | n | lim | n | lim | n | lim |

Рис. 24. Діаграма кореляції.
Шість видів діаграм кореляції, які широко використовуються, представлені на рис.(25 - 28). Вивчаючи ці види діаграм, можна зрозуміти залежність між зібраними наборами даних, яким змінам буде піддаватись один із параметрів під час певних змін іншого.При наявності кореляційного зв’язку причинний фактор здійснює дуже важливий вплив на характеристику, тому втримуючи даний фактор під контролем можна досягнути стабільності характеристики. Можна також визначити рівень контролю, який необхідний для показника якості.
При прямій кореляції під час збільшення Х на діаграмі У також буде збільшуватись. В цьому випадку при здійсненні контролю за причинним фактором Х характеристика У буде залишатися стабільною. Легка пряма кореляція означає, що при збільшенні Х збільшується також і У, однак розсіювання У велике по відношенню до певного значення Х. При такому контролі причинного фактора Х можна лише до певного рівня тримати під контролем характеристику У, і також необхідно приймати до уваги інші фактори, які впливають на У.
Спостерігаючи за оберненою (від’ємною) кореляцією, можна стверджувати, що при збільшенні причинного фактора Х характеристика У зменшується. При легкій оберненій кореляції, коли при зростанні Х зменшується У, при цьому фіксованому значенню Х властиве певне розсіювання значення У.
Можливі випадки відсутності кореляції, коли будь-якої вираженої залежності між Х і У не спостерігається. В цьому випадку необхідно продовжувати пошук факторів, які корелюватимуться з У, виключивши з цього пошуку фактор Х.
Між параметрами Х і У можливі також випадки криволінійної кореляції, якщо при цьому діаграму розсіювання можна розділити на ділянки, які мають прямолінійний характер. При цьому досліджують кожну ділянку окремо. 
Рис. 25.Діаграми прямої кореляції (а) та легкої прямої кореляції (б).

Рис. 26. Діаграми оберненої кореляції (а) та легкої оберненої кореляції (б).
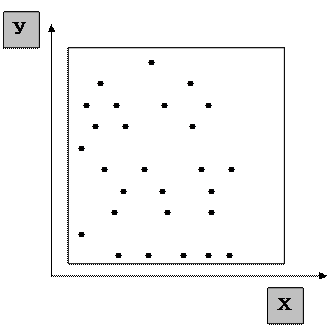

Рис. 27. Діаграма відсутності кореляції. Рис. 28. Діаграма криволінійної кореляції.
Існують різні методи оцінки наявності та ступеня кореляційної залежності(міри щільності зв’язку) двох ознак якості. Одним із них являється метод визначення коефіцієнта кореляції Пірсона r:
 , (43)
, (43)
або  (44)
(44)
Коефіцієнт кореляції змінюється в межах  [-1; +1],
[-1; +1],  . Чим більше його абсолютне значення, тим сильнішим є зв'язок між фактором та ознакою. Зокрема, при
. Чим більше його абсолютне значення, тим сильнішим є зв'язок між фактором та ознакою. Зокрема, при  зв'язок вважається значним; при
зв'язок вважається значним; при 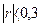 - зв'язок випадковий, несуттєвий; при
- зв'язок випадковий, несуттєвий; при  - потрібно спеціально оцінити надійність зв’язку.
- потрібно спеціально оцінити надійність зв’язку.
При значеннях більших 0 – зв'язок прямий, при значеннях менше 0 – зв'язок зворотній. При r < 0 із зростанням хі значення уі падають; при r > 0 із зростанням хі значення уі збільшуються.
Завдання для самостійної роботи. На рис. 29 представлена діаграма кореляції згідно приведених даних, що в табл. 12. Визначити вид кореляційної залежності та коефіцієнт кореляції Пірсона.

Рис. 29. Діаграма кореляції для діаметра деталі.
1 – діаметр деталі після обробки, мм; 2 – діаметр деталі до обробки, мм.
В кожному із чотирьох квадрантів, що утворилися в результаті розподілу діаграми розсіювання вертикальною і горизонтальною медіанами підрахували число точок:
n1, n2, n3, n4 відповідно.
n (+) = n1 + n3 = 9+9 =18.
n (-) = n2 + n4 = 2+2 =4.
k = n(+) + n(-) = 18 +4 = 22.
Якщо менше із чисел n(+), n(-) виявляється рівним або менше табличного кодового значення(табл.11), то тоді кореляційна залежність має місце.
Оскільки n(+) > n(-), то означає, що кореляція має пряму залежність. Інакше – зворотня кореляція (n(+) < n(-)).
Таблиця12.
Значення діаметра деталі (мм) до та після обробки
| № | До обробки, х | Після обробки, у | № | До обробки, х | Після обробки, у |
| 1 | 6,8 | 6,1 | 14 | 7,5 | 7,1 |
| 2 | 7,1 | 6,7 | 15 | 7,8 | 7,0 |
| 3 | 6,5 | 6,3 | 16 | 6,8 | 6,9 |
| 4 | 7,8 | 7,1 | 17 | 7,3 | 7,3 |
| 5 | 7,5 | 7,4 | 18 | 7,3 | 6,9 |
| 6 | 8,5 | 7,6 | 19 | 8,3 | 7,6 |
| 7 | 8,8 | 8,2 | 20 | 7,2 | 7,3 |
| 8 | 7,0 | 6,4 | 21 | 7,3 | 7,0 |
| 9 | 7,4 | 6,8 | 22 | 5,1 | 7,9 |
| 10 | 6,5 | 6,0 | 23 | 7,9 | 6,9 |
| 11 | 7,8 | 6,8 | 24 | 7,8 | 7,1 |
| 12 | 9,2 | 8,8 | 25 | 7,3 | 6,9 |
| 13 | 6,0 | 5,7 |
6.7. Групування даних
З математичної точки зору, при аналізі даних деяка кількість інформації повинна бути віднесена до кожного даного чи їх групи. Наприклад, до кількості клієнтів, яким надані послуги, відносять дату, день тижня, прізвище надавача послуг тощо.
Така дія називається групуванням даних. Таким чином, групування даних – це вибір з усієї сукупності однорідних даних за певною ознакою або згідно з визначеним принципом.
За допомогою групування намагаються створити умови, при яких отримані дані є більш однорідними і усувається вплив певних факторів.
Групування дозволяє визначити наявність кореляції там, де інакше вона не спостерігається. Приклади групованих та негрупованих даних показані на рис.30.

Рис.30. Груповані та негруповані дані.
Приклад. Для виявлення основних факторів, які впливають на якість наданих послуг в автосервісному виробництві, було проведене анкетне опитування головних спеціалістів підприємства ВАТ,, Автоцентр №1” [12]. В якості першого етапу із числа факторів були виділені чотири групи, які відрізняються за характером їх участі в процесі обслуговування:
1. Техніко – економічні;
2. Організаційні;
3. Економічні;
4. Соціально-економічні.
Залежність показника якості від факторів, які на нього впливають можна представити у вигляді:
y = f (x1,x2,x3,…,x18), де у – показник рівня якості продукції(рівня якості обслуговування автомобілів), визначається як відношення частки продукції вищої категорії якості до загального об’єму випуску, %;
х1,х2,…,х18 – фактори якості(табл. 13).
Таблиця 13.
Структура факторів, які впливають на рівень якості продукції підприємства.
| Технічні | Організаційні | Економічні | Соціальні |
| 1. Рівень автоматизації та механізації виробництва (х1),%. | 1. Коефіцієнт видачі автомобіля з першого разу (х9), %. | 1. Сума надбавки до зарплати за вищу категорію якості (х12),грн. | 1. Рівень підвищення кваліфікації працівників(х13),%. |
| 2. Питома вага прогресивних видів машин та обладнання (х2 ),%. | 2. Рівень спеціалізації виробництва (х10),%. | 2. Показник плинності кадрів (х14),%. | |
| 3. Питома вага використання прогресивних технологічних процесів (х3),%. | 3.Кількість отриманих рекламацій(х11), шт. | 3. Середній стаж роботи по даній спеціальності (х15), роки. | |
| 4. Коефіцієнт оновлення основних фондів (х4),%. | 4. Середній рівень освіти працівників(х16),роки. | ||
| 5. Рівень якості вихідних матеріалів, запчастин, комплектуючих (х5),%. | 5. Середній вік працівників(х17),роки. | ||
| 6. Ступінь зношеності обладнання (х6),%. | 6. Середній розмір місячної заробітної плати виробничого персоналу (х18),грн. | ||
| 7. Питома вага активної частини фондів (х7),%. | |||
| 8. Фондоозброєність одного працівника по активній частині основних фондів(х8),грн. |
Оскільки вибір факторів, які впливають на показник якості, являється в певній мірі довільним, тому завжди необхідно оцінити ступінь тісноти зв’язку між ними. Силу зв’язку між факторами та показником якості (в даному випадку: між технічними, соціальними, організаційними, економічними факторами та рівнем якості наданих послуг) можна визначити за допомогою коефіцієнта кореляції, який зручно обчилювати за формулою
 , (44)
, (44)
де  - відповідно середньоквадратичні відхилення величини x,y;
- відповідно середньоквадратичні відхилення величини x,y;
і = 1,2,…,n – кількість спостережень (значень) фактора х та ознаки у.
хі, уі – значення величини х, у для і – го вимірювання. Значення величин х1, х2,…, х18, у наведені в табл.14-15.
Таблиця 14.
Вибірка статистичних даних факторів, які впливають на якість роботи підприємства ВАТ,, Автоцентр №1”
| № | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 |
| 75,3 | 45,9 | 63,7 | 11,5 | 73,0 | 60,0 | 81,7 | 69,7 | 99,0 | 90,7 | 124,9 | 8,7 | |
| 75,1 | 43,7 | 64,9 | 9,9 | 72,9 | 59,0 | 81,0 | 69,6 | 98,0 | 90,4 | 124,7 | 7,8 | |
| 73,8 | 43,8 | 64,3 | 10,2 | 71,7 | 58,9 | 80,9 | 69,5 | 97,0 | 90,5 | 123,6 | 7,7 | |
| 74,2 | 43,2 | 63,8 | 10,0 | 71,8 | 58,8 | 80,0 | 69,4 | 96,0 | 90,6 | 123,4 | 6,7 | |
| 72,6 | 44,7 | 62,9 | 9,5 | 70,9 | 57,9 | 79,9 | 69,3 | 95,0 | 90,2 | 123,9 | 6,3 |
Продовження табл.14.
| № | X13 | X14 | X15 | X16 | X17 | X18 | y |
| 35,5 | 33,2 | 2,3 | 40,2 | ||||
| 35,7 | 33,1 | 2,4 | 39,9 | ||||
| 36,6 | 33,5 | 2,5 | 39,7 | ||||
| 36,7 | 33,3 | 2,6 | 39,8 | ||||
| 37,1 | 33,0 | 2,7 | 38,7 |
Таку ж таблицю даних можна отримати для інших підприємств системи автосервісу для кращого обґрунтування проблеми якості послуг та встановлення достовірних залежностей між статистичними показниками.
Таблиця 15.
Середні значення факторів(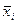 ) та параметра якості(
) та параметра якості( ) для підприємств системи автосервісу
) для підприємств системи автосервісу
| Фактор | Авто центр №1 | Авто центр №2 | Авто центр №3 | Авто центр №4 | Авто центр №5 | Авто центр №6 | Авто центр №7 | Авто центр №8 | Авто центр №9 | Авто центр №10 |
| X1 | 74,2 | |||||||||
| X2 | 44,26 | |||||||||
| X3 | 63,92 | |||||||||
| X4 | 10,22 | |||||||||
| X5 | 72,06 | |||||||||
| X6 | 58,92 | |||||||||
| X7 | 80,7 | |||||||||
| X8 | 69,5 | |||||||||
| X9 | ||||||||||
| X10 | 90,48 | |||||||||
| X11 | 124,1 | |||||||||
| X12 | 7,44 | 4,5 | 9,2 | 8,5 | ||||||
| X13 | 36,32 | |||||||||
| X14 | 33,22 | |||||||||
| X15 | 2,5 | 3,5 | 1,5 | 1,9 | 2,3 | |||||
| X16 | 57,2 | |||||||||
| X17 | 39,66 | |||||||||
| X18 | ||||||||||
| Y |
В результаті дослідження було встановлено який із факторів найбільше впливає на якість наданих послуг. Причому, крім даного підприємства, до уваги приймалися інші, які входять в систему підприємств фірмового обслуговування даної марки автомобіля. Встановили, що цими факторами виявилися: х5, х13. Саме цим проблемам необхідно приділити якомога більше уваги керівництву центрів системи автосервісу та відділів якості підприємств. Було виявлено, що приріст х5 на 1% призводить до збільшення рівня якості у на 0,56%.
Завдання для самостійної роботи. У відповідності до цього статистичного методу, проведіть розкладання(розшарування) даних за табл.13 -15; згрупуйте дані в залежності від умов їх отримання та проведіть обробку кожної групи даних окремо. Встановіть вид кореляції між фактором х13 та параметром якості у. Застосуйте всі принципи та інструменти управління якістю. Запропонуйте рекомендації щодо поліпшення якості роботи автосервісних підприємств.
ЛІТЕРАТУРА
1. Котлер Ф., Армстронг Г., Сондерс Д., Вонг В. Основы маркетинга / Пер. с англ.; 2-е европ.изд. – К.; М.; СПб.: Изд. дом. «Вильямс», 1998. –1056 с.
2. Shewhart W. Statistical Method from the Viewpoint of Quality Control. - N.Y.: Dover Publ., Inc., 1939 (reprint 1986). - 163 p.
3. ДСТУ ISO 9000-2001. Системи управління якістю. Основні положення та словник.
4. ДСТУ ISO 9001-2001. Системи управління якістю. Вимоги.
5. ДСТУ ISO 9004-2001. Системи управління якістю. Настанови щодо поліпшення діяльності.
6. Андрусенко С.І. Управління бізнес-процесами в організації. - Київ: НТУ, 2005. -78 с.
7. Сигорский В.П. Математический аппарат инженера / Издание 2-е, стереотипное. - К.: Техніка, 1977. -768 с.
8. Нив Г.Р. Пространство доктора Деминга. - М.: МГИЭТ (ТУ), 1996. - 344 с.
9. Juran J. La qualite dans les services. – Paris: Afnor gestion, 1987.
10. Захожай В.Б., Чорний А.Ю. Статистичне забезпечення управління якістю: Навчальний посібник. – К.: Центр навчальної літератури, 2005. – 340 с.
11. «Семь инструментов качества» в японской экономике. – М.: Издательство стандартов, 1990. – 88 с. (Серия «Качество, экономика, общество. Современные проблемы»).
12. Божок Г.П. Анализ, оценка и оптимизация системы менеджмента качества автосервисных региональных предприятий: Дис. … канд. техн. наук: 05.13.10. – Барнаул, 2003. – 210 с.
Поиск по сайту: