 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи линейного программирования
Рассмотрим этот метод применительно к задаче
 (1)
(1)
В данной задаче содержится пять переменных, поэтому целесообразно вначале решить двойственную задачу, а затем найдем решение исходной задачи.
Запишем исходную задачу в стандартной форме:
 (2)
(2)
Составим двойственную задачу:
 (3)
(3)
u 1 ³ 0, u 2 ³ 0. (4)
w = –5 u 1 + 6 u 2 ® min (5)
В двойственной задаче каждой неизвестной xj исходной задачи соответствует неравенство типа "³".
Найдем в двойственной задаче (3) оптимальное решение графическим способом.
Построим прежде всего в системе координат u 1 Ou 2 область допустимых решений (ОДР) задачи. Для этого, заменив каждое из неравенств (3) равенством, строим соответствующую граничную прямую ai 1 u 1 + ai 2 u 2 = ai 0 (i = 1, 2,…, r). Эта прямая делит плоскость u 1 Ou 2 на две полуплоскости (рис.1). Для координат u 1, u 2 любой точки А одной полуплоскости выполняется неравенство ai 1 u 1 + ai 2 u 2 £ ai 0, а для любой точки В другой полуплоскости – противоположное неравенство ai 1 u 1 + ai 2 u 2 ³ ai 0.
Координаты любой точки граничной прямой удовлетворяют уравнению ai 1 u 1 + ai 2 u 2 = ai 0.

Итак, имеем пять уравнений, определяющих пять граничных прямых:
– u 1 + 2 u 2 = 2 (1)
– u 2 = –3 (2)
2 u 1 – u 2 = 2 (3)
u 2 = 1 (4)
–2 u 2 = –10 (5)
u 1 = 0 (6)
u 2 = 0 (7)
На рис. 2 проведены все граничные прямые со стрелками, указывающими расположение искомых полуплоскостей, и показана ОДР с ее границей.
В этой области необходимо отыскать точку минимума целевой функции w = –5 u 1 + 6 u 2 двойственной задачи. Находим градиент функции w, он равен  = (–5, 6). Из начала координат в направлении к точке (–5, 6) проводим вектор произвольной длины – нормаль к линиям уровня линейной функции w. Перпендикулярно этому вектору проводится какая-нибудь прямая. Это и будет одна из линий уровня линейной функции. Ее уравнение будет –5 u 1 + 6 u 2 = h. На рис. 1 проведена линия нулевого уровня – прямая, проходящая через начало координат, ее уравнение имеет вид –5 u 1 + 6 u 2 = 0. Целевая функция w на всех точках этой прямой принимает нулевое значение. Если двигать эту прямую параллельно в направлении нормали, функция w будет возрастать. Ближайшая точка из ОДР, которой коснется линия уровня, и будет точкой минимума U *. В нашем примере этой точкой является точка А.
= (–5, 6). Из начала координат в направлении к точке (–5, 6) проводим вектор произвольной длины – нормаль к линиям уровня линейной функции w. Перпендикулярно этому вектору проводится какая-нибудь прямая. Это и будет одна из линий уровня линейной функции. Ее уравнение будет –5 u 1 + 6 u 2 = h. На рис. 1 проведена линия нулевого уровня – прямая, проходящая через начало координат, ее уравнение имеет вид –5 u 1 + 6 u 2 = 0. Целевая функция w на всех точках этой прямой принимает нулевое значение. Если двигать эту прямую параллельно в направлении нормали, функция w будет возрастать. Ближайшая точка из ОДР, которой коснется линия уровня, и будет точкой минимума U *. В нашем примере этой точкой является точка А.
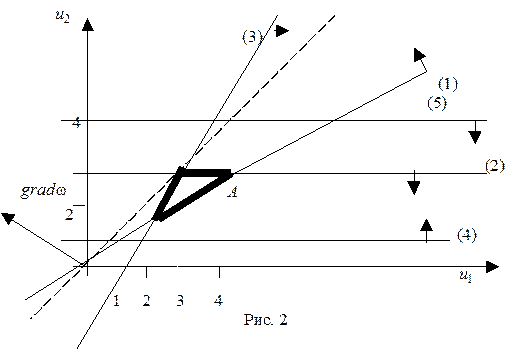
Найденная точка минимума находится на пересечении первой и второй граничных прямых, уравнения которых известны. Определим координаты этой точки аналитическим путем решения системы уравнений (1) и (2). Имеем систему

из которой получаем U * = (4, 3). Значение целевой функции на этом решении равно w* = –5 × 4 + 6 × 3 = –2.
Теперь определяем оптимальный план исходной задачи.
x 1 v 1 = 0, v 1 = – u 1 + 2 u 2 – 2 = –4 + 2 × 3 – 2 = 0 Þ x 1 > 0,
x 2 v 2 = 0, v 1 = – u 2 + 3 = –3 + 3 = 0 Þ x 2 > 0,
x 3 v 3 = 0, v 1 = 2 u 1 – u 2 – 2 = 2 × 4 – 3 – 2 = 2 Þ x 3 = 0,
x 4 v 4 = 0, v 4 = u 2 – 1 = 3 – 1 = 2 Þ x 4 = 0,
x 5 v 5 = 0, v 5 = –2 u 2 + 10 = –2 × 8 + 10 = 2 Þ x 5 = 0
Дальше определяем, какие неравенства исходной задачи на оптимальном решении X * обращаются в уравнения:
u 1 y 1 = 0, u 1 = 4 Þ y 1 = 0 ~ – x 1 +2 x 3 = –5,
u 2 y 2 = 0, u 2 = 3 Þ y 2 = 0 ~ 2 x 1 – x 2 – x 3 + x 4 – 2 x 5 = 6
Приходим к следующей системе уравнений:
– x 1 +2 x 3 = –5,
2 x 1 – x 2 – x 3 + x 4 – 2 x 5 = 6,
откуда X *(5, 4, 0, 0, 0). Значение целевой функции на этом плане равно
z * = 2 × 5 – 3 × 4 + 2 × 0 + 0 – 10 × 0 = –2.
Выпишем итоговые результаты решения задачи:
U * = (4, 3), X * = (5, 4, 0, 0, 0), z * = w* = –2
Симплекс-метод
Проиллюстрируем алгоритм симплекс-метода на решении простейшей задачи:
–2 x 1 + 2 x 2 – 2 x 3 + 2 x 4 £ 2,
2 x 1 + 2 x 2 + x 3 ³ 5,
– x 1 + x 2 – 2 x 3 + x 4 £ 0, (1)
x 1 – x 3 + 2 x 4 ³ –1,
x 1 ³ 0; x 2 ³ 0; x 3 ³ 0; x 4 ³ 0,

Подготовка задачи к решению
(составление начальной симплексной таблицы)
Формально начальная таблица составляется так: все коэффициенты стандартных неравенств записываются в начальную симплексную таблицу без изменения знаков, коэффициенты же нестандартных неравенств и максимизируемой функции меняют знаки на противоположные.
| – х 1 | – х 2 | – х 3 | – х 4 | ||
| y 1 = | –2 | –2 | |||
| y 2 = | –2 | –2 | –1 | –5 | |
| y 3 = | –1 | –2 | |||
| y 4 = | –1 | –2 | |||
| z = | –16 | –2 | –2 |
Умножая последовательно на верхнюю строку все остальные строки таблицы, получим исходную систему уравнений:







 (2)
(2)
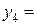



Система (2) используется в дальнейшем для контроля правильности определения неизвестных величин xj, yi и z.
Если составить двойственную задачу к исходной и перейти затем к эквивалентной канонической форме, то ее можно представить в табличной форме:
| v 1 = | v 2 = | v 3 = | v 4 = | w = | |
| u 1 | –2 | –2 | |||
| u 2 | –2 | –2 | –1 | –5 | |
| u 3 | –1 | –2 | |||
| u 4 | –1 | –2 | |||
| –2 | –2 |
Здесь ui – это двойственные переменные, соответствующие строчным неизвестным yi исходной задачи, vj – двойственные переменные, соответствующие столбцовым переменным xj, а w – целевая функция двойственной задачи.
Система двойственных уравнений получается последовательным умножением на левый столбец таблицы всех остальных ее столбцов:
 ,
,


 ,
,


 , (3)
, (3)
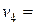

 ,
,


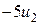 +
+ 
Система (3) используется в дальнейшем для проверки правильности значений двойственных переменных ui, vj и значения двойственной целевой функции w. Так как все числовые коэффициенты обеих таблиц совпадают, то они могут быть совмещены в единую таблицу следующего вида:
| v 1 = – x 1 | v 2 = – x 2 | v 3 = – x 3 | v 4 = – x 4 | w = | ||
| u 1 y 1 = | –2 | –2 | ||||
| u 2 y 2 = | –2 | –2 | –1 | –5 | ||
| u 3 y 3 = | –1 | –2 | ||||
| u 4 y 4 = | –1 | –2 | ← | |||
| z = | –2 | –2 | ||||
| ↑ |
На этом завершается этап построения начальной симплексной таблицы.
Поиск оптимального решения
Выпишем из нее начальное прямое и двойственное решения
X = (0, 0, 0, 0), Y = (2, –5, 0, 1), z = 0,
V = (16, –2, 8, –2), U = (0, 0, 0, 0), w = 0
Как видно, решение пары двойственных задач начинается с нулевых значений их основных неизвестных. Нулевой вектор X не является допустимым решением исходной задачи (1), т.к. он не удовлетворяет второму неравенству, о чем свидетельствует отрицательность второй компоненты вектора Y. Точно так же нулевой вектор U не является допустимым решением в двойственной задаче, так как вектор V содержит отрицательные компоненты.
Следовательно, задачу необходимо решать в два этапа.
Решение начинается с реализации процедуры поиска разрешающего столбца.
Вторая строка в последнем столбце содержит отрицательный элемент, т.к. первый, второй и третий столбцы содержат отрицательные элементы, то любой из них может быть разрешающим. Возьмем, например, в качестве разрешающего третий столбец. На этом выполнение первой процедуры заканчивается.
Процедура поиска разрешающей строки. Находим минимальное неотрицательное отношение элементов последнего столбца и разрешающего (третьего) столбцов,  = 1. Минимальное отношение соответствует четвертой строке, она и будет разрешающей (разрешающие строка и столбец показаны на таблице стрелками). Элемент 1, стоящий на пересечении разрешающего столбца и разрешающей строки, становится разрешающим.
= 1. Минимальное отношение соответствует четвертой строке, она и будет разрешающей (разрешающие строка и столбец показаны на таблице стрелками). Элемент 1, стоящий на пересечении разрешающего столбца и разрешающей строки, становится разрешающим.
Переходим к третьей процедуре – преобразованию симплексной таблицы относительно разрешающего элемента. Меняется «шапка» таблицы – пары переменных u 4 y 4 и v 3 x 3 меняются ролями и местами.
В результате преобразования получим следующую таблицу
| v 1 = – x 1 | v 2 = – x 2 | u 4 = – y 4 | v 4 = – x 4 | w = | ||
| u 1 y 1 = | –4 | –2 | ||||
| u 2 y 2 = | –3 | –2 | –2 | –4 | ||
| u 3 y 3 = | –3 | –3 | ||||
| v 3 x 3 = | –1 | –2 | ||||
| z = | –2 | –8 | –8 | |||
| |
Вычисление новых элементов таблицы лучше начинать с последних столбца и строки, т.к. в случае неотрицательности прямого и двойственного решений процесс отыскания решения заканчивается.
Разрешающий элемент 1 заменен на обратную величину  . Четвертая строка получена делением разрешающей строки на разрешающий элемент 1. Третий столбец получен делением разрешающего столбца на элемент, противоположный разрешающему, т.е. на –1.
. Четвертая строка получена делением разрешающей строки на разрешающий элемент 1. Третий столбец получен делением разрешающего столбца на элемент, противоположный разрешающему, т.е. на –1.
Все остальные элементы рассчитаны по правилу прямоугольника. Например, чтобы вычислить новый элемент второй строки и четвертого столбца, берется соответствующий этому элементу прямоугольник, откуда
новый элемент =  =
= 
Полученная таблица определяет следующие новые решения исходной и двойственной задач:
Х = (0, 0, 1, 0), Y = (4, -4, 2, 0), z = –8,
V = (24, –2, 0, 14), U = (0, 0, 0, -8), w = –8
Для контроля правильности найденных компонент прямого и двойственного решений необходимо подставить их в системы уравнений исходной (2) и двойственной задач (3).
Проверка решения
Прямого Двойственного
 4 = 2 ´ 0 – 2 ´ 0 + 2 ´ 1 – 2 ´ 0 + 2 24 = –2 ´ 0 – 2 ´ 0 – 0 – (–8) + 16
4 = 2 ´ 0 – 2 ´ 0 + 2 ´ 1 – 2 ´ 0 + 2 24 = –2 ´ 0 – 2 ´ 0 – 0 – (–8) + 16
–4 = 2 ´ 0 + 2 ´ 0 + 1 – 5 –2 = 2 ´ 0 – 2 ´ 0 + 0
2 = 0 – 0 + 2 ´ 1 – 0 0 = –2 ´ 0 – 0 – 2 ´ 0 – (–8) + 8
0 = 0 – 1 + 2 ´ 0 + 1 14 = 2 ´ 0 + 0 – 2 ´ (–8) – 2
–8 = –16 ´ 0 + 2 ´ 0 – 8 ´ 1 + 2 ´ 0 –8 = 2 ´ 0 – 5 ´ 0 – 8
Найденные решения удовлетворяют уравнениям исходной и двойственной задач. Получением новых решений и проверкой заканчивается одна итерация симплекс-метода.
Так как вектор Y по-прежнему содержит отрицательную компоненту y 2 = –4, то вектор X не является допустимым решением исходной задачи.
Переходим к выполнению второй итерации симплекс-метода.
Берем вторую строку табл.1 с отрицательным элементом в последнем столбце. В качестве разрешающего столбца возьмем второй столбец. Находим  . Минимальное отношение отвечает первой, второй и третьей строкам, поэтому в качестве разрешающей можно взять любую из них. Возьмем, например, вторую строку. Элемент –2, обведенный прямоугольником в таблице, будет разрешающим.
. Минимальное отношение отвечает первой, второй и третьей строкам, поэтому в качестве разрешающей можно взять любую из них. Возьмем, например, вторую строку. Элемент –2, обведенный прямоугольником в таблице, будет разрешающим.
В результате преобразования получим следующую таблицу.
| v 1 = – x 1 | u 2 = – y 2 | u 4 = – y 4 | v 4 = – x 4 | w = | ||
| u 1 y 1 = | –7 | –4 | ||||
| v 2 x 2 = | 3/2 | –1/2 | –1/2 | |||
| u 3 y 3 = | –3/2 | 1/2 | –5/2 | –4 | ||
| v 3 x 3 = | –1 | –2 | ||||
| z = | –1 | –9 | –4 | |||
| |
Таблица определяет новые решения прямой и двойственной задач.
X = (0, 2, 1, 0), Y = (0, 0, 0, 0), z = –4,
V = (27, 0, 0, 16), U = (0, -1, 0, -9), w = –4
Проверка решения
 Прямого Двойственного
Прямого Двойственного
 0 = 2 ´ 0 – 2 ´ 2 + 2 ´ 1 – 2 ´ 0 + 2 27 = –2 ´ 0 – 2 ´ (–1) – 0 – (–9) + 16
0 = 2 ´ 0 – 2 ´ 2 + 2 ´ 1 – 2 ´ 0 + 2 27 = –2 ´ 0 – 2 ´ (–1) – 0 – (–9) + 16
0 = 2 ´ 0 + 2 ´ 2 + 1 – 5 0 = 2 ´ 0 – 2 ´ (–1) + 0 – 2
0 = 0 – 2 + 2 ´ 1 – 0 0 = –2 ´ 0 – (–1) – 2 ´ 0 + (–9) + 8
0 = 0 – 1 + 2 ´ 0 + 1 16 = 2 ´ 0 + 0 – 2 ´ (–9) – 2
–4 = –16 ´ 0 + 2 ´ 2 – 8 ´ 1 + 2 ´ 0 –4 = 2 ´ 0 – 5 ´ (–1) + (–9)
Все компоненты векторов X и Y в (7) неотрицательны, следовательно, они определяют допустимое решение исходной задачи (1). На этом этап I завершается и осуществляется переход к этапу II – оптимизации полученного допустимого решения.
Проверяем план на оптимальность. Так как z -строка содержит отрицательные двойственные оценки u 2 = –1 и u 4 = –9, то полученное допустимое решение не оптимально и его следует попытаться улучшить.
Переходим к третьей итерации.
Среди отрицательных оценок z -строки выбирается какая-нибудь одна. В нашем примере имеются две отрицательных оценки. В качестве разрешающего столбца возьмем, например, третий столбец. Находим минимальное симплексное отношение  . Минимум соответствует первой строке, элемент 3 этой строки становится разрешающим. После преобразования получаем следующую таблицу:
. Минимум соответствует первой строке, элемент 3 этой строки становится разрешающим. После преобразования получаем следующую таблицу:
| v 1 = – x 1 | u 2 = – y 2 | u 1 = – y 1 | v 4 = – x 4 | w = | |
| u 4 y 4 = | –7/3 | 1/3 | 1/3 | –4/3 | |
| v 2 x 2 = | 1/6 | ||||
| u 3 y 3 = | 5/6 | ||||
| v 3 x 3 = | –1/3 | ||||
| z = | –4 |
Так как последние столбец и стока табл.3 неотрицательные, следовательно, прямое и двойственное решения оптимальны. Выпишем эти решения и проверим их. Имеем
X = (0, 2, 1, 0), Y = (0, 0, 0, 0), z = –4,
V = (6, 0, 0, 4), U = (3, 2, 0, 0), w = –4
Проверка решения
Прямого Двойственного
 0 = 2 ´ 0 – 2 ´ 2 + 2 ´ 1 – 2 ´ 0 + 2 6 = –2 ´ 3 – 2 ´ 2 – 0 – 0 + 16
0 = 2 ´ 0 – 2 ´ 2 + 2 ´ 1 – 2 ´ 0 + 2 6 = –2 ´ 3 – 2 ´ 2 – 0 – 0 + 16
0 = 2 ´ 0 + 2 ´ 2 + 1 – 5 0 = 2 ´ 3 – 2 ´ 2 + 0 – 2
0 = 0 – 2 + 2 ´ 1 – 0 0 = –2 ´ 3 – 2 – 2 ´ 0 + 0 + 8
0 = 0 – 1 + 2 ´ 0 + 1 4 = 2 ´ 3 + 0 – 2 ´ 0 – 2
–4 = –16 ´ 0 + 2 ´ 2 – 8 ´ 1 + 2 ´ 0 –4 = 2 ´ 3 – 5 ´ 2 + 0
Следовательно, оптимальное решение исходной задачи (1) задается вектором X * = (0, 2, 1, 0), оптимальные оценки ограничений вектором U * = (3, 2, 0, 0), при этом целевая функция принимает z * = w* = 4.
Транспортная задача
Рассмотрим алгоритм решения транспортной задачи на конкретном примере. Имеются четыре поставщика a 1 = 30, a 2 = 50, a 3 = 40, a 4 = 33, и имеются четыре потребителя b 1 = 58, b 2 = 22, b 3 = 18, b 4 = 22. Построить опорный план по правилу северо-западного угла, найти оптимальный план перевозки, обеспечивающий минимум суммарных затрат, если коэффициенты транспортных расходов на доставку груза от поставщиков к потребителям заданы матрицей 
В данной задаче четыре поставщика и четыре потребителя. Прежде чем приступить к решению транспортной задачи, необходимо ее закрыть, если она открытая.
Суммарный объем груза у поставщиков равен 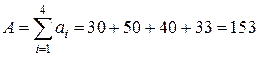 , а суммарная потребность составляет величину
, а суммарная потребность составляет величину  . Так как A > B, то задача открытая, и чтобы ее закрыть, вводим фиктивного потребителя с потребностью в грузе, равной разности A – B. Будем иметь
. Так как A > B, то задача открытая, и чтобы ее закрыть, вводим фиктивного потребителя с потребностью в грузе, равной разности A – B. Будем иметь  . Коэффициенты транспортных расходов на доставку груза от поставщиков к фиктивному потребителю полагаются равными нулю,
. Коэффициенты транспортных расходов на доставку груза от поставщиков к фиктивному потребителю полагаются равными нулю,  , i = 1, 2, 3, 4.
, i = 1, 2, 3, 4.
Составим закрытую транспортную задачу в табличной форме.
| bk | |||||||||
| ai | ||||||||||
| x 11 | x 12 | x 13 | x 14 | x 15 | ||||||
| x 21 | x 22 | x 23 | x 24 | x 25 | ||||||
| x 31 | x 32 | x 33 | x 34 | x 35 | ||||||
| x 41 | x 42 | x 43 | x 44 | x 45 |
Строки данной таблицы отвечают поставщикам, а столбцы потребителям.
Требуется найти оптимальный план поставок { xij }, i = 1,…,4; j = 1,…,5,т.е. такой план поставок, который:
1) сбалансирован с имеющимися запасами грузов у каждого поставщика и с заданными потребностями каждого потребителя;
2) имеет наименьшие транспортные расходы на доставку всех грузов по сравнению с другими планами поставок.
Поиск по сайту: