 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод потенциалов
Потенциалы  поставщиков и
поставщиков и  потребителей находятся из уравнений вида
потребителей находятся из уравнений вида  .
.
Для определенности примем, что  .
.

| bj | ui | |||||||||
| ai | |||||||||||
| – | + | ||||||||||
| + | – | ||||||||||
| + | – | ||||||||||
| + | – | ||||||||||
| vj |
Выбираем первую строку и полагаем  . В этой строке одна занятая клетка, расположенная в первом столбце. Следовательно, можно найти потенциал
. В этой строке одна занятая клетка, расположенная в первом столбце. Следовательно, можно найти потенциал  по формуле
по формуле  . Просматривая первый столбец, находим в нем занятую клетку (2, 1), неиспользованную еще для нахождения потенциалов. С ее помощью находим потенциал
. Просматривая первый столбец, находим в нем занятую клетку (2, 1), неиспользованную еще для нахождения потенциалов. С ее помощью находим потенциал 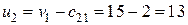 . С помощью
. С помощью  и клетки (2, 2) находим
и клетки (2, 2) находим  и т.д.
и т.д.
Проверка плана на оптимальность
Вычислим величины 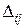 для свободных клеток. Имеем
для свободных клеток. Имеем


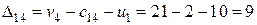



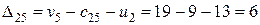




 .
.
Условие оптимальности нарушается для многих клеток, поэтому найденный план неоптимален.
Улучшение плана поставок
Среди положительных величин 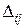 выбирается максимальная. В нашем случае величины
выбирается максимальная. В нашем случае величины  и
и  являются максимальными. Выбирается какая-нибудь одна из них, например, величина
являются максимальными. Выбирается какая-нибудь одна из них, например, величина  . Клетка (1, 5) помечается знаком «+» в левом верхнем углу.
. Клетка (1, 5) помечается знаком «+» в левом верхнем углу.
Смотрим, с какой занятой клеткой первой строки или пятого столбца можно соединить клетку (1, 5). Построим цикл, двигаясь от клетки (1, 5), например, по часовой стрелке.
В пятом столбце имеется единственная занятая клетка (4, 5), с которой можно соединить клетку (1, 5). Следующее звено ломаной должно находиться в четвертой строке. Так как в этой строке тоже единственная занятая клетка (4, 4), то ее следует соединить с клеткой (4, 5). Очередное звено ломаной должно находиться в четвертом столбце таблицы – это будет звено, соединяющее клетки (4, 4) и (3, 4).Следующее звено должно находиться в третьей строке, а в ней две занятые клетки. Для отыскания нужной клетки применяется метод проб и ошибок. Попробуем соединить клетки (3, 4) и (3, 3). Так как в одной строке таблицы не может быть более одного звена ломаной, то следующее звено должно быть расположено после такого соединения в третьем столбце таблицы. Однако в третьем столбце нет больше занятых клеток, поэтому таким путем нельзя замкнуть ломаную. Клетка (3, 3), следовательно, является тупиковой и ее не следует соединять с клеткой (3, 4). Остается единственная возможность – соединить клетку (3, 4) с занятой клеткой (3, 2). Далее процесс построения цикла пойдет однозначно.
Следующее звено должно находиться во втором столбце, поэтому соединяем клетки (3, 2) и (2, 2). Затем в цикл войдут клетки (2, 1) и (1, 1). Соединяя клетки (1, 1) и (1, 5), ломаная линия замыкается.
Начиная с клетки (1, 5) обойдем клетки цикла по часовой стрелке, отмечая их попеременно знаками плюс и минус.
В нашем примере четыре минусовых клетки в цикле – это клетки (4, 5), (3, 4), (2, 2) и (1, 1). Минимальная поставка находится в двух клетках: (2, 2) и (3, 4), т.е. 
Переходим к новому плану поставок

| bj | ui | |||||||||
| ai | |||||||||||
| – | + | ||||||||||
| + | – | ||||||||||
| + | – | ||||||||||
| vj |
Перейдем ко второй итерации. Проверяем план на оптимальность. Находим потенциалы, согласованные с полученным планом. Пусть  тогда
тогда


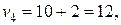
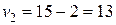 ,
, 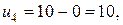



Считаем величины 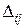 для свободных клеток.
для свободных клеток.
 ,
,  ,
,
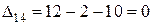 ,
, 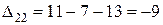 ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
, 
План не оптимален, так как среди величин D ij имеются положительные. Находим maxD ij = D31 = 7.
| bj | ui | ||||||||||
| ai | |||||||||||
| – | + | ||||||||||
| + | – | – | |||||||||
| + | – | ||||||||||
| vj |
Клетку (3, 1) отмечаем знаком плюс и находим цикл. Минимальная поставка в минусовых клетках цикла равна  Клетка (3, 1) при переходе к новой табл.5 занимается в данном случае нулевой поставкой, а клетка (3, 4), соответствующая минимальной поставке, освобождается. Так как
Клетка (3, 1) при переходе к новой табл.5 занимается в данном случае нулевой поставкой, а клетка (3, 4), соответствующая минимальной поставке, освобождается. Так как  , то новый план поставок совпадает со старым. Транспортные расходы по новому плану также останутся прежними, т.е.
, то новый план поставок совпадает со старым. Транспортные расходы по новому плану также останутся прежними, т.е.  Однако потенциалы изменятся.
Однако потенциалы изменятся.
Выполним третью итерацию. Вычислим потенциалы, полагая  Находим величины
Находим величины 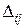 для свободных клеток табл.5.
для свободных клеток табл.5.

Так как maxD ij = D42 = 3 > 0, то план неоптимален. Отмечаем клетку (4, 2) знаком плюс и строим цикл, который в данном случае образуют клетки (4, 2), (3, 2), (3, 1), (1, 1), (1, 5) и (4, 5).
| bj | ui | |||||||||
| ai | |||||||||||
| vj |
Выполним четвертую итерацию. Находим новую систему потенциалов, согласованную с полученным планом, полагая  Проверяем план на оптимальность:
Проверяем план на оптимальность:

Все  Следовательно, получен оптимальный план. При этом
Следовательно, получен оптимальный план. При этом 

Теория игр
Проиллюстрируем решение матричной игры на конкретном примере, с заданной платежной матрицей  .
.
Составим следующую таблицу.

| j | a i | ||||
| i | ||||||
| –1 | –1 | |||||
| b j | 
| a = | ||||
| b = |
Имеем  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Так как  , поэтому седловой точки у данной матрицы нет, и следовательно, игра не имеет оптимального решения в чистых стратегиях.
, поэтому седловой точки у данной матрицы нет, и следовательно, игра не имеет оптимального решения в чистых стратегиях.
Найдем оптимальное решение матричной игры двумя способами: графически и путем сведения игры к задаче линейного программирования.
Графический способ решения матричной игры
Графически решаются задачи в случае, когда у одного из игроков всего лишь две чистые стратегии. В рассматриваемом примере у игрока I две стратегии, а у игрока II – четыре стратегии.
Графически решается задача игрока, имеющего две стратегии, т.е. в нашем случае задача игрока I. Оптимальная стратегия игрока II находится аналитическим путем после решения задачи игрока I.
На рисунке четыре отрезка, соответствующие четырем чистым стратегиям игрока II.
Находим теперь нижнюю границу выигрышей игрока I в виде ломаной линии, огибающей снизу все эти отрезки. Эта граница показана на рисунке жирной линией.

Решение задачи игрока I сводится к отысканию на нижней границе его выигрышей точки, соответствующей наибольшему выигрышу, т.е. наиболее удаленной точки отрезка.
На рисунке это будет точка М, находящаяся на пересечении первого и второго отрезков. Первая и вторая чистые стратегии игрока II называются активными, и он их должен использовать в своей оптимальной стратегии q * с ненулевой вероятностью. Третий и четвертый отрезки не проходят через точку М, поэтому третья и четвертая стратегии, наоборот, называются пассивными – игрок II не должен их использовать в оптимальной стратегии.
Далее определяются графически цена игры v как расстояние от точки М до единичного отрезка (взятое с учетом знака) и оптимальная смешанная стратегия  . Так как графическое определение числовых значений этих величин является довольно грубым, то следует уточнить их аналитическим путем решения системы линейных уравнений.
. Так как графическое определение числовых значений этих величин является довольно грубым, то следует уточнить их аналитическим путем решения системы линейных уравнений.



 1
1
Решив полученную систему, находим 


Найдем теперь оптимальную стратегию игрока II. Как уже отмечалось, третья и четвертая стратегии его являются пассивными, поэтому  Остальные компоненты вектора q * находятся аналитическим путем решения системы уравнений
Остальные компоненты вектора q * находятся аналитическим путем решения системы уравнений

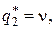

 +
+ 
Так как значение v уже известно, то для определения неизвестных достаточно взять какие-либо два уравнения этой системы. Возьмем, например, первое и третье уравнения:

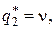
 +
+ 
откуда находим 

В итоге получены следующее оптимальное решение игры и ее цена:

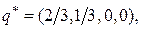

Замечание. При практическом составлении систем уравнений для нахождения оптимальных стратегий игроков использованы лишь два столбца матрицы А, соответствующие активным стратегиям игрока II, т.е. матрица 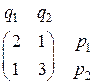
При составлении системы уравнений для игрока I столбцы этой матрицы умножаются скалярно на столбец неизвестных  , а при составлении системы для игрока II строчки этой матрицы скалярно умножаются на строку неизвестных (q 1, q 2).
, а при составлении системы для игрока II строчки этой матрицы скалярно умножаются на строку неизвестных (q 1, q 2).
Линейно-программный способ решения матричной игры
Необходимо решить линейно-программным способом игру с платежной матрицей  .
.
Добавим ко всем элементам матрицы А положительное число а= 1, получим матрицу  .
.
Тогда задачи I и II будут таковы:
 Задача I
Задача I
 Задача II
Задача II
Так как задача II имеет стандартную форму с положительным вектором ограничений, то для нее известен опорный план, и она может быть решена за один этап. Поэтому рекомендуется решать симплекс-методом задачу II, а решение задачи I получится как двойственное решение. Составляем начальную симплексную таблицу.
| v 1 = | v 2 = | v 3 = | v 4 = | w = | |
| – x 1 | – x 2 | – x 3 | – x 4 | ||
| u 1 y 1 = | |||||
| u 2 y 2 = | |||||
| z = | –1 | –1 | –1 | –1 |
Преобразуем таблицу относительно выбранного, по правилам симплекс-метода, разрешающего элемента, получим новую таблицу
| v 1 = | v 2 = | v 3 = | v 4 = | w = | |
| – x 1 | – x 2 | – x 3 | – x 4 | ||
| u 1 y 1 = | 1/3 | 2/3 | 6/3 | 5/3 | 1/3 |
| u 2 y 2 = | –2/3 | 8/3 | –12/3 | 5/3 | 1/3 |
| z = | 1/3 | –1/3 | 2/3 | 1/3 |






Решая задачу далее, получим
| v 1 = | v 2 = | v 3 = | v 4 = | w = | |
| – x 1 | – x 2 | – x 3 | – x 4 | ||
| u 1 y 1 = | 2/8 | ||||
| u 2 y 2 = | 1/8 | ||||
| z = | 2/8 | 1/8 | 1/2 | 7/3 | 3/8 |
Получены оптимальные решения задач I и II.
 ,
,  ,
, 
 ,
,  ,
,  .
.
Находим цену игры v и оптимальные стратегии игроков
 ,
,  .
.
 .
.
Цена игры v исходной игры равна  .
.
Составители:
Бабин Владислав Николаевич
Бильданов Ринат Талгатович
Грунина Мария Викторовна
Поиск по сайту: