 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лабораторная работа №2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
Цель работы: изучить законы вращательного и колебательного движений и освоить метод определения момента инерции тела.
Приборы и принадлежности: физический маятник, секундомер, измерительная линейка.
ТЕОРИЯ
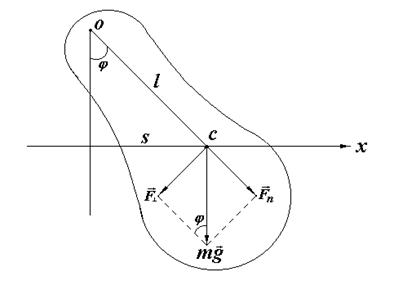
Физический маятник – твердое тело произвольной формы, произвольных размеров, способное колебаться относительно горизонтальной оси, не проходящей через центр масс (рис.1).
|
| Рис.1 |
О - точка, через которую проходит ось вращения;
С - центр масс;
l = ОС – приведённая длина маятника;
S – смещение центра масс от положения равновесия;
φ - угол отклонения маятника от положения равновесия.
При выведении из положения равновесия физический маятник колеблется относительно оси, проходящей через точку О.
При отклонении маятника от положения равновесия на угол  силу тяжести
силу тяжести  можно разложить на составляющие
можно разложить на составляющие  Сила
Сила  создает вращающий момент сил:
создает вращающий момент сил:  .
.
Знак «-» показывает, что сила направлена к положению равновесия (против смещения).
При малых углах отклонения траекторию движения точки можно считать прямой линией, совпадающей с осью абсцисс. Если угол  меньше
меньше  , то
, то 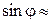
 , где
, где  берется в радианах.
берется в радианах.
Получим закон движения маятника. Из рисунка 1 видно, что  sin
sin 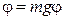 , тогда момент сил
, тогда момент сил
М = - mgl  . (1)
. (1)
Основной закон динамики вращательного движения можно записать в виде
М = I  , (2)
, (2)
где  угловое ускорение, I - момент инерции маятника.
угловое ускорение, I - момент инерции маятника.
Сравнивая (1) и (2), получим

или
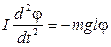 . (3)
. (3)
Разделив обе части выражения (3) на I, имеем
 . (4)
. (4)
Выражение (4) является дифференциальным уравнением движения физического маятника.
Произведя замену  , получим дифференциальное уравнение гармонического колебательного движения:
, получим дифференциальное уравнение гармонического колебательного движения:
 , где
, где  циклическая частота колебания.
циклическая частота колебания.
Она связана с периодом колебаний Т соотношением 
Тогда 
 отсюда
отсюда
 . (5)
. (5)
Зная период колебаний Т, можно рассчитать момент инерции I физического маятника.
Поиск по сайту: