Расчет ошибок прямого измерения

Пусть проведено n измерений некоторой величины Х. В результате получен ряд значений этой величины:

Наиболее вероятным является среднее арифметическое значение этой величины :

=

где i =1,2,3,…, n

Величина 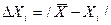называется абсолютной погрешностью отдельного измерения.

Средней арифметической погрешностью называют среднее арифметическое значение абсолютных погрешностей отдельных измерений:

Средняя арифметическая определяет интервал , внутри которого находится истинное значение измеряемой величины Х. Качество результата измерений характеризуется средней относительной погрешностью.

Средней относительной погрешностью называют отношение средней арифметической погрешности к среднему значению измеряемой величины :

Для более точного расчета абсолютной погрешности используют суммарную погрешность

Суммарная погрешность учитывает случайную погрешность , погрешность прибора , погрешность округления и определяется соотношением

, (1)

где определяют по формуле Стьюдента:

,

t - коэффициент Стьюдента (берется из таблицы Стьюдента), n - число измерений;

, где d - предельная ошибка прибора, указанная в паспорте.

, где - наименьшее деление прибора.

Поиск по сайту: