 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Информация
1,1,1, Понятие инсрорллаиии
Термин информация используется во многих науках и во многих сферах человеческой деятельности. Он происходит от латинского слова «шГогтаНо», что означает «сведения, разъяснения, изложение». Несмотря на привычность этого термина, строгого и общепринятого определения не существует. В рамках рассматриваемой нами науки «информация» является первичным и, следовательно, неопределимым понятием, подобно понятиям «точка» в математике, «тело» в механике, «поле» в физике. Несмотря на то, что этому понятию невозможно дать строгое определение, имеется возможность описать его через проявляемые свойства и мы попытаемся это сделать.
Как известно, в материальном мире все физические объекты, окружающие нас, являются либо телами, либо полями. Физические объекты, взаимодействуя друг с другом, порождают сигналы различных типов. В общем случае любой сигнал — это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики. Характеристика, которая используется для представления данных, называется параметром сигнала. Если параметр сигнала принимает ряд последовательных значений и их конечное число, то сигнал называется дискретным. Если параметр сигнала — непрерывная во времени функция, то сигнал называется непрерывным.
В свою очередь, сигналы могут порождать в физических телах изменения свойств. Это явление называется регистрацией сигналов. Сигналы, зарегистрированные на материальном носителе, называются данными. Существует большое количество физических методов регистрации сигналов на материальных носителях. Это могут быть механические воздействия, перемещения, изменения формы или магнитных, электрических, оптических параметров, химического состава, кристаллической структуры. В соответствии с методами регистрации, данные могут храниться и транспортироваться на различных носителях. Наиболее часто используемый и привычный носитель — бумага; сигналы регистрируются путем изменения ее оптических свойств. Сигналы могут быть зарегистрированы и путем изменения
магнитных свойств полимерной ленты с нанесенным ферромагнитным покрытием, как это делается в магнитофонных записях, и путем изменения химических свойств в фотографии.
Данные несут информацию о событии, но не являются самой информацией, так как одни и те же данные могут восприниматься (отображаться или еще говорят интерпретироваться) в сознании разных людей совершенно по-разному. Например, текст, написанный на русском языке (т.е. данные), даст различную информацию человеку, знающему алфавит и язык, и человеку, не знающему их.
Чтобы получить информацию, имея данные, необходимо к ним применить методы, которые преобразуют данные в понятия, воспринимаемые человеческим сознанием. Методы, в свою очередь, тоже различны. Например, человек, знающий русский язык, применяет адекватный метод, читая русский текст. Соответственно, человек, не знающий русского языка и алфавита, применяет неадекватный метод, пытаясь понять русский текст. Таком образом, можно считать, что информация — это продукт взаимодействия данных и адекватных методов.
Из вышесказанного следует, что информация не является статическим объектом, она появляется и существует в момент слияния методов и данных, все прочее время она находится в форме данных. Момент слияния данных и методов называется информационным процессом (рис. 1.1).

Рис. 1.1. Формирование информации
Человек воспринимает первичные данные различными органами чувств (их у нас пять — зрение, слух, осязание, обоняние, вкус), и на их основе сознанием могут быть построены вторичные абстрактные (смысловые, семантические) данные.
Таким образом, первичная информация может существовать в виде
рисунков, фотографий, звуковых, вкусовых ощущений, запахов, а вторичная — в виде чисел, символов, текстов, чертежей, радиоволн, магнитных записей.
1,1,2, СВойстВа инсрормаиии
Понятие «информация», как уже было сказано ранее, используется многими научными дисциплинами, имеет большое количество разнообразных свойств, но каждая дисциплина обращает внимание на те свойства информации, которые ей наиболее важны. В рамках нашего рассмотрения наиболее важными являются такие свойства, как дуализм, полнота, достоверность, адекватность, доступность, актуальность. Рассмотрим их подробнее.
Дуализм информации характеризует ее двойственность. С одной стороны, информация объективна в силу объективности данных, с другой — субъективна, в силу субъективности применяемых методов. Иными словами, методы могут вносить в большей или меньшей степени субъективный фактор и таким образом влиять на информацию в целом. Например, два человека читают одну и ту же книгу и получают подчас весьма разную информацию, хотя прочитанный текст, т.е. данные, были одинаковы. Более объективная информация применяет методы с меньшим субъективным элементом.
Полнота информации характеризует степень достаточности данных для принятия решения или создания новых данных на основе имеющихся. Неполный набор данных оставляет большую долю неопределенности, т.е. большое число вариантов выбора, а это потребует применения дополнительных методов, например, экспертных оценок, бросание жребия и т.п. Избыточный набор данных затрудняет доступ к нужным данным, создает повышенный информационный шум, что также вызывает необходимость дополнительных методов, например, фильтрацию, сортировку. И неполный и избыточный наборы затрудняют получение информации и принятие адекватного решения.
Достоверность информации — это свойство, характеризующее степень соответствия информации реальному объекту с необходимой точностью. При работе с неполным набором данных достоверность
информации может характеризоваться вероятностью, например, можно сказать, что при бросании монеты с вероятностью 50 % выпадет герб.
Адекватность информации выражает степень соответствия создаваемого с помощью информации образа реальному объекту, процессу, явлению. Полная адекватность достигается редко, так как обычно приходится работать с не самым полным набором данных, т.е. присутствует неопределенность, затрудняющая принятие адекватного решения. Получение адекватной информации также затрудняется при недоступности адекватных методов.
Доступность информации — это возможность получения информации при необходимости. Доступность складывается из двух составляющих: из доступности данных и доступности методов. Отсутствие хотя бы одного дает неадекватную информацию.
Актуальность информации. Информация существует во времени, так как существуют во времени все информационные процессы. Информация, актуальная сегодня, может стать совершенно ненужной по истечении некоторого времени. Например, программа телепередач на нынешнюю неделю будет неактуальна для многих телезрителей на следующей неделе.
1,1,3, Понятие количество инсрормоиии
Свойство полноты информации негласно предполагает, что имеется возможность измерять количество информации. Какое количество информации содержится в данной книге, какое количество информации в популярной песенке? Что содержит больше информации: роман «Война и мир» или сообщение, полученное в письме от товарища? Ответы на подобные вопросы не просты и не однозначны, так как во всякой информации присутствует субъективная компонента. А возможно ли вообще объективно измерить количество информации? Важнейшим результатом теории информации является вывод о том, что в определенных, весьма широких условиях, можно, пренебрегая качественными особенностями информации, выразить ее количество числом, а следовательно, сравнивать количество информации, содержащейся в различных группах данных.
Количеством информации называют числовую характеристику информации, отражающую ту степень неопределенности, которая исчезает после получения информации.
Рассмотрим пример: дома осенним утром, старушка предположила, что могут быть осадки, а могут и не быть, а если будут, то в форме снега или в форме дождя, т.е. «бабушка надвое сказала — то ли будет, то ли нет, то ли дождик, то ли снег». Затем, выглянув в окно, увидела пасмурное небо и с большой вероятностью предположила — осадки будут, т.е., получив информацию, снизила количество вариантов выбора. Далее, взглянув на наружный термометр, она увидела, что температура отрицательная, значит, осадки следует ожидать в виде снега. Таким образом, получив последние данные о температуре, бабушка получила полную информацию о предстоящей погоде и исключила все, кроме одного, варианты выбора.
Приведенный пример показывает, что понятия «информация», «неопределенность», «возможность выбора» тесно связаны. Получаемая информация уменьшает число возможных вариантов выбора (т.е. неопределенность), а полная информация не оставляет вариантов вообще.
За единицу информации принимается один бит (англ. Ы1 — Ыпагу йщИ — двоичная цифра). Это количество информации, при котором неопределенность, т.е. количество вариантов выбора, уменьшается вдвое или, другими словами, это ответ на вопрос, требующий односложного разрешения — да или нет.
Бит — слишком мелкая единица измерения информации. На практике чаще применяются более крупные единицы, например, байт, являющийся последовательностью из восьми бит. Именно восемь битов, или один байт, используется для того, чтобы закодировать символы алфавита, клавиши клавиатуры компьютера. Один байт также является минимальной единицей адресуемой памяти компьютера, т.е. обратиться в память можно к байту, а не биту.
Широко используются еще более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт = 210 байт, 1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт, 1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт, 1 Терабайт (Тбайт) - 1024 Гбайт = 240 байт.
За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации. Но данная единица используется редко в компьютерной технике, что связано с аппаратными особенностями компьютеров.
1,1,4, информационные проиессы
Получение информации тесно связано с информационными процессами, поэтому имеет смысл рассмотреть отдельно их виды.
Сбор данных — это деятельность субъекта по накоплению данных с целью обеспечения достаточной полноты. Соединяясь с адекватными методами, данные рождают информацию, способную помочь в принятии решения. Например, интересуясь ценой товара, его потребительскими свойствами, мы собираем информацию для того, чтобы принять решение: покупать или не покупать его.
Передача данных — это процесс обмена данными. Предполагается, что существует источник информации, канал связи, приемник информации, и между ними приняты соглашения о порядке обмена данными, эти соглашения называются протоколами обмена. Например, в обычной беседе между двумя людьми негласно принимается соглашение, не перебивать друг друга во время разговора.
Хранение данных — это поддержание данных в форме, постоянно готовой к выдаче их потребителю. Одни и те же данные могут быть востребованы не однажды, поэтому разрабатывается способ их хранения (обычно на материальных носителях) и методы доступа к ним по запросу потребителя.
Обработка данных — это процесс преобразования информации от исходной ее формы до определенного результата. Сбор, накопление, хранение информации часто не являются конечной целью информационного процесса. Чаще всего первичные данные привлекаются для решения какой-либо проблемы, затем они преобразуются шаг за шагом в соответствии с алгоритмом решения задачи до получения выходных данных, которые после анализа пользователем предоставляют необходимую информацию.
1,1,5. инсрорллаиия В жизни челоВечестВа
Как мы уже выяснили, человечество со дня своего выделения из животного мира значительную часть своего времени и внимания уделяло информационным процессам.
На первых этапах носителем данных была память, и информация от одного человека к другому передавалась устно. Этот способ передачи информации был ненадежен и подвержен большим искажениям, ввиду естественного свойства памяти утрачивать редко используемые данные.
По мере развития цивилизации, объемы информации, которые необходимо было накапливать и передавать, росли, и человеческой памяти стало не хватать — появилась письменность. Это великое изобретение было сделано шумерами около шести тысяч лет назад. Оно позволило наряду с простыми записями счетов, векселей, рецептов записывать наблюдения за звездным небом, за погодой, за природой. Изменился смысл информационных сообщений. Появилась возможность обобщать, сопоставлять, переосмысливать ранее сохраненные сведения. Это же в свою очередь дало толчок развитию истории, литературы, точным наукам и в конечном итоге изменило общественную жизнь. Изобретение письменности характеризует первую информационную революцию.
Дальнейшее накопление человечеством информации привело к увеличению числа людей, пользовавшихся ею, но письменные труды одного человека могли быть достоянием небольшого окружения. Возникшее противоречие было разрешено созданием печатного станка. Эта веха в истории цивилизации характеризуется как вторая информационная революция (началась в XVI в.). Доступ к информации перестал быть делом отдельных лиц, появилась возможность многократно увеличить объем обмена информацией, что привело к большим изменениям в науке, культуре и общественной жизни.
Третья информационная революция связывается с открытием электричества и появлением (в конце XIX в.) на его основе новых средств коммуникации — телефона, телеграфа, радио. Возможности накопления информации для тех времен стали поистине безграничными, а скорость обмена очень высокой.
К середине XX в. появились быстрые технологические процессы, управлять которыми человек не успевал. Проблема управления
техническими объектами могла решаться только с помощью универсальных автоматов, собирающих, обрабатывающих данные и выдающих решение в форме управляющих команд. Ныне эти автоматы называются компьютерами. Бурно развивавшаяся наука и промышленность привели к росту информационных ресурсов в геометрической прогрессии, что породило проблемы доступа к большим объемам информации.
Наше время отмечается как четвертая информационная революция. Пользователями информации стали миллионы людей. Появились дешевые компьютеры, доступные миллионам пользователей. Компьютеры стали мультимедийными, т.е. они обрабатывают различные виды информации: звуковую, графическую, видео и др. Это, в свою очередь, дало толчок к широчайшему использованию компьютеров в различных областях науки, техники, производства, быта. Средства связи получили повсеместное распространение, а компьютеры для совместного участия в информационном процессе соединяются в компьютерные сети. Появилась всемирная компьютерная сеть Интернет, услугами которой пользуется значительная часть населения планеты, оперативно получая и обмениваясь данными, т.е. формируется единое мировое информационное пространство.
В настоящее время круг людей, занимающихся обработкой информации, вырос до небывалых размеров, а скорость обмена стала просто фантастической, компьютеры применяются практически во всех областях жизни людей.
На наших глазах появляется информационное общество, где акцент внимания и значимости смещается с традиционных видов ресурсов (материальные, финансовые, энергетические и пр.) на информационный ресурс, который, хотя всегда существовал, но не рассматривался ни как экономическая, ни как иная категория.
Информационные ресурсы — это отдельные документы и массивы документов в библиотеках, архивах, фондах, банках данных, информационных системах и других хранилищах. Иными словами, информационные ресурсы — это знания, подготовленные людьми для социального использования в обществе и зафиксированные на материальных носителях. Информационные ресурсы страны, региона, организации все чаще рассматриваются как стратегические ресурсы, аналогичные по значимости запасам сырья, энергии, ископаемых и прочим ресурсам.
Развитие мировых информационных ресурсов позволило:
• превратить деятельность по оказанию информационных услуг в
глобальную человеческую деятельность;
• сформировать мировой и внутригосударственный рынок инфор
мационных услуг;
• повысить обоснованность и оперативность принимаемых реше
ний в фирмах, банках, биржах, промышленности, торговле и др.
за счет своевременного использования необходимой информа
ции.
1.2. ЛреЭмет и структура информатики
Термин информатика получил распространение с середины 80-х гг. прошлого века. Он состоит из корня тГогт — «информация» и суффикса таИс8 — «наука о...». Таким образом, информатика — это наука об информации. В англоязычных странах термин не прижился, информатика там называется Сотри1ег 8с1епсе — наука о компьютерах.
Информатика — молодая, быстро развивающаяся наука, поэтому строгого и точного определения ее предмета пока не сформулировано. В одних источниках информатика определяется как наука, изучающая алгоритмы, т.е. процедуры, позволяющие за конечное число шагов преобразовать исходные данные в конечный результат, в других — на первый план выставляется изучение компьютерных технологий. Наиболее устоявшимися посылками в определении предмета информатики в настоящее время являются указания на изучение информационных процессов (т.е. сбора, хранения, обработки, передачи данных) с применением компьютерных технологий. При таком подходе наиболее точным, по нашему мнению, является следующее определение:
Информатика — это наука, изучающая:
• методы реализации информационных процессов средствами вычис
лительной техники (СВТ);
• состав, структуру, общие принципы функционирования СЕТ;
• принципы управления СВТ.
Из определения следует, что информатика — прикладная наука, использующая научные достижения многих наук. Кроме того, информатика - практическая наука, которая не только занимается описа-
тельным изучением перечисленных вопросов, но и во многих случаях предлагает способы их решения. В этом смысле информатика технологична и часто смыкается с информационными технологиями.
Методы реализации информационных процессов находятся на стыке информатики с теорией информации, статистикой, теорией кодирования, математической логикой, документоведением и т.д. В этом разделе изучаются вопросы:
• представление различных типов данных (числа, символы, текст,
звук, графика, видео и т.д.) в виде, удобном для обработки СВТ
(кодирование данных);
• форматы представления данных (предполагается, что одни и те
же данные могут быть представлены разными способами);
• теоретические проблемы сжатия данных;
• структуры данных, т.е. способы хранения с целью удобного дос
тупа к данным.
В изучении состава, структуры, принципов функционирования средств вычислительной техники используются научные положения из электроники, автоматики, кибернетики. В целом этот раздел информатики известен как аппаратное обеспечение (АО) информационных процессов. В этом разделе изучаются:
• основы построения элементов цифровых устройств;
• основные принципы функционирования цифровых вычисли
тельных устройств;
• архитектура СВ1 — основные принципы функционирования
систем, предназначенных для автоматической обработки данных;
• приборы и аппараты, составляющие аппаратную конфигурацию
вычислительных систем;
• приборы и аппараты, составляющие аппаратную конфигурацию
компьютерных сетей.
В разработке методов управления средствами вычислительной техники (а средствами цифровой вычислительной техники управляют программы, указывающие последовательность действий, которые должно выполнить СВТ) используют научные положения из теории алгоритмов, логики, теории графов, лингвистики, теории игр. Этот раздел информатики известен как программное обеспечение (ПО) СВТ. В этом разделе изучаются:
• средства взаимодействия аппаратного и программного обеспече
ния;
• средства взаимодействия человека с аппаратным и программным
обеспечением, объединяемые понятием интерфейс,
• программное обеспечение СВТ (ПО).
Обобщая сказанное, можно предложить следующую структурную схему (рис. 1.2):

Рис. 1.2. Структура информатики
В настоящей главе будут подробно рассмотрены некоторые проблемы представления данных различных типов: числовых, символьных, звуковых, графических. Также будут рассмотрены некоторые структуры, позволяющие хранить данные с возможностью удобного доступа к ним.
Вторая глава посвящена аппаратному обеспечению информационных процессов. В ней рассматриваются вопросы синтеза цифро-
вых устройств, устройство электронно-вычислительных машин, устройство отдельных элементов аппаратного обеспечения.
Третья составляющая информатики — программное обеспечение — неоднородна и имеет сложную структуру, включающую несколько уровней: системный, служебный, инструментальный, прикладной.
На низшем уровне находятся комплексы программ, осуществляющих интерфейсные функции (посреднические между человеком и компьютером, аппаратным и программным обеспечением, между одновременно работающими программами), т.е. распределения различных ресурсов компьютера. Программы этого уровня называются системными. Любые пользовательские программы запускаются под управлением комплексов программ, называемых операционными системами.
Следующий уровень — это служебное программное обеспечение. Программы этого уровня называются утилитами, выполняют различные вспомогательные функции. Это могут быть диагностические программы, используемые при обслуживании различных устройств (гибкого и жесткого диска), тестовые программы, представляющие комплекс программ технического обслуживания, архиваторы, антивирусы и т.п. Служебные программы, как правило, работают под управлением операционной системы (хотя могут и непосредственно обращаться к аппаратному обеспечению), поэтому они рассматриваются как более высокий уровень. В некоторых классификациях системный и служебный уровни объединяются в один класс — системного программного обеспечения (см. главу 3).
Инструментальное программное обеспечение представляет комплексы программ для создания других программ. Процесс создания новых программ на языке машинных команд очень сложен и кропотлив, поэтому он низкопроизводителен. На практике большинство программ составляется на формальных языках программирования, которые более близки к математическому, следовательно, проще и производительней в работе, а перевод программ на язык машинных кодов осуществляет компьютер посредством инструментального программного обеспечения. Программы инструментального программного обеспечения управляются системными программами, поэтому они относятся к более высокому уровню.
Прикладное программное обеспечение — самый большой по объему класс программ, это программы конечного пользователя. В чет-
вертой главе будет дано подробное описание и классификация программ, входящих в этот класс. Пока же скажем, что в мире существует около шести тысяч различных профессий, тысячи различных увлечений и большинство из них в настоящее время имеет какие-либо свои прикладные программные продукты. Прикладное программное обеспечение также управляется системными программами, и имеет более высокий уровень.
Обобщая сказанное, можно предложить следующую структуру программного обеспечения (рис. 1.3).

Рис. 1.3. Классификация программного обеспечения
Предложенная классификация программного обеспечения является в большой мере условной, так как в настоящее время программ-
ные продукты многих фирм стали объединять в себе программные элементы из разных классов. Например, операционная система \Мпёо\У8, являясь комплексом системных программ, в своем составе содержит блок служебных программ (дефрагментация, проверка, очистка диска и др.), а также текстовый процессор \УогёРас1, графический редактор Рат1, которые принадлежат классу прикладных программ.
1,3. Представление (кодирование) Эаннын
Чтобы работать с данными различных видов, необходимо унифицировать форму их представления, а это можно сделать с помощью кодирования. Кодированием мы занимаемся довольно часто, например, человек мыслит весьма расплывчатыми понятиями, и, чтобы донести мысль от одного человека к другому, применяется язык. Язык — это система кодирования понятий. Чтобы записать слова языка, применяется опять же кодирование — азбука. Проблемами универсального кодирования занимаются различные области науки, техники, культуры. Вспомним, что чертежи, ноты, математические выкладки являются тоже некоторым кодированием различных информационных объектов. Аналогично, универсальная система кодирования требуется для того, чтобы большое количество различных видов информации можно было бы обработать на компьютере.
Подготовка данных для обработки на компьютере (представление данных) в информатике имеет свою специфику, связанную с электроникой. Например, мы хотим проводить расчеты на компьютере. При этом нам придется закодировать цифры, которыми записаны числа. На первый взгляд, представляется вполне естественным кодировать цифру ноль состоянием электронной схемы, где напряжение на некотором элементе будет равно 0 вольт, цифру единица — 1 вольт, двойку — 2 вольт и т.д., девятку — 9 вольт. Для записи каждого разряда числа в этом случае потребуется элемент электронной схемы, имеющий десять состояний. Однако элементная база электронных схем имеет разброс параметров, что может привести к появлению напряжения, скажем, 3,5 вольт, а оно может быть истолкова-
но и как тройка и как четверка, т.е. потребуется на уровне электронных схем «объяснить» компьютеру, где заканчивается тройка, а где начинается четверка. Кроме того, придется создавать весьма непростые электронные элементы для производства арифметических операций с числами, т.е. на схемном уровне должны быть созданы таблица умножения — 10 х 10 = 100 схем и таблица сложения — тоже 100 схем. Для электроники 40-х гг. (время, когда появились первые вычислительные машины) это была непосильная задача. Еще сложнее выглядела бы задача обработки текстов, ведь русский алфавит содержит 33 буквы. Очевидно, такой путь построения вычислительных систем не состоятелен.
В то же время весьма просто реализовались электронные схемы с двумя устойчивыми состояниями: есть ток — 1, нет тока — О, есть электрическое (магнитное) поле — 1, нет — 0. Взгляды создателей вычислительной техники были обращены на двоичное кодирование как универсальную форму представления данных для дальнейшей обработки их средствами вычислительной техники. Предполагается, что данные располагаются в некоторых ячейках, представляющих упорядоченную совокупность из двоичных разрядов, а каждый разряд может временно содержать одно из состояний — 0 или 1. Тогда группой из двух двоичных разрядов (двух бит) можно закодировать 22 = 4 различные комбинации кодов (00, 01, 10, 11); аналогично, три бита дадут 23 = 8 комбинаций, восемь бит или 1 байт — 28 = 256 и т.д.
Итак, внутренняя азбука компьютера очень бедна, содержит всего два символа: О, 1, поэтому и возникает проблема представления всего многообразия типов данных — чисел, текстов, звуков, графических изображений, видео и др. — только этими двумя символами, с целью дальнейшей обработки средствами вычислительной техники. Вопросы представления некоторых типов данных мы рассмотрим в последующих параграфах.
1.3.1, Представление чисел В ЗВоичном коЗе
Существуют различные способы записи чисел, например: можно записать число в виде текста — сто двадцать три; римской системе счисления — СХХ1П; арабской — 123.
Системы счисления
Совокупность приемов записи и наименования чисел называется системой счисления.
Числа записываются с помощью символов, и по количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская. Например, для записи числа один используется буква I, два и три выглядят как совокупности символов II, III, но для записи числа пять выбирается новый символ V, шесть — VI, десять — вводится символ X, сто — С, тысяча — Ми т.д. Бесконечный ряд чисел потребует бесконечного числа символов для записи чисел. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.
Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим ^.
В повседневной жизни мы пользуемся десятичной позиционной системой счисления, я = 10, т.е. используется 10 цифр: 0123456 789.
Рассмотрим правила записи чисел в позиционной десятичной системе счисления. Числа от 0 до 9 записываются цифрами, для записи следующего числа цифры не существует, поэтому вместо 9 пишут 0, но левее нуля образуется еще один разряд, называемый старшим, где записывается (прибавляется) 1, в результате получается 10. Затем пойдут числа 11, 12, но на 19 опять младший разряд заполнится и мы его снова заменим на 0, а старший разряд увеличим на 1, получим 20. Далее по аналогии 30, 40... 90, 91, 92... до 99. Здесь заполненными оказываются два разряда сразу; чтобы получить следующее число, мы заменяем оба на 0, а в старшем разряде, теперь уже третьем, поставим 1 (т.е. получим число 100) и т.д. Очевидно, что, используя конечное число цифр, можно записать любое сколь угод-
но большое число. Заметим также, что производство арифметических действий в десятичной системе счисления весьма просто.
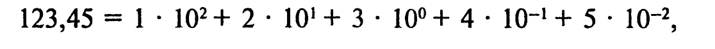
|
| а в общем виде это правило запишется так: |

|
Число в позиционной системе счисления с основанием ^ может быть представлено в виде полинома по степеням ц. Например, в десятичной системе мы имеем число
Здесь Х(ч) — запись числа в системе счисления с основанием я; х. — натуральные числа меньше я, т.е. цифры; п — число разрядов целой части; т — число разрядов дробной части.
Записывая слева направо цифры числа, мы получим закодированную запись числа в я-ичной системе счисления:

В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, я = 2. На ранних этапах развития вычислительной техники арифметические операции с действительными числами производились в двоичной системе ввиду простоты их реализации в электронных схемах вычислительных машин. Например, таблица сложения и таблица умножения будут иметь по четыре правила:

А значит, для реализации поразрядной арифметики в компьютере потребуются вместо двух таблиц по сто правил в десятичной системе счисления две таблицы по четыре правила в двоичной. Соответственно на аппаратном уровне вместо двухсот электронных схем — восемь.
Но запись числа в двоичной системе счисления длиннее записи
того же числа в десятичной системе счисления в 1о§2 10 раз (примерно в 3,3 раза). Это громоздко и не удобно для использования, так как обычно человек может одновременно воспринять не более пяти-семи единиц информации, т.е. удобно будет пользоваться такими системами счисления, в которых наиболее часто используемые числа (от единиц до тысяч) записывались бы одной-четырьмя цифрами. Как это будет показано далее, перевод числа, записанного в двоичной системе счисления, в восьмеричную и шестнадцатеричную очень сильно упрощается по сравнению с переводом из десятичной в двоичную. Запись же чисел в них в три раза короче для восьмеричной и в четыре для шестнадцатеричной системы, чем в двоичной, но длины чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления будут различаться ненамного. Поэтому, наряду с двоичной системой счисления, в информатике имеют хождение восьмеричная и шестнадцатеричная системы счисления.
Восьмеричная система счисления имеет восемь цифр: 01234 567. Шестнадцатеричная — шестнадцать, причем первые 10 цифр совпадают по написанию с цифрами десятичной системы счисления, а для обозначения оставшихся шести цифр применяются большие латинские буквы, т.е. для шестнадцатеричной системы счисления получим набор цифр: 0123456789АВСОЕЕ
Если из контекста не ясно, к какой системе счисления относится запись, то основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:
231<10)= 11100111(2)=347(8)=Е7(16).
Запишем начало натурального ряда в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.

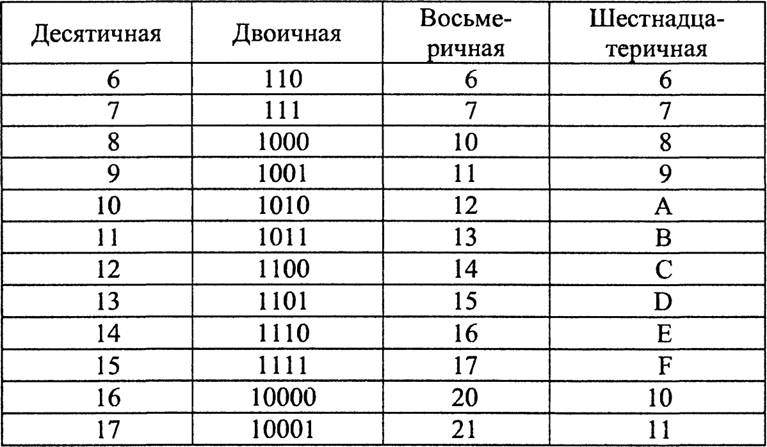
Преобразование чисел из оЗной системы счисление В Зругую
Так как десятичная система для нас удобна и привычна, все арифметические действия мы делаем в ней, и преобразование чисел из произвольной недесятичной (я *10) системы в десятичную удобно выполнять на основе разложения по степеням ц, например:
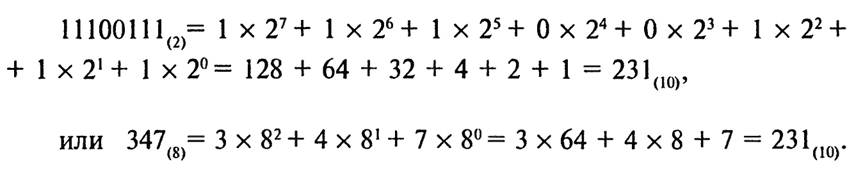
Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.
Рассмотрим алгоритм на примере перевода десятичного числа 231 в двоичную систему (совершенно аналогичен перевод из десятичной системы в любую я-ичную). Разделим число на два (основание системы): нацело 231: 2 = 115 и остаток 1, т.е. можно записать 231 = 115x2'+ 1 х 2°.
Число 115 (такой двоичной цифры нет) тоже может быть раз-
делено нацело на 2, т.е. 115: 2 = 57 и остаток 1. По аналогии запишем
231 = (57 х 2 + 1) х 2 + 1 = 57 х 22 4- 1 х I1 + 1 х 2°;
аналогично продолжим процесс дальше:
57: 2 = 28, остаток 1; 231 = ((28 х2+1)х2+1)х2+1 = 28х х 23 + 1 х 22 + 1 х 21 + 1 х 2°.
28: 2 = 14, остаток 0; 231 = (((14 х 2 + 0) х 2 +1) х 2 + 1) х 2 + + 1 = 14 х 24 + 1 х 22 + 1 х 21 + 1 х 2°.
14: 2 = 7, остаток 0; 231=((((7 х 2 + 0) х 2 + 0) х 2 + 1) х 2 + 1)х х2+ 1 = 7х25 + 1 х22+ 1 х2' + 1 х 2°.
7:2 = 3, остаток 1; 231 = (((((3 х2 + 1)х2 + 0)х2 + 0)х2 + + 1)х2+ 1)х2 + 1 = 3х26 + 1 х25+ 1 х22+ 1 х 21 + 1 х 2°.
3:2= 1; остаток 1; далее процесс продолжать нельзя, так как 1 не делится нацело на 2.
231 = ((((((1 х2+1)х2+1)х2 + 0)х2 + 0)х2+1)х2+1)х х 2 + 1 = 1 х 27 + 1 х 26 + 1 х 25 + 1 х 22 + 1 х 21 + 1 х 2°.
Таким образом, последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.
231 = 1 х27+ 1 х26+ 1 х 25+ 0 х 24+ 0 х 23+ 1 х22+ 1 х 21+ + 1x2°= 11100111^.
Эти выкладки можно сократить, записав процесс деления следующим образом:

|
| 231 |
231(10)=11100111(2)
Читая частное и остатки от деления в порядке, обратном получению, получим двоичную запись числа. Такой способ перевода чисел называется правилом (алгоритмом) последовательного деления, очевидно, что он применим для любого основания.
Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения, которое также рассмотрим на примере. Переведем 0,8125 из десятичной системы в двоичную систему счисления.
Умножим его на 2, т.е. 0,8125 х 2 = 1,625 или 0,8125 = (1 + 0,625) х х2"1 = 1x2-' + 0,625х2-1.
Аналогично 0,625 = (1 + 0,25) х 2~1 или
0,8125 = 1 х 2'1 + (1 + 0,25) х 2'1 х 2~] = 1 х 2~] + 1 х 2~2 + + 0,25 х 2~2, но 0,25 = 0,5 х 2~].
0,8125 = 1 х 2-1 + (1 + 0,5 х 2~1) х 2'1 х 2~' = 1 х 2~! + 1 х 2~2 + + 0,5 х 2~3, но 0,5 = 1 х 2~1.
0,8125 = 1 х 2'1 + 1 х 2-2+ 1 х 2-1 х 2'3 = 1 х 2-' + 1 х 2-2+ 1 х 2~4.
В итоге получаем, что 0,8125(10) = 1 х 2'1 + 1 х 2~2 + 1 х 2~4 = = 0,1101(2). Сокращая выкладки, получим правило (алгоритм) последовательного умножения',
Попутно заметим, что в десятичной системе счисления правильная дробь переводится в десятичную дробь в конечном виде только в том случае, если ее знаменатель в качестве множителей имеет толь-
ко степени двоек и пятерок, т.е. дробь имеет вид т п. Все же ос-
тальные дроби переводятся в бесконечные периодические дроби. Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки, т.е. большинство десятичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.
Если ведутся приближенные вычисления, то последний разряд является сомнительным, и для обеспечения в приближенных вычислениях одинаковой точности в двоичной и десятичной записях числа без бесконечных дробей, достаточно взять число двоичных разрядов в (1о§210 ~ 3,3) 4 раза больше, чем десятичных.
Между двоичной системой счисления, с одной стороны* и восьмеричной и шестнадцатеричной (заметим, 8 и 16 — есть третья и четвертая степени двойки) — с другой, существует связь, позволяющая легко переводить числа из одной системы в другую. Рассмотрим на примере:
231,8125(|0)= 11100111, 1101(2)= 1 х 27+ 1 х 26 + 1 х 25 + 1 х 22 + + 1 х 2' + 1 х 2°+ 1 х 2-1 + 1 х 2'2+1 х 2Л
Для перевода в шестнадцатеричную систему счисления сгруппируем целую и дробную части в группы по четыре члена и вынесем в каждой группе за скобки множители, кратные 24. Получим:
(1 х 23 + 1 х 22 + 1 х 21 + 0 х 2°) х 24 + (1 х 23 + 1 х 22 + 1 х 21 + + 1 х 2°) + (1 х 23 + 1 х 22 + 0 х 21 + 1 х 2°) х 2-4 = (1 х 23 + 1 х 22 + + 1 х 21 + 0) х 161 + (1 х 22 + 1 х 21 + 1 х 2°) х 16° + (1 х 23 +1 х 22 + + 0 х 21 + 1 х 2°) х 16-' = 14 х 16' + 7 х 16° + 13 х 16'1 = Е7.П
(16)
Резюмируя, заключаем: для того, чтобы перевести число из двоичной системы в шестнадцатеричную, надо от десятичной запятой вправо и влево выделить группы по четыре цифры (они называются тетрадами), и каждую группу независимо от других перевести в одну шестнадцатеричную цифру.
Аналогичное правило для восьмеричной системы читатель выведет сам.
Представление чисел В ЭВоичном коЭе
Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах — минимальных по размеру адресуемых (т.е. к ним возможно обращение) ячейках памяти. Очевидно, адресом числа следует считать адрес первого байта. В байте может содержаться произвольный код из восьми двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число.
Действительное число многообразно в своих «потребительских свойствах». Числа могут быть целые точные, дробные точные, рациональные, иррациональные, дробные приближенные, числа могут быть положительными и отрицательными. Числа могут быть «карликами», например, масса атома, «гигантами», например, масса Земли, реальными, например, количество студентов в группе, возраст, рост. И каждое из перечисленных чисел потребует для оптимального представления в памяти свое количество байтов.
Очевидно, единого оптимального представления для всех действительных чисел создать невозможно, поэтому создатели вычислительных систем пошли по пути разделения единого по сути множества чисел на типы (например, целые в диапазоне от... до..., приближенные с плавающей точкой с количеством значащих цифр... и т.д.). Для каждого в отдельности типа создается собственный способ представления.
Целые числа. Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера.
| Число | Двоичный код числа |
| 0000 0000 | |
| • • • | • • • |
| 1111 1111 |
В такой форме представления легко реализуется на компьютерах двоичная арифметика.
Если нужны и отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит; ноль интерпретируется как плюс, единица как минус. В таком случае одним байтом может быть закодированы целые числа в интервале от —127 до +127, причем двоичная арифметика будет несколько усложнена, так как в этом случае существуют два кода, изображающих число ноль 0000 0000 и 1000 0000, и в компьютерах на аппаратном уровне это потребуется предусмотреть. Рассмотренный способ представления целых чисел называется прямым кодом. Положение с отрицательными числами несколько упрощается, если использовать, так называемый, дополнительный код. В дополнительном коде положительные числа совпадают с положительными числами в прямом коде, отрицательные же числа получаются в результате вычитания из 1 0000 0000 соответствующего положительного числа. Например, число —3 получит код 1 0000 0000 00000011 1111 1101
В дополнительном коде хорошо реализуется арифметика, так как каждый последующий код получается из предыдущего прибавлением единицы с точностью до бита в девятом разряде. Например, э —.$ э &~ ^ ^/* 0000 0101 1111 1101
1 0000 0010, т.е., отбрасывая подчеркнутый старший разряд, получим 2.
Аналогично целые числа от 0 да 65536 и целые числа от —32768 до 32767 в двоичной (шестнадцатеричной) системе счисления представляются в двухбайтовых ячейках. Существуют представления целых чисел и в четырехбайтовых ячейках.
Действительные числа. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Однако в компьютерах числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разря-
2. Информатика
О о
дов. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные. В большинстве систем программирования в написании действительных чисел целая и дробная части разделяются не запятой, а точкой.
Для представления действительных чисел, как очень маленьких, так и очень больших, удобно использовать форму записи чисел в виде произведения
X = т • др,
где т — мантисса числа;
Я — основание системы счисления;
р — целое число, называемое порядком.
Такой способ записи чисел называется представлением числа с плавающей точкой.
То есть число 4235,25 может быть записано в одном из видов:
4235,25 = 423,525-101= 42,3525-102 = 4,23525-103 = 0,423525-104.
Очевидно, такое представление не однозначно. Если мантисса 1 / я < |т| < я (0,1 < |т| < 1 для десятичной системы счисления), то представление числа становится однозначным, а такая форма называется нормализованной. Если «плавающая» точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т.е. максимальная точность.
Действительные числа в компьютерах различных типов записываются по-разному, тем не менее существует несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру. Рассмотрим на примере числа, занимающего 4 байта.
32 31 30
24 23 22 21
| \ | Смещенный порядок | Мантисса | |||||||||||||

Знак мантиссы
Первый бит двоичного представления используется для кодирования знака мантиссы. Следующая группа бит кодирует порядок числа, а оставшиеся биты кодируют абсолютную величину мантиссы. Длины порядка и мантиссы фиксируются.
Порядок числа может быть как положительным, так и отрицательным. Чтобы отразить это в двоичной форме, величина порядка представляется в виде суммы истинного порядка и константы, равной абсолютной величине максимального по модулю отрицательного порядка, называемой смещением. Например, если порядок может принимать значения от —128 до 127 (8 бит), тогда, выбрав в качестве смещения 128, можно представить диапазон значений порядка от 0 (-128+128, порядок + смещение) до 255 (127+128),
Так как мантисса нормализованного числа всегда начинается с нуля, некоторые схемы представления его лишь подразумевают, используя лишний разряд для повышения точности представления мантиссы.
Использование смещенной формы позволяет производить операции над порядками как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.
Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, пред ставимого в компьютере при заданном формате.
Вещественные числа в памяти компьютера, в зависимости от требуемой точности (количества разрядов мантиссы) и диапазона значений (количества разрядов порядка), занимают от четырех до десяти байтов. Например, четырехбайтовое вещественное число имеет 23 разряда мантиссы (что соответствует точности числа 7—8 десятичных знаков) и 8 разрядов порядка (обеспечивающих диапазон значений 10±38). Если вещественное число занимает десять байтов, то мантиссе отводится 65 разрядов, а порядку — 14 разрядов. Это обеспечивает точность 19—20 десятичных знаков мантиссы и диапазон значений 10±4931.
Понятие типа данных. Как уже говорилось, минимально адресуемой единицей памяти является байт, но представление числа требует большего объема. Очевидно, такие числа займут группу байт, а
адресом числа будет адрес первого байта группы. Следовательно, произвольно взятый из памяти байт ничего нам не скажет о том, частью какого информационного объекта он является — целого числа, числа с плавающей запятой или команды. Резюмируя вышесказанное, можно сделать вывод, что кроме задачи представления данных в двоичном коде, параллельно решается обратная задача — задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные.
Для представления основных видов информации (числа целые, числа с плавающей запятой, символы, звук и т.д.) в системах программирования используют специального вида абстракции — типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных. В дальнейшем для каждого типа данных будут определены и соответствующие ему операции обработки.
1.3,2, ЛреЭстоВление символьный
и текстоВын Эаннын В ЭВоичном коЭе
Для передачи информации между собой люди используют знаки и символы. Начав с простейших условных жестов, человек создал целый мир знаков, где главным средством общения стал язык (т.е. речь и письменность). Слово есть минимальная первичная единица языка, представляющая собой специальный набор символов и служащая для наименования понятий, предметов, действий и т.п. Следующим по сложности элементом языка является предложение — конструкция, выражающая законченную мысль. На основе предложений строится текст. Текст (от лат. 1ехШ8 — ткань, соединение) - высказывание, выходящее за рамки предложения и представляющее собой единое и целое, наделенное внутренней структурой и организацией в соответствии с правилами языка.
С появлением вычислительных машин стала задача представления в цифровой форме нечисловых величин, и в первую очередь — символов, слов, предложений и текста.
Символы. Для представления символов в числовой форме был предложен метод кодирования, получивший в дальнейшем широкое распространение и для других видов представления нечисловых дан-
ных (звуков, изображений и др.). Кодом называется уникальное беззнаковое целое двоичное число, поставленное в соответствие некоторому символу. Под алфавитом компьютерной системы понимают совокупность вводимых и отображаемых символов. Алфавит компьютерной системы включает в себя арабские цифры, буквы латинского алфавита, знаки препинания, специальные символы и знаки, буквы национального алфавита, символы псевдографики — растры, прямоугольники, одинарные и двойные рамки, стрелки. Первоначально для хранения кода одного символа отвели 1 байт (8 битов), что позволяло закодировать алфавит из 256 различных символов. Система, в которой каждому символу алфавита поставлен в соответствие уникальный код, называется кодовой таблицей. Разные производители средств вычислительной техники создавали для одного и того же алфавита символов свои кодовые таблицы. Это приводило к тому, что символы, набранные с помощью одной таблицы кодов, отображались неверно при использовании другой таблицы. Для решения проблемы многообразия кодовых таблиц в 1981 г. Институт стандартизации США принял стандарт кодовой таблицы, получившей название А8СП (Атепсап 81апс1агс1 Соёе оГ 1пГогта1юп 1п1егсЬап§е — американский стандартный код информационного обмена). Эту таблицу использовали программные продукты, работающие под управлением операционной системы М8-ОО8, разработанной компанией МюгоБой по заказу крупной фирмы — производителя персональных компьютеров 1ВМ (1п1егпа1юпа1 Визшезд МасЫпе). Широкое распространение персональных компьютеров фирмы 1ВМ привело к тому, что стандарт А8СП приобрел статус международного.
В таблице А8СП содержится 256 символов и их кодов. Таблица состоит из двух частей: основной и расширенной. Основная часть (символы с кодами от 0 до 127 включительно) является базовой, она в соответствии с принятым стандартом не может быть изменена. В нее вошли: управляющие символы (им соответствуют коды с 1 по 31), арабские цифры, буквы латинского алфавита, знаки препинания, специальные символы (табл. 1.1).
Расширенная часть (символы с кодами от 128 до 255) отдана национальным алфавитам, символам псевдографики и некоторым специальным символам. В соответствии с утвержденными стандар-
Тоблииа 1.1. Базовая часть таблииы коЭоВ О/СИ
| Код | Код | Код | Код | Код | Код | Код | Код | ||||||||
| пробел | > | о | Р | \ | Ь | ||||||||||
| ! • | _ | Е | ] | » | и | ||||||||||
| *• | • | • • | Р | В | .л. | • | V | ||||||||
| « | / | • * | ~ | 1< | « | ||||||||||
| $ | < | Н | Т | X | |||||||||||
| •/, | — | I | и | а | т | У | |||||||||
| & | > | и | V | Ь | п | ||||||||||
| У | • | К | И | с | { | ||||||||||
| ( | @ | К | с! | Р | |||||||||||
| ) | я | М | V | е | д | } | |||||||||
| * | в | N | г | ? | г | Л" | |||||||||
| -1- | с | [ | и |
тами эта часть таблицы изменяется в зависимости от национального алфавита той страны, где она используется, и способа кодирования. Именно поэтому, при наименовании программ, документов и других объектов желательно использовать латинские буквы, содержащиеся в основной, неизменяемой части таблицы, так как русскоязычные имена при несоответствии таблиц кодирования будут неверно отображаться. Например, операционная система \ЭДпс1о\У!5 поддерживает большое число расширенных таблиц для различных национальных алфавитов. В России наиболее распространенной кодовой таблицей алфавита русского языка является «латиница \ЭДпс1о\У5 1251» (табл. 1.2).
В качестве другого примера рассмотрим расширенную таблицу «ГОСТ—альтернативная» (табл. 1.3), на смену которой пришла «латиница Щпёоте 1251».
Во многих странах Азии 256 кодов явно не хватило для кодирования их национальных алфавитов. В 1991 г. производители программных продуктов и организации, утверждающие стандарты, пришли к соглашению о выработке единого стандарта. Этот стандарт построен по 16 битной схеме кодирования и получил название УМ1СООЕ. Он позволяет закодировать 216= 65536 символов, которых достаточно для кодирования всех национальных алфавитов в одной таблице. Так как каждый символ этой кодировки занимает два байта (вместо одного, как раньше), все текстовые документы, пред-
Таблииа 1.2. Расширенная таблииа «латинииа Ш|пс1ошу 1251»
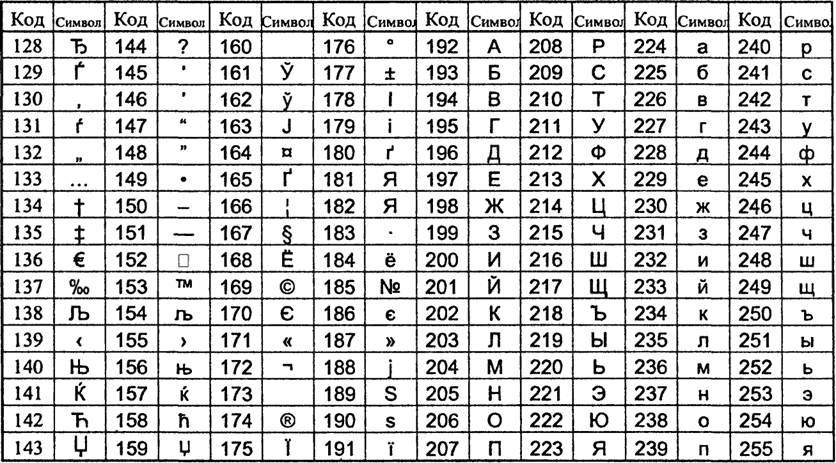
Таблииа 1.3. Расширенная таблииа «ГОСТ-альтернатиВная»

ставленные в 1Ж1ССЮЕ, стали длиннее в два раза. Современный уровень технических средств нивелирует этот недостаток 1Ж1ССЮЕ.
Текстовые строки. Текстовая (символьная) строка — это конечная последовательность символов. Это может быть осмысленный текст или произвольный набор, короткое слово или целая книга. Длина символьной строки — это количество символов в ней. Записывается в память символьная строка двумя способами: либо число, обозначающее длину текста, затем текст, либо текст, затем — разделитель строк.
Текстовые документы. Текстовые документы используются для хранения и обмена данными, но сплошной, не разбитый на логические фрагменты текст воспринимается тяжело. Структурирование теста достигается форматированием — специфическим расположением текста при подготовке его к печати. Для анализа структуры текста были разработаны языки разметки, которые устанавливают текстовые метки (маркеры или теги), используемые для обозначения частей документа, записывают вместе с основным текстом в текстовом формате. Программы, анализирующие текст, структурируют его, считывая теги.
1.3.3. Представление зВукоВын Эаннын В ЭВоичном коЗе
Звук — это упругая продольная волна в воздушной среде. Чтобы ее представить в виде, читаемом компьютером, необходимо выполнить следующие преобразования (рис. 1.4.). Звуковой сигнал преобразовать в электрический аналог звука с помощью микрофона. Электрический аналог получается в непрерывной форме и не пригоден для обработки на цифровом компьютере. Чтобы перевести сигнал в цифровой код, надо пропустить его через аналого-цифровой преобразователь (АЦП). При воспроизведении происходит обратное преобразование — цифро-аналоговое (через ЦАП). Позже будет показано, что конструктивно АЦП и ЦАП находятся в звуковой карте компьютера.
Во время оцифровки сигнал дискретизируется по времени и по уровню (рис. 1.5.). Дискретизация по времени выполняется следующим образом: весь период времени Т разбивается на малые

|
Рис. 1.4. Схема обработки звукового сигнала

|
| X I |
Рис. 1.5. Схема дискретизации звукового сигнала
интервалы времени А1, точками I,, 12,... 1п. Предполагается, что в течение интервала А1 уровень сигнала изменяется незначительно и может с некоторым допущением считаться постоянным. Величина v = 1/Л1 называется частотой дискретизации. Она измеряется в герцах (Гц) — количество измерений в течение секунды.
Дискретизация по уровню называется квантованием и выполняется так: область изменения сигнала от самого малого значения X
гшп
до самого большого значения Хтах разбивается на N равных квантов, промежутков величиной
Точками Х„ Х2,... Хп. X, = Х^ + АХ • (I - 1).
Каждый квант связывается с его порядковым номером, т.е. целым числом, которое легко может быть представлено в двоичной системе счисления. Если сигнал после дискретизации по времени (напомним, его принимаем за постоянную величину) попадает в промежуток Хм < X < X, то ему в соответствие ставится код 1.
Возникают две задачи:
— первая: как часто по времени надо измерять сигнал,
Поиск по сайту: