Пример 6.5

Одним из наиболее распространенных алгоритмов, встречаю­щихся в литературе по информатике, является алгоритм Евклида — алгоритм нахождения наибольшего общего делителя двух натураль­ных чисел тип (рис. 6.9).

Начало

I

/ Ввод V / т,п/

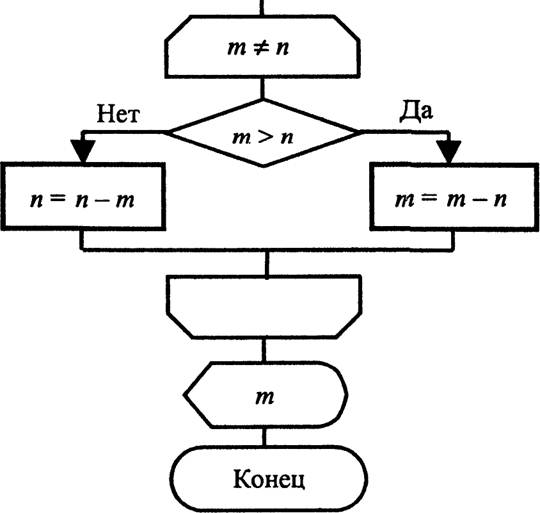
Рис. 6.9. Блок-схема алгоритма Евклида

Опишем его на псевдокоде:

1. Ввод натуральных чисел тип.

2. Пока т * п делать.

2.1. Если т>п,тот=т — п,
иначе п—п — т.

2.2. Переход к шагу 2.

3. Вывод т (найденный наибольший общий делитель).

4. Конец.

11икл с постуслоВием

Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с пред­условием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполне­ние команды прекращается. Блок-схема данной конструкции пред­ставлена на рис. 6.10 двумя способами: с помощью условного блока а и с помощью блока управления б.

Тело цикла

Тело цикла

I

Условие

а

Рис. 6.10. Блок-схема цикла с постусловием

Поиск по сайту: