Наиболее распространённые законы распределения вероятностей

В рамках теории вероятностей на основании обобщения знаний о случайных явлениях в природе и человеческом обществе построен ряд моделей распределения вероятностей, которые в некоторых ситуациях удовлетворительно описывают исследуемые закономерности. Для каждой модели (закона распределения) установлены и условия её применимости. Если при рассмотрении некоторого явления исследователь считает, что имеющие место условия совпадают с условиями применимости того или иного закона, то можно воспользоваться соответствующим законом распределения.

Биномиальное распределение.

Пусть реализуется схема опы­тов Бернулли: проводится n одинаковых независимых опытов, в каждом из которых событие А может появиться с постоянной вероятностью р. Число появлений события А в этих n опытах есть дискретная случайная величина X, возможные значения которой: 0; 1; 2; …; m; …; n.

Законом распределения этой случайной величины является формула, определяющая вероятность того, что в конкретной серии из n опытов событие А появляется ровно m раз. Такая вероятность, а, следовательно, закон распределения, задается формулой Бернулли, или биномиальным законом распределения:

Р(Х = m) = Р_m,n = С_n^m × p^m ×(1 – p) ^n-m.

Числовые характеристики случайной величины X, распре­деленной по биномиальному закону:

m_x = n × p, D_x = n × p ×(1 – p), s_x = .

Задача 24. Какова вероятность того, что при десяти бросках игральной кости 3 очка выпадут ровно 2 раза?

Решение.

Здесь n = 10, m = 2, р = 1/6, q = 1 – р = 5/6.

Искомая вероятность: Р _2,10 = С ₁₀²×(1/6)²×(5/6)⁸» 0,29.·

Задача 25. Найти вероятность того, что при 10-кратном бросании монеты орёл выпадет ровно 5 раз.

Решение.

Здесь вероятность выпадения орла при одиночном испытании р =1/2; отсюда q = 1 – p = 1/2.

По формуле Бернулли получаем:

Р _5,10 = С ₁₀⁵×(1/2)⁵×(1/2)⁵ .·

Задача 26. Автомобиль, подъезжая к перекрёстку, может продолжить движение по любой из трёх дорог: А, В или С – с одинаковой вероятностью. К перекрёстку подъезжа­ют пять автомобилей. Найти среднее число автомашин, которое поедет по дороге А, и вероятность того, что по дороге В поедет три автомобиля.

Решение.

Число автомашин, проезжающих по каждой из дорог, является случайной величиной.

Если предположить, что все подъезжающие к перекрёстку автомобили совершают поез­дку независимо друг от друга, то эта случайная величина рас­пределена по биномиальному закону с n = 5 и р = 1/3.

Следовательно, среднее число автомашин, которое просле­дует по дороге А, есть m = 5/3, а искомая вероятность:

Р(Х =3 ) = С ₅³×(1/3)³×(2/3)²» 0,165.·

Распределение Пуассона.

Пусть событие А может появиться в любой момент времени. При этом выполнены следующие условия:

1) события происходят независимо друг от друга;

2) появление события А на данном отрезке времени не зави­сит от расположения временного отрезка на оси времени;

3) вероятность появления события А за бесконечно малый интервал времени Dt более одного раза есть бесконечно малая величина по сравнению с Dt (в этой связи закон Пуассона назы­вают законом редких событий).

Число появлений события А за выбранный промежуток вре­мени t подчиняется закону Пуассона:

P(X = m) = ,

где l – среднее число событий А, появляющихся за едини­цу времени.

Этот закон однопараметрический, т.е. для его задания тре­буется знать только один параметр l. Можно показать, что математическое ожидание и дисперсия в законе Пуассона чис­ленно равны: m_x = D_x = l.

Задача 27. При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0,01. Какова вероятность, что в партии 100 изделий этой продукции 2 изделия будут нестандартными?

Решение.

1) Здесь вероятность р = 0,01 мала, а число n = 100 велико, причём m = n × р = 100 × 0,01 = 1.

2) Используя закон Пуассона для искомой вероятности, получаем следующее значение:

P _2,100 .·

Одним из классических примеров применения закона Пуас­сона является описание числа запросов на соединение, посту­пающих на телефонную станцию.

Задача 28. Пусть в середине рабочего дня среднее число зап­росов равняется 2 в секунду. Какова вероятность того, что 1) за секунду не поступит ни одной заявки, 2) за две секунды поступит 10 заявок?

Решение.

Поскольку правомерность применения закона Пу­ассона не вызывает сомнения и его параметр задан (l = 2), то решение задачи сводится к прямому применению формулы Пуассона.

1) t = l, m = 0: P(Х =0 ) 0,135.

2) t = 2, m = 10: P(Х =10 ) 0,005.·

Закон равномерной плотности.

Пусть непрерывная случайная ве­личина Х может принимать лю­бые значения лишь на отрезке [ а, b ] и нет оснований считать, что появление одних возможных зна­чений вероятней других. При вы­полнении этих условий говорят, что случайная ве­личина Х распределена с равномер­ной плотностью. В этой связи целесообразно считать, что плот­ность вероятности f(x) имеет вид:

.

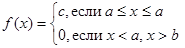График такой функции представлен на рис. 3.

Рис. 3. График равномерной плотности распределения

Поскольку площадь, ограниченная любой кривой распределения, равна1,легко найти значение константы с из равенства с × (b – а) = 1, с = 1/(b – a).

Теперь можно сказать, что случайная величина Х распреде­лена на отрезке [ а, b ] равномерно, если:

.

Основные числовые характеристики равномерно распреде­ленной случайной величины:

,

,

.

Задача 29. Минутная стрелка часов делает скачок на сосед­нее деление, когда реальное время превышает указывае­мое значение на полминуты. При взгляде на часы фикси­руется показываемое ими время. Какова средняя ошибка в показаниях таких часов и каков разброс этой ошибки?

Решение.

В каждый момент времени показания часов есть случайная величина, показывающая реальное время с некото­рой ошибкой. Взгляд на часы производится в случайно выб­ранный момент, поэтому целесообразно предположить, что ошибка в показаниях часов имеет равномерную плотность распределения.

Т.к. рассогласование между реальным временем и пока­заниями часов находится в пределах от –0,5 до +0,5, то следует положить а = –0,5, b = +0,5. Следовательно:

.

Это означает, что систематическая ошибка отсутствует и .·

Нормальный закон распределения.

Непрерывная случайная величина Х распределена по нормальному закону, если её плот­ность вероятности описывается функцией:

,

где m – математическое ожидание; s – среднеквадратическое отклонение.

Соответственно, функция распределения равна:

.

График плотности вероятности для нормального закона приведен на рис. 2. Нормальный закон возникает в тех случаях, когда случайная величина Х есть сумма большого числа слу­чайных величин, распределенных по произвольному закону, но каждая из них не является доминирующей.

Наиболее ярким примером является ошибка, возникающая при различных из­мерениях (длины, объёма, массы и т.п.). Действительно, если измерительный прибор хорошо отрегулирован, то он не даёт существенных систематических ошибок (иначе его следовало бы отрегулировать). Получаемые же при каждом измерении ошибки складываются из влияния множества факторов, устра­нить которые практически невозможно. Они зависят от изме­нений температуры, давления, влажности и т.п. Иногда ошиб­ки складываются, усиливая друг друга, а иногда – компенсируя одна другую.

Для вычислений вероятности попадания случайной величи­ны в заданный промежуток возможных значений используется приведённая функция плотности вероятности и приведённая функция распределения – функция распределения для так на­зываемой нормированной случайной величины с m = 0 и s = 1.

Нормированная случайная величина получится, если сделать замену x ₁ = (х – m)/ s.

, F ^*(х) .

Функции f (x) и Ф* (х) табулированы.

Функция Ф* (х) обла­дает следующими свойствами:

Ф* (0) = 0,5, Ф* (х) = 1 – Ф* (– х).

При вычислениях связанных с нормальным законом часто используют интеграл Лапласа, который также табулирован:

F (х) ;

при этом следует иметь ввиду, что Ф* (х) = Ф (х) + 0,5.

Если случайная величина распределена по нормальному закону с параметрами m и s, то:

P (a £ x < b) = Ф^* – Ф^* = Ф – Ф . (1)

Задача 30. При изготовлении бумаги наблюдается откло­нение её плотности от номинала, равного 100 г на квад­ратный метр. Найти ве­роятность того, что плотность бумаги будет отличаться от номинала не более, чем на 2 г, и не менее, чем на 3 г, если считать, что плотность бумаги есть нормально распределённая величина с s = 5 г.

Решение.

Используем формулу (1):

Р (97 < х < 102) = Ф^* – Ф^* = Ф^* (0,4) – Ф^* (–0,6) = 0,6554 – 0,2743 = 0,3811.·

На практике удобно использовать правило«три сигма», ко­торое гласит: с вероятностью, большей, чем 0,997, случайная величина, распределённая по нормальному закону, будет при­нимать значения в промежутке (m_x – 3 s_x, m_x + 3 s_x).

Задача 31. Имеется партия изделий, в которой могут попа­даться качественные и бракованные. Число бракованных изделий – нормально распределённая случайная величи­на, характеризующаяся так: среднее число бракованных изделий (математическое ожидание) составляет 12 % и среднеквадратическое отклонение – 3 %. Отобрано 100 изделий. Какое число бракованных изделий окажется среди них?

Решение.

Должно быть понятным, что точно ответить на такой вопрос в принципе невозможно.

Однако, используя пра­вило «три сигма», легко найти следующий ответ: можно быть практически уверенным, что бракованных деталей будет не менее 12 – 3 × 3 = 3 и не более 12 + 3 × 3 = 21.

Формально это мож­но записать так Р (3< х <22) ³ 0,997.·

Поиск по сайту: