Функция распределения. Функция плотности вероятности

Существует много различных форм законов распределения. Наиболее универсальной из форм яв­ляется функция распределения.

Функцией распределения F(x), или интегральным законом распределения, случайной величины Х называется функция F(x) = Р( –¥< х < х), задающая вероятность выполнения неравенства Х < х.

Функция распределения определена для случайных величин любого типа: дис­кретных и непрерывных.

Определение функции рас­пределения имеет нагляд­ную геометрическую интерпретацию. Если значения случайной величины Х рассматри­вать как точки числовой оси Ох, то F(x) есть вероятность события, состоящего в том, что наблюдаемое значение случайной величины Х принадлежит интервалу (–¥, х), т.е. находится левее точки х.

Свойства функции распределения:

1) F(x) – неотрицательная функция, значения которой зак­лючены между 0 и 1, т.е.

0 £ F(x) £ 1;

2) F( –¥ ) = 0;

3) F (+¥) = 1;

4) F(x) – неубывающая функция своего аргумента, т.е. если х ₁ > х ₂ то F(x ₁ ) > F(x ₂ );

5 ) Р(а £ X £ b) = F(b) – F(a).

Введение функции распределения позволяет дать точное оп­ределение непрерывной случайной величины: случайная величи­на называетсянепрерывной, если её функция распределения есть непрерывная функция с кусочно-непрерывной производной.

Непрерывную случайную величину удобнее описывать законом распределения, который называют функцией плотности вероятности, или дифференци­альным законом.

Пусть Х – непрерывная случайная величина, имеющая функцию распределения F(x). Если эта функция диф­ференцируема, то можно рассматривать ее производную F¢(x) = j(х). Функция j(х) называетсяплотностью вероятности случайной вели­чины Х, или функцией распре­деления вероятностей (рис. 1).

Рис. 1. График функции плотности вероятности

Вероятность Р(а £ X £ b) = 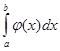. Геометрически эта вероятность представляет собой площадь S криволинейной трапеции, ограниченной графиком плотности вероятности y = j(х), осью Ох и двумя ординатами x = a и x = b (см. рис. 1).

Полагая a = –¥, b = x и обозначая для ясности переменную интегрирования х другой буквой, например t (это законно для определённого интеграла), получаем функцию распределения:

F(x) = Р( –¥< х < х) = .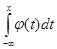

Свойства функции плотности вероятности:

1) j(х) – неотрицательная функция, j(х) ³ 0;

2) интеграл в бесконечных пределах от функции плотности вероятности (если она задана на всей числовой оси) равен 1:

F( ¥ ) = Р( –¥< х <+¥ ) = 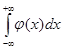= 1 (это свойство называется условием нормировки).

Замечание. Если случайная величина задана только на от­резке [ х ₁, x ₂], то пределы интегрирования изменя­ются на х ₁ и х ₂:

F( ¥ ) = Р(х ₁< х < х ₂ ) = 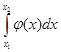= 1.

Поиск по сайту: