АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Расчет наращенной суммы декурсивным и антисипативным способами

Читайте также:
  1. I. Расчет накопительной части трудовой пенсии.
  2. I. Расчет производительности технологической линии
  3. I. Расчет размера страховой части трудовой пенсии.
  4. II. Расчетная часть задания
  5. Аккредитивная форма расчетов
  6. АКТИВНО-ПАССИВНЫЕ СЧЕТА РАСЧЕТОВ
  7. Алгоритм расчета
  8. Алгоритм расчета дисперсионных характеристик плоского трехслойного оптического волновода
  9. Алгоритм расчета температуры горения
  10. Амортизация как целевой механизм возмещения износа. Методы расчета амортизационных отчислений.
  11. Анализ общей суммы затрат и з-т на 1 руб. прод-ции
  12. Анализ общей суммы затрат на производство продукции
Способ начисления процентов Простая процентная ставка Сложная процентная ставка
1. Декурсивный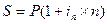
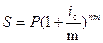
2. Антисипативный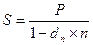

 

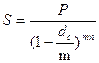
где S – наращенная сумма;

P – первоначальная сумма;

in, ic – простая и сложная годовая процентная ставка;

n – продолжительность периода, в годах;

m – количество интервалов начисления в год;

dn, dc – простая и сложная годовая учетная ставка.

Определение современной величины Р известной наращенной суммы называется дисконтированием, а определение величины наращенной суммы S при известной первоначальной сумме – компаундингом.

В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный процент.

Точный процент получают, когда за временную базу берут фактическое число дней в году (365 или 366) и точное число дней ссуды.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)