 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ПОИСКИ ПЕРИОДИЧНОСТИ
Нетрудно заметить, что при перемещении заряда от точки 1 до точки 3 его действие сначала возрастает от 0 до Lэ, азатем уменьшается до нуля.Далее, при двидении этого заряда от точки 3 до 1 такое изменение действия, как нетрудно проверить, повторяется. Поскольку, как отмечалось выше, заряд то входит в «поле зрения» центра М, то исчезает, максимальное значение действия d, а, следовательно, и момента импульса Lэ равно постоянной Планка h:
Lэ =h, (11.11,б)
В силу закона сохранения момента импульса, при переходе от орбиты, содержащей максимальное число n эпициклов к орбите с числом (n+1) эпицикл момент импульса движения заряда m по дифференту возрастёт на h (как видно на рисунке 11.7, поворот заряда по дифференту направлен в сторону, противоположную его вращению по эпициклу). Следовательно, момент орбитального импульса при (n+1) эпициклах отличается от момента импульса при n эпициклах на величину h:
mvn+1rn+1 –mvnrn =h.
Следовательно, момент орбитального импульса заряда m равен целому числу h:
mvr =nh. (11.11,в)
Согласно (11.10,б и в) получаем дискретные значения r,WΣ:
r =4πε0 h2 n2/mq1q2; WΣ = h2n2/2mr; (11.11,г)
Число n называется радиальным квантовым числом. Судяпо сказанному выше, это число обязательно должно быть больше kα.max или,что тоже самое, kβ:
kβ < n. (11.11,д)
Всё сказанное выше о траектории движения заряда m справедливо только при условии, что точно известна точка начала движения заряда y0 (см. рис. 11.3,а). Однако, в силу принципа неопределённости, заряд может начать двигаться в любой другой точке. Поэтому точной траектории движения заряда m установить нельзя. Но все другие характеристики, выведенные выше, распространяются на все эти траектории. В частности,
| kα| ≤ kβ < n (11.12)
Те же самые соотношения можно получить,воспользовашись математическим формализмом, основанным на уравнеиии Шредингера (11.3,в).Для этого нужно, преобразовать его к сферическим координатам (см. рис.11.6,а).
(11.13,а)
Согласно [5] в сферических координатах (r,α, β):
(11.13,б)
где
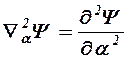(11.13,в)
Несмотря на кажущуюся сложность записи 
, решение уравнения (11.13,а) с учетом (11.13,б,в) ищется в достаточно простом виде:
(11.13,г)
где А - нормировочный коэффициент, Ψr, Ψβ и Ψα, - функции соответственно только от r, и β, α. Подставляя (11.13,б,в,г) в (11.13,а), получаем
(11.13,д)
Из (11.13,д) следует, что уравнение Шредингера в сферических координатах превратилось в три независимых друг от друга уравнения от α, β, r:
(11.14,а)
(11.14,б,в)
Столь сложная запись постоянных 
и 
в правой части выражений (11.14,б и в) связана с удобством их дальнейшего использования. Выражение (11.14,в) можно записать в виде обычного волнового уравнения:
решение, которого имеет вид:
(11.14,г)
Из требования однозначности решения вытекает то обстоятельство, что 
-целое число (Κα=0,±1;±2;…), именуемое магнитным квантовым числом [11]. Амплитуда Ψαm вычисляется, исходя из обычного требования (см.§ 11.2) равенства единице интеграла Ψ 2 
по всем значениям α:
═> 
Выражение (11.14,б) с учетом (11.14,г) имеет вид:
откуда получаем
(11.14,д)
где 
является присоединенной функцией Лежандра[5].
Амплитуда Ψβm вычисляется также, как и Ψαm, исходя из условия, что интеграл 
при изменении β в пределах от 0 до π равен единице. Опуская промежуточные выкладки, получаем [11]:
(11.14,е)
Из теории сферических функций [5] следует, что 
- целое положительное число (
=0,1,2,…), а
(11.14,ж)
Величина 
именуется азимутальным квантовым числом.
И, наконец, для определения зависимости распределении вероятности нахождении точки m от радиуса r преобразуем выражение (11.14,а):
Это уравнение также решается с применением сферических функций [5]. В данном случае используются полиномы Лагерра
где 
(11.14,з)
После довольно громоздких, но непринципиальных промежуточных выкладок получаем
(11.14,и)
где n целое число, именуемое радиальным квантовым числом, иногда – главным квантовым числом(n=1,2,…, Kβ=0,1,…, n -1).
Как видим, у функции 
несколько кратных n решений. Каждому из этих решений соответствует свое дискретное значение суммарной энергии
(11.15)
В том случае, когда 
отличается от какого-либо из этих значений, частица m излучает в виде электромагнитной волны избыток энергии до ближайшего меньшего по формуле (11.15). После этого она оказывается «размазанной» в пространстве в соответствии с значениями Ψα, Ψβ и Ψr. О том, как двигается частица m в пределах соответствующего участка пространства, точно сказать невозможно. Скорее всего, это хаотическое блуждание, в результате которого образуется облако с распределенной внутри него массой и зарядом.
Вопросы по одиннадцатой главе:
1. Почему в микромире возникает неопределенности при измерении положения (координат) частиц и их скоростей?
2. Сформулируйте принцип неопределенности.
3. Что такое волна вероятности?
4. Что такое волновой пакет?
5. Где в пространстве находится частица, двигающаяся с постоянной скоростью?
6. Сформулируйте уравнение Шредингера в ортогональных координатах.
7. Запишите уравнения Шредингера в сферических координатах.
8. Что такое магнитное, орбитальное и главное квантовое число?
9. Отличается ли энергия электронов, имеющих одинаковое главное квантовое число, но разные магнитные и орбитальные числа?
10. Сколько электронов в атоме имеют одинаковые все квантовые числа?
11. Как объяснить физически, почему электроны в атоме располагаются на строго определённых, заранее заданных орбиталях?
ПОИСКИ ПЕРИОДИЧНОСТИ
Представляя новую научную дисциплину – Теоретическую историю, – хотелось бы напомнить об ее истоках, о моменте ее зарождения. Возникла эта теперь уже большая наука из тщательных и планомерных поисков периодичности.
Периодичность для человечества тема не новая. Нам хорошо известна суточная периодичность (вращение Земли вокруг своей оси) и годовая периодичность (вращение Земли вокруг Солнца). У этих видов периодичности есть четкое и очевидное толкование. Менее понятны навязанные человечеству недельная периодизация, а также периодизация веков, под которыми, честно говоря, нет никакого разумного обоснования. Месячную периодизацию пытаются обосновать по-разному, не всегда убедительно, но при этом она достаточно очевидна и о ней будет сказано в «Избранных публикациях».
Очень интересно проследить существование 400-летней периодичности, которая явно или неявно предлагалась многими исследователями, пытавшимися обозначить эпохи в жизни человечества. Раннее Средневековье, позднее Средневековье, Возрождение, эпоха Прогресса... Любые попытки так или иначе вычленить эпохи приводили к проявлению именно 400-летних периодов. Этой периодизации будут посвящено восемь отдельных глав в разделе «Избранные публикации».
Максимальной убедительности и яркости удалось достичь автору при поиске. 12-дневной периодичности. И все-таки, при всей важности месячной, 400-летней или 12-дневной периодичности, для понимания исторических закономерностей наиболее важную роль сыграли поиски 4-летней периодичности, а также вытекающих из нее 12-, 36-, 72- и 144-летней периодичности. Именно в этих поисках сформировалось представление о решающей роли революционных переворотов (годы Политических, Экономических и Идеологических решений), о трех мирах (Запад, Восток, Империя), о трех типах 12-летних периодов, непрерывности Восточного и Западного ритма и изолированных Имперских циклах.
Важно также отметить, что принципиальным отличием данных поисков периодичности (от многочисленных аналогов как в мире, так и в России) стало отрицание догмы о непрерывности всякого ритма (Западный или Восточный ритм может быть прерван практически в любой момент ради ритма Империи). Также отринута догма о приблизительном размере всякого ритма. Исторические ритмы чрезвычайно точны, они просто-таки поражают жесткостью и неоспоримостью своего хода. Особенно в этом смысле потрясают Имперские синхроны, заставляющие, например, умирать, казалось бы, бессмертных вождей вторых фаз в те годы, месяцы и дни, которые продиктованы историческим графиком.
И еще хотелось бы добавить, что все поиски периодичности велись без предварительных установок, без попыток что-то под что-то подогнать, как, собственно, и должно быть во всякой науке. И если на базе данных поисков родилась достаточно жесткая и догматичная теория, то в этом нет вины автора, а есть всего лишь попытка наиболее точно и адекватно изложить вышедшие из поисков периодичности законы истории.
КНИГА ПЕРВАЯ
Поиск по сайту: