Общая задача линейного программирования

Мы рассмотрели сейчас предельно упрощенные примеры, преследуя исключительно иллюстративные цели, однако их анализ позволит осмыслить общие идеи и математические методы, лежащие в основе решения подобных задач.

В обоих примерах множество допустимых планов определяется точками выпуклого многогранника, полученного в результате пересечения полупространств, заданных линейными неравенствами (П.1) и (П.2). Линейная целевая функция при двух переменных задает на плоскости семейство параллельных прямых, при трех переменных – семейство параллельных плоскостей в трехмерном пространстве, а в случае n переменных – семейство параллельных (n- 1)–мерных пространств (гиперплоскостей) в n -мерном пространстве.

Линейные ограничения и линейная целевая функция появились в наших примерах благодаря предположению о пропорциональной зависимости переменных и постоянных факторов.

В силу этого подобный класс задач называют задачами линейного программирования.

Геометрически решение задачи линейного программирования сводится к следующим этапам:

а) определение области допустимых планов, т.е. построение соответствующего ограничениям многогранника;

б) перемещение гиперплоскости целевой функции в пространстве параллельно самой себе до тех пор, пока она не будет максимально (минимально) удалена от начала координат и при этом будет иметь хотя бы одну общую точку с многогранником допустимых планов.

Этой точкой, как мы видели, будет вершина многогранника, хотя может быть грань или ребро в случае параллельности гиперплоскости целевой функции какой-либо грани или ребру многогранника.

Координаты этой вершины и будут определять оптимальное решение. Если целевая гиперплоскость касается грани или ребра, то в этом случае получается множество оптимальных планов, имеющих одно и тоже максимальное (либо минимальное) значение целевой функции.

Из анализа решения примеров делаем важный вывод:

оптимальному плану соответствует точка в области допустимых планов (возможно неединственная), являющаяся вершиной многогранника допустимых планов. На этом основана идея метода решения задачи линейного программирования, заключающаяся в том, что для нахождения оптимального плана достаточно просматривать лишь вершины многогранника допустимых планов.

Решение (план), которому соответствует вершина многогранника, называется базисным. Для нахождения базисного плана необходимо решить систему из n линейных уравнений с n неизвестными.

Разработанный в 1949г. Дж. Данцигом симплекс-метод основан на последовательном переходе от одной вершины многогранника допустимых планов к соседней, в которой линейная целевая функция принимает лучшее (не худшее) значение до тех пор, пока не будет найдено оптимальное решение.

Рассмотренные выше примеры позволяют сформулировать общую задачу линейного программирования.

Дана система m линейных неравенств с n переменными

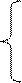a ₁₁ х ₁ + a ₁₂ х ₂ + …+ a_1n х_n £ b ₁

a ₂₁ х ₁ + a ₂₂ х ₂ + …+ a_2n х_n £ b ₂

……………………………….. (П.3)

a_{m 1} х ₁ + a _m2 х ₂ + …+ a_mn х_n £ b _m

и линейная функция

F = c ₁ х ₁ + c ₂ х ₂ + … + c_nх_n. (П.4)

Необходимо найти такое решение системы Х = (х ₁, х ₂,…, х_n), где

х _j ³ 0 (j =1,2,…n), (П.5)

при котором линейная функция F (2.4) принимает оптимальное (максимальное или минимальное) значение.

Система (П.3) называется системой ограничений, а функция F – целевой функцией, критерием или функцией цели.

Более кратко общую задачу линейного программирования можно представить в виде:

F = 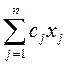à max(min)

при ограничениях:

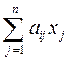£ b_i (i =1,2,…, m),

x_j ³ 0 (j =1,2,… n).

Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение системы ограничений (П.3), удовлетворяющее условию (П.5), при котором линейная функция (П.4) принимает оптимальное (максимальное или минимальное) значение.

В рассматриваемой задаче все неравенства вида “ £ “, хотя могут быть и вида “³“, каждое такое неравенство, как мы видели на примерах, определяет полупространство в n -мерном пространстве. Постоянные коэффициенты a_ij являются, как правило, нормами расхода i-го ресурса на производство единицы j- го изделия (продукта). Коэффициенты b_i задают предельные объемы использования i -го ресурса. Коэффициенты c_j определяют удельную прибыль (или затраты) от производства единицы j -го изделия (продукта).

Если мы какую-либо производственную задачу смоделировали в виде задачи линейного программирования, то в ходе ее решения можно получить следующие результаты:

1.Ограничения могут оказаться несовместными, и задача не имеет решения.

1. Целевая функция не ограничена в области допустимых планов, ее максимум (или минимум) ® + ¥ (- ¥).

2. Оптимальное решение единственное (целевая функция касается области допустимых планов в единственной вершине, ее координаты и определяют оптимальный план).

3. Существует некоторое множество оптимальных решений (планов).

Если задача экономически поставлена правильно, то 1-й и 2-ой случаи исключаются.

Поиск по сайту: