Проверка коэффициента корреляции на существенность

На практике оценка связи между какими-либо показателями, как правило, осуществляется на небольшом объеме наблюдения. Такой объем наблюдения можно рассматривать как выборку. Поэтому коэффициент корреляции, рассчитанный по выборке, может не отражать истинного значения связи, которое имеет место в генеральной совокупности, и будет иметь случайное значение. Это вызывает необходимость в проверке коэффициента корреляции на его существенность (значимость).

Перед последующей проверкой полученного коэффициента корреляции необходимо, чтобы соблюдались следующие условия:

а) выборочная совокупность должна быть получена из генеральной совокупности, имеющей нормальное или близкое к нормальному распределение;

б) объем выборки должен быть меньше 30. Если объем выборки более 50, то последующие расчеты ведутся по-другому.

Проверка полученного коэффициента корреляции на его существенность (значимость) основана на проверке нулевой гипотезы о том, что коэффициент корреляции в генеральной совокупности равен нулю или что между исследуемыми показателями нет связи, т.е. .

Вначале проверки определяется расчетное значение случайной величины по распределению Стъюдента

, (9.2)

где n – число вариантов показателей.

Затем определяется табличное значение случайной величины по распределению Стъюдента . Для этого исследователем задается уровень значимости а, рассчитывается доверительная вероятность γ=1– а и определяется число степеней свободы k=n – 2. На основе γ и k по таблице (приложение 3) находится .После этого сравниваются расчетное и табличное значения.

Если 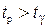, то нулевая гипотеза отвергается, коэффициент корреляции считается существенным и между показателями существует связь.

Если 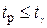, то нулевая гипотеза принимается, коэффициент корреляции считается несущественным, а между показателями отсутствует связь.

По рассмотренному алгоритму осуществим проверку коэффициента корреляции, который рассчитывался с целью оценки тесноты связи между затратами на рекламу и товарооборотом.

Вначале по формуле (9.2) рассчитаем

.

Затем зададимся уровнем значимости . Напомним, что уровень значимости может быть любой, но, как правило, выбирается указанный выше. Тогда доверительная вероятность γ=1– а =1–0,05=0,95.

Определим число степеней свободы k=n – 2 =10–2=8. На основе рассчитанных γ и k в приложении 3 найдем табличное значение; . Если сравним между собой полученные значения и , то получим, что , так как 8,68 > 2,306. Результаты сравнения позволяют сделать вывод: с вероятностью 0,95 нулевая гипотеза может быть отвергнута, коэффициент корреляции можно считать существенным и между показателями существует связь.

Поиск по сайту: