Оценка уравнения регрессии

После того как была выбрана модель уравнения регрессии и рассчитаны ее параметры, наступает этап оценки их существенности (значимости). Это обусловлено тем, что уравнение регрессии мы рассчитали по данным выборки. А это может привести к тому, что значения полученных параметров уравнения регрессии могут быть случайными и не будут соответствовать значениям параметров уравнения регрессии в генеральной совокупности.

Для проверки существенности полученных параметров, при объеме выборки не более 30, используется распределение Стъюдента. Вначале выдвигается нулевая гипотеза о том, что полученные параметры случайны и не отражают истинных значений в генеральной совокупности. Для этого по каждому параметру уравнения регрессии вычисляется расчетное значение случайной величины по распределению Стъюдента .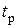

Для параметра 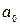расчетное значение случайной величины будет равно

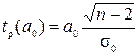, (9.9)

где 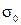– остаточное среднее квадратическое отклонение зависимого показателя.

Остаточная дисперсия отражает вариацию зависимого показателя, обусловленную действием факторов, которые не были учтены в уравнении регрессии. Она может быть определена следующим образом:

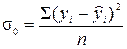, (9.10)

или 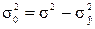. (9.11)

Отсюда остаточное среднее квадратическое отклонение

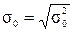. (9.12)

Для параметра 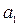расчетное значение случайной величины

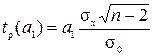, (9.13)

где 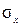– среднее квадратическое отклонение фактора;

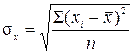. (9.14)

Затем определяется табличное значение случайной величины t _γ по распределению Стъюдента. Для этого исследователем задается уровень значимости а, рассчитывается доверительная вероятность γ=1– а и определяется число степеней свободы k=n – 2. На основе γ и k в приложении 3 находится табличное значение t _γ.

На следующем этапе сравниваются значения расчетное 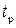и табличное t _γ.

Если t _p> t _γ, то нулевая гипотеза отвергается, параметры считаются значимыми и отражают истинные значения в генеральной совокупности.

Если t _p≤ t _γ, то нулевая гипотеза принимается, параметры считаются случайными и не отражают истинных значений в генеральной совокупности.

Пример 9.4 Проверим значимость параметров уравнения регрессии, описывающего связь затрат на рекламу с товарооборотом .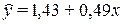

Выдвинем следующую нулевую гипотезу: полученные параметры случайны и не отражают истинных значений параметров в генеральной совокупности.

Для проверки выдвинутой гипотезы рассчитаем t _p для каждого параметра в отдельности и сопоставим их с табличным t _γ. Расчеты проведем в табл. 9.8 на основе данных граф 2,3,4 табл.9.7.

Таблица 9.8

№ п/п
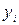
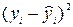
		2,3 3,5 4,5 4,5 4,3 5,8 7,2	1,92 2,41 2,9 3,39 3,88 4,37 4,86 5,35 5,84 6,33	0,06 0,01 0,36 0,15 0,01 0,02 0,13 1,1 0,002 0,45	20,25 12,25 6,25 2,25 0,25 0,25 2,25 6,25 12,25 20,25
Итого		41,1	–	2,29	82,5

Определим значения графы 5:

для первой сроки 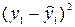=(2−1,92)²=0,06,

для второй строки 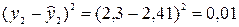и т.д.

Теперь по итогу графы 5 определим остаточное среднее квадратическое отклонение товарооборота

.

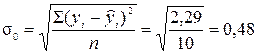Для заполнения графы 6 предварительно определим среднее значение фактора на основе итога графы 2. Среднее значение фактора

.

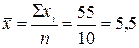Зная среднее значение фактора, определим значения графы 6: для первой строки 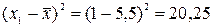, для второй строки 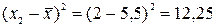и т.д. По итогу графы 6 определим среднее квадратическое отклонение фактора

σ _x .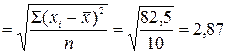

Найдя все необходимые промежуточные значения, определим теперь расчетное значение t _p:

для параметра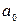

;

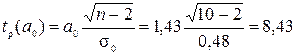для параметра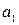

.

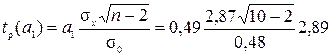Затем определим табличное значение случайной величины t _γ по распределению Стъюдента. Для этого исследователем задается уровень значимости а, рассчитывается доверительная вероятность γ=1– а и определяется число степеней свободы k=n – 2. На основе γ и k в приложении 3 находится табличное значение t _γ. Оно равно 2,306 (порядок расчета приведен в конце раздела 9.3). Сопоставив полученные расчетные значения t _p с табличным t _γ, мы видим, что для каждого параметра выполняется условие t _p> t _γ. А это означает, что нулевая гипотеза отвергается, параметры считаются значимыми и отражают истинные значения в генеральной совокупности.

Поиск по сайту: