Регрессионный анализ связей

Рассмотренный выше корреляционный анализ был основан на эмпирических данных. Такой подход к изучению связей между показателями не всегда дает качественный результат, поскольку эмпирическая линия регрессии отражает как функциональный (детерминированный), так и случайный характер связей по факту. Кроме того, нельзя будет рассчитать промежуточные или прогнозные значения зависимого показателя.

Чтобы выполнить этот и другие расчеты, необходимо описать корреляционную связь показателей в аналитической форме. Для этого могут быть использованы следующие уравнения регрессии (модели):

а) линейная ;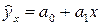

б) парабола второго порядка ;

в) показательная ;

г) степенная и другие,

где х – фактор;

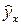– зависимый показатель;

– параметры уравнения регрессии;

– коэффициенты уравнения регрессии.

Для нахождения параметров, например, линейного уравнения регрессии может быть использован метод наименьших квадратов (МНК). На основе МНК строится система линейных уравнений

(9.3)

где n − число вариантов показателей.

Таблица 9.5

№ п/п
i n
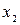
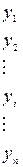
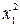
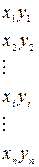
Итого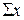

Для проведения промежуточных расчетов при нахождении параметров линейного уравнения регрессии используется табл.9.5.

Решив систему линейных уравнений, найдем параметры:

; (9.4)

. (9.5)

Пример 9.2. Опишем регрессионную связь между затратами на рекламу и товарооборотом с помощью линейного уравнения регрессии 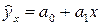. Для нахождения параметров уравнения используем данные граф 2,3 табл.9.3. А все необходимые промежуточные расчеты проведем в табл. 9.6, по итоговым данным которой и найдем параметры уравнения регрессии, используя формулы (9.4) и (9.5).

Таблица 9.6

№ п/п
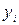
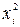
		2,3 3,5 4,5 4,5 4,3 5,8 7,2		4,6 10,5 31,5 34,4 52,2
Итого		41,1		266,2

;

.

В результате расчетов параметров уравнение регрессии будет иметь следующий вид: . Анализ параметров уравнения регрессии показывает, что с ростом на единицу затрат на рекламу объем товарооборота увеличится в среднем на 0,49 единицы объема товарооборота.

Если для описания корреляционной связи выбраны нелинейные модели (например, степенная, показательная, гипербола), то, чтобы найти параметры с помощью метода МНК, эти модели необходимо предварительно линеаризировать. Например, пусть выбрана показательная модель 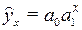. Для нахождения параметров прологарифмируем ее и получим . Теперь уже с помощью МНК можно найти параметры линеаризированной модели. Промежуточные расчеты целесообразно проводить в табличной форме (см. табл.9.6) Однако в расчете будет участвовать уже не y, а lg y. С учетом этого по формулам (9.4) и (9.5) мы найдем не , а их логарифмы – . После того как мы их пропотенцируем, найдем требуемые значения , которые необходимо будет вставить в модель.

Следует отметить, что одна и та же связь между показателями может быть описана несколькими моделями, которые будут иметь разную степень аппроксимации (приближения) к исходным данным. Поэтому, чтобы выбрать оптимальную модель с позиции аппроксимации, вначале на основе здравого смысла нужно выбрать несколько типов моделей, потом рассчитать их параметры и сравнить эти модели между собой. Для выбора оптимальной модели по степени аппроксимации можно использовать критерий наименьшей суммы квадратов отклонений . Та модель, у которой этот критерий будет наименьшим, будет наилучшим образом аппроксимирована к исходным данным. Этот прием выбора наилучшей регрессионной модели является наиболее простым и может быть использован при расчете вручную.

Если использовать Excel или статистические программы, то они не только автоматически рассчитают параметры выбранного уравнения регрессии, но и определят коэффициент детерминации R². Последний можно рассматривать как оценку степени аппроксимации выбранного уравнения регрессии к исходным данным или как меру тесноты связи между фактором и зависимым показателем. В учебной литературе его еще называют теоретическим коэффициентом детерминации и обозначают η ². Он изменяется в интервале [0, 1].

Коэффициент детерминации

; (9.6)

где −общая дисперсия зависимого показателя;

– факторная дисперсия зависимого показателя;

– среднее значение зависимого показателя, рассчитанное по фактическим данным;

y_i – i -е значение зависимого показателя по фактическим данным;

– i -е значение зависимого показателя по уравнению регрессии.

Общая дисперсия отражает изменение (вариацию) зависимого показателя под действием множества различных факторов, в том числе и фактора, который был учтен в уравнении регрессии

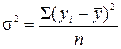, (9.7)

где n – число вариантов показателей.

Факторная дисперсия отражает вариацию зависимого показателя под действие фактора, учтенного в уравнении регрессии. Формула (9.6) позволяет также интерпретировать коэффициент детерминации как долю вариации зависимого показателя, обусловленную действием фактора, учтенного в уравнении регрессии.

Факторную дисперсию можно определить следующим образом

. (9.8)

Пример 9.3 С помощью табл.9.7 проведем расчет коэффициента детерминации для рассчитанного выше уравнения регрессии, использовав данные граф 2,3 табл.9.6.

Вначале по данным графы 3 определим среднее значение зависимого показателя

.

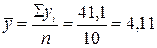Таблица 9.7

№ п/п
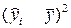
		2,3 3,5 4,5 4,5 4,3 5,8 7,2	1,92 2,41 2,9 3,39 3,88 4,37 4,86 5,35 5,84 6,33	4,45 3,28 0,37 1,23 0,01 0,15 0,15 0,04 2,86 9,55	4,8 2,89 1,46 0,52 0,05 0,07 0,56 1,54 2,99 4,93
Итого	–	41,1	–	22,09	19,81

Затем в графе 4 определим значения зависимого показателя по рассчитанному уравнению регрессии .

Для этого в уравнение будем последовательно подставлять значения х из графы 2. Так, для первой строки графы 4 зависимый показатель по уравнению

регрессии

, для второй строки графы 4 и т. д.

На следующем шаге определим значения показателя графы 5, используя данные графы 3 и среднее значение зависимого показателя (4,11). Так, для первой строки , для второй строки и т.д.

Теперь заполним графу 6 по данным графы 4 и среднему значению зависимого показателя (4,11). Так, для первой строки , для второй строки и т.д.

В заключении определим коэффициент детерминации по формуле (9.6)

.

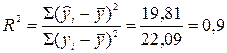Он показывает, что между затратами на рекламу и товарооборотом существует тесная связь, а доля вариации товарооборота, обусловленная фактором затрат на рекламу, составляет 90%. Если мы рассчитаем коэффициент детерминации для другого уравнения регрессии (например, для показательного уравнения регрессии), то после сопоставления коэффициентов можем определить, какая из выбранных моделей наилучшим образом аппроксимирована к исходным данным.

Поиск по сайту: