АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Связи экономических показателей: понятие, формы, виды

Читайте также:
  1. III. Реклама и связи с общественностью в коммерческой сфере.
  2. Авторское право: понятие, объекты и субъекты
  3. Активные операции коммерческих банков: понятие, значение, характеристика видов
  4. Акты применения права: понятие, особенности и виды.
  5. Акты применения права: понятие, признаки, виды
  6. Акты толкования права: понятие, особенности, виды.
  7. Анализ взаимосвязи двух временных рядов
  8. Анализ взаимосвязи между обобщающими, частными показателями экономической эффективности деятельности предприятия и эффективностью каждого научно-технического мероприятия
  9. Анализ функциональной связи между затратами, объемом продаж и прибылью. Определение безубыточного объема продаж и зоны безопасности предприятия
  10. Анализ функциональной связи между издержками и объемом производства продукции
  11. Анализ эколого-экономических систем
  12. Аппаратура линии связи: аппаратура передачи данных, оконечное оборудование, промежуточная аппаратура.

Тема 9. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

 

 

Связи экономических показателей: понятие, формы, виды

 

В экономике многие экономические показатели связаны между собой. Это приводит к тому, что изменение одного показателя вызывает определенное изменение другого. Сама взаимосвязь экономических показателей может быть как непосредственной, так и опосредованной. Так, например, общий расход какого-либо ресурса на выпуск конкретного товара непосредственно (напрямую) зависит от количества произведенного товара при неизменности нормы расхода ресурса. А вот связь затрат на рекламу с объемом реализации товара на рынке является опосредованной, так как реклама воздействует на покупателя, а покупатель уже с определенной вероятностью может увеличить потребление рекламируемого товара.

Изучение связей экономических показателей между собой является одной из центральных задач статистики. Основным условием выявления связей между показателями является проведение массового наблюдения, а не наличие единичного факта.

При решении отмеченной задачи вначале определим показатель, значение которого может изменяется в результате связей с другими показателями. Такой показатель будем называть зависимым (результативным) показателем и обозначать 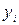. Затем выберем такие показатели, изменение которых может вызвать определенное изменение зависимого показателя. Эти показатели будем называть независимыми показателями, или факторами, и обозначать . Следует отметить, что факторы могут взаимодействовать как с зависимым от них показателем, так и между собой. Например, себестоимость произведенной продукции (зависимый показатель) напрямую зависит как от цен использованных ресурсов, так и норм расхода определенного ресурса.

Связям экономических показателей присущи две крайние формы: функциональная и случайная.

Функциональная (детерминированная) связьфакторов и зависимого показателя – это такая их связь, при которой любому значению фактора соответствует одно (в крайнем случае два) значение (значения) зависимого показателя. Такую связь можно описать с помощью определенной функции

.

Графически функциональная связь может быть выражена в виде прямой, кривой (парабола, гипербола, экспонента и т.д.). Например, заработок (зависимый показатель) рабочего-сдельщика напрямую зависит от числа изготовленных им деталей (фактор), при неизменности расценки за единицу изготовленной детали . Отмеченную связь показателей можно выразить с помощью следующей функции , отражающей линейную связь заработка и количества изготовленных деталей. На графике она имеет вид прямой (рис.9.1). Количественно функциональная связь может быть оценена единицей.

 
Случайная связь факторов и зависимого показателя – это такая их связь, при которой любому значению фактора соответствует множество значений зависимого показателя, распределенных по определенному закону с постоянным значением математического ожидания и дисперсии, т.е. . В этом случае можно считать, что между факторами и зависимым показателем нет связи и количественно она может быть оценена нулем. Случайная связь (рис. 9.2) показывает, что точки (конкретное значение связи) случайным образом расположены относительно некой средней линии (пунктирная линия), соответствующей значению математического ожидания.

Промежуточное положение между крайними формами связей факторов и зависимого показателя занимает корреляционная связь. Корреляционная связьфакторов и зависимого показателя, – это такая их связь, при которой любому значению фактора соответствует несколько значений зависимого показателя, обусловленные действием функциональной и случайной связей. При этом с изменением фактора изменяется в среднем и зависимый показатель. Такое изменение зависимого показателя можно рассматривать как некую тенденцию его развития.

Корреляционная связь (рис.9.3) показывает, что с ростом значений фактора в среднем возрастает значение зависимого показателя . На графике среднее изменение зависимого показателя отображено пунктирной линией. Для изучения корреляционной связи в статистике используется корреляционно-регрессионный анализ. Корреляционный анализ направлен на выявление и оценку тесноты связи между факторами и зависимым показателем, а регрессионный анализ − на выявление и оценку формы корреляционной связи.

В зависимости от числа факторов различают парную корреляционную связь, когда используется зависимый показатель и один фактор, и множественную, когда используется несколько факторов.

Корреляционная связь может быть прямой и обратной, линейной и нелинейной. Прямая корреляционная связь между фактором и зависимым показателем – это такая их связь, при которой с ростом фактора растет в среднем и зависимый показатель (рис.9.3). Обратнаякорреляционная связь между фактором и зависимым показателем – это такая их связь, при которой с ростом фактора зависимый показатель в среднем убывает. Линейная корреляционная связь между фактором и зависимым показателем – это такая их связь, при которой с изменением фактора в среднем линейно изменяется и зависимый показатель (рис.9.3). Нелинейная корреляционная связь между фактором и зависимым показателем – это такая их связь, при которой с изменением фактора в среднем нелинейно изменяется и зависимый показатель. При нелинейной связи зависимый показатель может изменяться в среднем по параболе, гиперболе, экспоненте и т.д.

Исходя из содержания анализируемого экономического процесса факторы и зависимый показатель могут быть как количественными, так и качественными. Количественные показатели анализируются с помощью корреляционно-регрессионного анализа. Для этого используются графический метод, методы аналитических группировок регрессионного моделирования и т.д.

Для изучения связей между качественными показателями могут быть использованы коэффициенты корреляции рангов Спирмена или Кендэла.

 


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)