 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Учет инфляционного обесценения денег в принятии финансовых решений
Пусть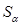 
- сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы S при отсутствии инфляции. Через 
обозначим разницу между этими суммами.
Отношение / S, выраженное в процентах, называется уровнем инфляции. При расчетах используют относительную величину уровня инфляции - темп инфляции 
.
Тогда для определения 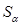получаем следующее выражение:
.
Величину 
, показывающую, во сколько раз 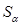больше S (т. е. во сколько раз в среднем выросли цены), называют индексом инфляции 
.
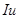Пусть - годовой уровень инфляции. Это значит, что через год сумма 
будет больше суммы S в (1 + .) раз. По прошествии еще одного года сумма 
будет больше суммы в (1 + ) раз, т. е. больше суммы S в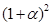 
раз. Через п лет сумма 
вырастет по отношению к сумме S в 
раз. Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции . - тоже самое, что наращение суммы S по сложной годовой ставке процентов .
Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.).
Если известен годовой уровень инфляции ., то за период в п лет (при том, чтo 
и 
- целое число лет, 
- оставшаяся нецелая часть года) индекс инфляции, очевидно, составит следующую величину: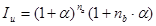 
В некоторых случаях может быть задан уровень инфляции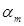 
за короткий (меньше года) интервал. Тогда за период, составляющий т таких интервалов, индекс инфляции будет равен: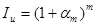 
Теперь можно приложить изложенные выше варианты начисления процентов к условиям инфляционной экономики.
Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму 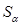, что требует уже иной процентной ставки.
Назовем ее ставкой процентов, учитывающей инфляцию.
Пусть: 
- простая ставка ссудного процента, учитывающая инфляцию; 
- простая учетная ставка, учитывающая инфляцию; 
- сложная ставка ссудного процента, учитывающая инфляцию; 
- сложная учетная ставка, учитывающая инфляцию; 
номинальная ставка сложного процента, учитывающая инфляцию; 
- номинальная сложная учетная ставка, учитывающая инфляцию.
Зададим годовой уровень инфляции и простую годовую ставку ссудного процента i Тогда для наращенной суммы S, превращающейся в условиях инфляции в сумму 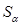, используем формулу: 
.
Для данной суммы можно записать еще одно соотношение: 
а затем составить уравнение эквивалентности: 
из которого следует, что 
Мы получили, таким образом, известную формулу И. Фишера, в которой сумма 
является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь эта величина называется инфляционной премией.
Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период. Для простых ссудных процентных ставок получаем: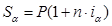 
в то же время должно выполняться равенство: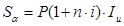 
Составим уравнение эквивалентности: 
из которого получаем: 
Для простых учетных ставок аналогичное уравнение эквивалентности будет иметь вид:
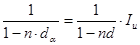, откуда 
Для случая сложных ссудных процентов используем формулы:
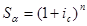
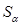
Отсюда 
Если начисление процентов происходит несколько (m) раз в году, используется следующая формула:
,
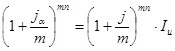Отсюда 
Таким же образом получаем две формулы для случаев сложных учетных ставок:
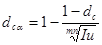
Используя полученные Формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течение рассматриваемого периода. Эти формулы можно преобразовать и получить зависимость i от или любую другую. Например, из формулы можно получить формулу, позволяющую определить реальную доходность финансовой операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию:
Из Формулы - получаем аналогичную формулу для случая сложных процентов:
Подставив в последнюю формулу вместо индекса инфляции выражение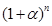 
, получим простую формулу: 
отражающую несколько очевидных соображений: если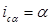 
(доходность вложений и уровень инфляции равны), то 
, т. е. весь доход поглощается инфляцией; если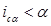 
(доходность вложений ниже уровня инфляции), то 
, то есть операция приносит убыток; если 
(доходность вложений выше уровня инфляции), то 
, т.е. происходит реальный прирост вложенного капитала.
Вопросы для самоконтроля:
Какие способы начисления процентов вы знаете и в чем их сущность.
Дайте определение следующим понятиям: временной стоимости денег, настоящая и будущая стоимость капитала, дисконтирование и компаундирование, простые и сложные ставки ссудных процентов, простые и сложные учетные ставки, эквивалентность процентных ставок различного типа, аннуитеты, чистая приведенная стоимость, амортизация долга.
Как учитывается инфляция в принятии финансовых решений.
Как определить доходность операций с ценными бумагами.
Как определить возврат основной суммы долга и процентов?
Поиск по сайту: