 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Равномерное движение
1.Мао В. Современная криптография: теория и практика.: Пер. с англ. – М.: изд. дом «Вильямс», 2005. –768с.:ил.
2.Масленников М. Практическая криптография. –СПб.: БХВ-Петербург, 2003.—464с.:ил.
3 Нечаев В. Элементы криптографии. Основы теории защиты информации: Учеб. пособие для вузов / Под ред. В.А. Садовничего.– 2-е изд стер. – М.: Высш.шк., 2004. – 424с.
4 Яблонский С. Введение в дискретную математику: Учеб. пособие для вузов / Под ред. В.А. Садовничего.– 3-е изд стер. – М.: Высш.шк., 2002. –384с.
5.Андерсон Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.: изд. дом «Вильямс», 2004. –960с.:ил.
Теория алгоритмов:: Методические указания для самостоятельной подготовки к контролю знаний студентов заочного отделения направления подготовки 6.050101 «Компьютерные науки» / Сост. М.П.Богдан. – Краматорск: ДГМА, 2012. – 36 с.
Автор: Михаил Петрович Богдан,
Редактор саморедактирование
----------------------------------------------------------------------------------
ДДМА. 84313, Краматорськ, вул. Шкадінова, 72
Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени радиус-вектора  (векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).

|
Рисунок 1.1.1.
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус–вектора  . .  – радиус–вектор положения точки в начальный момент времени. – радиус–вектор положения точки в начальный момент времени.
|
Перемещением тела  называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
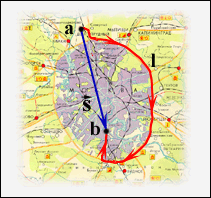
В случае достаточно малого промежутка времени Δ t пройденный телом путь Δ l почти совпадает с модулем вектора перемещения  При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
|
Рисунок 1.1.2.
Пройденный путь l и вектор перемещения  при криволинейном движении тела. a и b – начальная и конечная точки пути. при криволинейном движении тела. a и b – начальная и конечная точки пути.
|
Для характеристики движения вводится понятие средней скорости:

|
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δ t:
|
В математике такой предел называют производной и обозначают  или
или 
Мгновенная скорость  тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

|
Рисунок 1.1.3.
Средняя и мгновенная скорости. 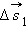 , ,  , ,  – перемещения за времена – перемещения за времена  соответственно. При t → 0 соответственно. При t → 0 
|
При движении тела по криволинейной траектории его скорость  изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости  за некоторый малый промежуток времени Δ t можно задать с помощью вектора
за некоторый малый промежуток времени Δ t можно задать с помощью вектора  (рис. 1.1.4).
(рис. 1.1.4).
Вектор изменения скорости  за малое время Δ t можно разложить на две составляющие:
за малое время Δ t можно разложить на две составляющие:  направленную вдоль вектора
направленную вдоль вектора  (касательная составляющая), и
(касательная составляющая), и  направленную перпендикулярно вектору
направленную перпендикулярно вектору  (нормальная составляющая).
(нормальная составляющая).

|
Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению.  – изменение вектора скорости за время – изменение вектора скорости за время  . .
|
Мгновенным ускорением (или просто ускорением)  тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости  к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
|
Направление вектора ускорения  в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 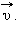 Составляющие вектора ускорения
Составляющие вектора ускорения  называют касательным (тангенциальным)
называют касательным (тангенциальным)  и нормальным
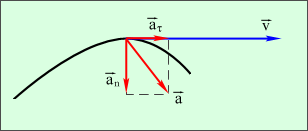
и нормальным  ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).
|
| Рисунок 1.1.5. Касательное и нормальное ускорения. |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

|
Вектор  направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

|
| Рисунок 1.1.6. Движение по дугам окружностей. |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:

|
Вектор  всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
Из рис. 1.1.5 видно, что модуль полного ускорения равен

|
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение  , скорость
, скорость  и ускорение
и ускорение  . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение  , скорость
, скорость  и ускорение
и ускорение  – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени радиус-вектора  (векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
(векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).

|
Рисунок 1.1.1.
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус–вектора  . .  – радиус–вектор положения точки в начальный момент времени. – радиус–вектор положения точки в начальный момент времени.
|
Перемещением тела  называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δ t пройденный телом путь Δ l почти совпадает с модулем вектора перемещения  При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

|
Рисунок 1.1.2.
Пройденный путь l и вектор перемещения  при криволинейном движении тела. a и b – начальная и конечная точки пути. при криволинейном движении тела. a и b – начальная и конечная точки пути.
|
Для характеристики движения вводится понятие средней скорости:

|
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δ t:
|
В математике такой предел называют производной и обозначают  или
или 
Мгновенная скорость  тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

|
Рисунок 1.1.3.
Средняя и мгновенная скорости. 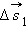 , ,  , ,  – перемещения за времена – перемещения за времена  соответственно. При t → 0 соответственно. При t → 0 
|
При движении тела по криволинейной траектории его скорость  изменяется по модулю и направлению. Изменение вектора скорости
изменяется по модулю и направлению. Изменение вектора скорости  за некоторый малый промежуток времени Δ t можно задать с помощью вектора
за некоторый малый промежуток времени Δ t можно задать с помощью вектора  (рис. 1.1.4).
(рис. 1.1.4).
Вектор изменения скорости  за малое время Δ t можно разложить на две составляющие:
за малое время Δ t можно разложить на две составляющие:  направленную вдоль вектора
направленную вдоль вектора  (касательная составляющая), и
(касательная составляющая), и  направленную перпендикулярно вектору
направленную перпендикулярно вектору  (нормальная составляющая).
(нормальная составляющая).

|
Рисунок 1.1.4.
Изменение вектора скорости по величине и направлению.  – изменение вектора скорости за время – изменение вектора скорости за время  . .
|
Мгновенным ускорением (или просто ускорением)  тела называют предел отношения малого изменения скорости
тела называют предел отношения малого изменения скорости  к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
к малому промежутку времени Δ t, в течение которого происходило изменение скорости:
|
Направление вектора ускорения  в случае криволинейного движения не совпадает с направлением вектора скорости
в случае криволинейного движения не совпадает с направлением вектора скорости 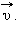 Составляющие вектора ускорения
Составляющие вектора ускорения  называют касательным (тангенциальным)
называют касательным (тангенциальным)  и нормальным
и нормальным  ускорениями (рис. 1.1.5).
ускорениями (рис. 1.1.5).

|
| Рисунок 1.1.5. Касательное и нормальное ускорения. |
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

|
Вектор  направлен по касательной к траектории.
направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

|
| Рисунок 1.1.6. Движение по дугам окружностей. |
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:

|
Вектор  всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
Из рис. 1.1.5 видно, что модуль полного ускорения равен

|
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение  , скорость
, скорость  и ускорение
и ускорение  . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение  , скорость
, скорость  и ускорение
и ускорение  – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
– величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Следует обратить внимание на вопрос об ускорениях тела в различных системах отсчета. Из (*) следует, что при равномерном и прямолинейном движении систем отсчета друг относительно друга ускорения тела в этих двух системах одинаковы, т. е.  Действительно, если
Действительно, если 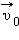 – вектор, модуль и направление которого остаются неизменными во времени, то любое изменение
– вектор, модуль и направление которого остаются неизменными во времени, то любое изменение 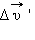 относительной скорости тела будет совпадать с изменением
относительной скорости тела будет совпадать с изменением  его абсолютной скорости. Следовательно,
его абсолютной скорости. Следовательно,
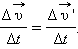
|
Переходя к пределу (Δ t → 0), получим 
В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными.
В случае, когда вектора относительной скорости  и переносной скорости
и переносной скорости 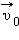 параллельны друг другу, закон сложения скоростей можно записать в скалярной форме:
параллельны друг другу, закон сложения скоростей можно записать в скалярной форме:
| υ = υ0 + υ '. |
В этом случае все движения происходят вдоль одной прямой линии (например, оси OX). Скорости υ, υ0 и υ ' нужно рассматривать как проекции абсолютной, переносной и относительной скоростей на ось OX. Они являются величинами алгебраическими и, следовательно, им нужно приписывать определенные знаки (плюс или минус) в зависимости от направления движения.
Равномерное движение
Простейшим видом механического движения является движение тела вдоль прямой линии с с постоянной по модулю и направлению скоростью. Такое движение называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроектировать на ось OX и рассматривать их проекции как алгебраические величины.
Если в некоторый момент времени t 1 тело находилось в точке с координатой x 1, а в более поздний момент t 2 – в точке с координатой x 2, то проекция перемещения Δ s на ось OX за время Δ t = t 2 – t 1 равна
| Δ s = x 2 – x 1. |
Эта величина может быть и положительной и отрицательной в зависимости от направления, в котором двигалось тело. При равномерном движении вдоль прямой модуль перемещения совпадает с пройденным путем. Скоростью равномерного прямолинейного движения называют отношение

|
Если υ > 0, то тело движется в сторону положительного направления оси OX; при υ < 0 тело движется в противоположном направлении.
Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением:
| x (t) = x 0 + υ t. |
В этом уравнении υ = const – скорость движения тела, x 0 – координата точки, в которой тело находилось в момент времени t = 0. На графике закон движения x (t) изображается прямой линией. Примеры таких графиков представлены на рис. 1.3.1.

|
| Рисунок 1.3.1. Графики равномерного прямолинейного движения. |
Для закона движения, изображенного на графике I (рис. 1.3.1), при t = 0 тело находилось в точке с координатой x 0 = –3. Между моментами времени t 1 = 4 с и t 2 = 6 с тело переместилось от точки x 1 = 3 м до точки x 2 = 6 м. Таким образом, за Δ t = t 2 – t 1 = 2 с тело переместилось на Δ s = x 2 – x 1 = 3 м. Следовательно, скорость тела составляет

|
Величина скорости оказалась положительной. Это означает, что тело двигалось в положительном направлении оси OX. Обратим внимание, что на графике движения скорость тела может быть геометрически определена как отношение сторон BC и AC треугольника ABC (см. рис. 1.3.1)

|
Чем больше угол α, который образует прямая с осью времени, т. е. чем больше наклон графика (крутизна), тем больше скорость тела. Иногда говорят, что скорость тела равна тангенсу угла α наклона прямой x (t). С точки зрения математики это утверждение не вполне корректно, так как стороны BC и AC треугольника ABC имеют разные размерности: сторона BC измеряется в метрах, а сторона AC – в секундах.
Аналогичным образом для движения, изображенного на рис. 1.3.1 прямой II, найдем x 0 = 4 м, υ = –1 м/с.
На рис. 1.3.2 закон движения x (t) тела изображен с помощью отрезков прямых линий. В математике такие графики называются кусочно-линейными. Такое движение тела вдоль прямой не является равномерным. На разных участках этого графика тело движется с различными скоростями, которые также можно определить по наклону соответствующего отрезка к оси времени. В точках излома графика тело мгновенно изменяет свою скорость. На графике (рис. 1.3.2) это происходит в момент времени t 1 = –3 с, t 2 = 4 с, t 3 = 7 с и t 4 = 9 с. Нетрудно найти по графику движения, что на интервале (t 2; t 1) тело двигалось со скоростью υ12 = 1 м/с, на интервале (t 3; t 2) – со скоростью υ23 = –4/3 м/с и на интервале (t 4; t 3) – со скоростью υ34 = 4 м/с.
Следует отметить, что при кусочно-линейном законе прямолинейного движения тела пройденный путь l не совпадает с перемещением s. Например, для закона движения, изображенного на рис. 1.3.2, перемещение тела на интервале времени от 0 с до 7 с равно нулю (s = 0). За это время тело прошло путь l = 8 м.
Поиск по сайту:

