Занятие 1. Тема. Дифференциал функции

Тема. Дифференциал функции. Замена переменной в дифференциале.

Напомним определение дифференциала функции.

Определение 1.1. Если 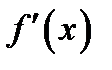есть производная от функции в точке , а произвольное приращение аргумента, то дифференциалом функции назовем произведение . Дифференциал будем обозначать символами . Таким образом

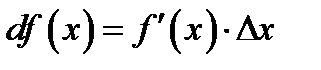(1.1)

Замечание. Если положить , то

Ввиду (1.2) дифференциал от функции будем записывать далее

или (1.2)

Причем точка и величина 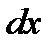не зависят друг от друга и задаются произвольно.

Справедлива формула линейного приближения функции

(1.3)

Отсюда следует, что .

Производную функции можно записывать формулой

(1.4)

Так как дифференциал функции равен произведению производной функции на дифференциал аргумента, то формулы для дифференциалов те же, что и для производных, если каждую умножить на

(1.5)

Таблица дифференциалов аналогична таблице производных.

Таблица дифференциалов

(1.6)

Инвариантность формулы дифференциала

Теорема 1.1. Вид формулы дифференциала функции не изменится, если аргумент функции заменить новой переменной.

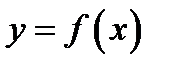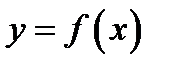Доказательство. Пусть нам дана функция , тогда согласно формуле (1.2) её дифференциал равен , где независимая переменная. Если переменная сама становится зависимой . Тогда функция становится функцией, зависящей от переменной и её дифференциал будет равен .

Применяя цепное правило, получаем

или

(1.7)

Вывод. Для любой переменной 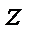формула дифференциала функции справедлива независимо от того является ли переменное независимым или оно есть функция другого независимого переменного.

Поиск по сайту: