АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Замена переменной в дифференциале

Читайте также:
  1. IV. ЕКЗАМЕНАЦІЙНІ БІЛЕТИ
  2. Root(Выражение, имя переменной)
  3. Автоматическая замена шрифта
  4. Вступительного экзамена по педагогике и психологии
  5. Движение тела переменной массы.
  6. Действующее значение периодической несинусоидальной переменной
  7. Динамика переменной массы. Уравнение движения тела переменной массы. Уравнение Циолковского.
  8. Дифференциал независимой переменной
  9. для экзамена по дисциплине «Теория экономического анализа» для студентов специальности «Бухгалтерский учет, анализ и аудит»
  10. ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ № 5
  11. Задание ранжированной переменной
  12. Закон Сох. Импульса. Центр Масс. Уравнение движение тела переменной массы.

Операция замены переменной в дифференциале упрощает выражение дифференциала

Пример 1. В дифференциале 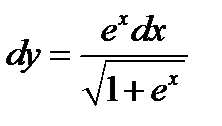заменить переменную по правилу .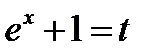

Решение. Из условия задачи следует 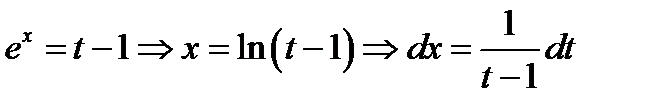. Подставляя полученные данные в дифференциал, получаем ;

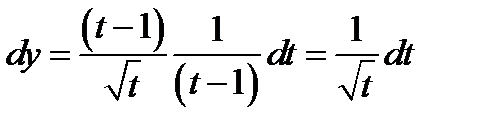Пример 2. В дифференциале 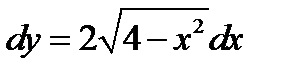заменить переменную по правилу .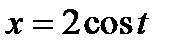

Решение. Из условия задачи следует .

Подставляя полученные данные в дифференциал, получаем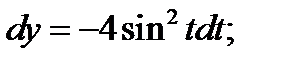

Пример 3. В дифференциале 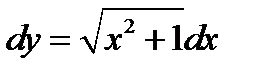заменить переменную по правилу .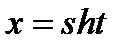

Решение. Из условия задачи следует 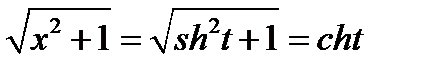; 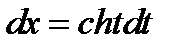. Подставляя полученные данные в дифференциал, получаем ;

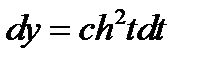Пример 4. В дифференциале 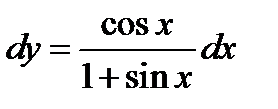заменить переменную по правилу ;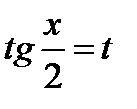

Решение. В данном случае нужно использовать известные тригонометрические формулы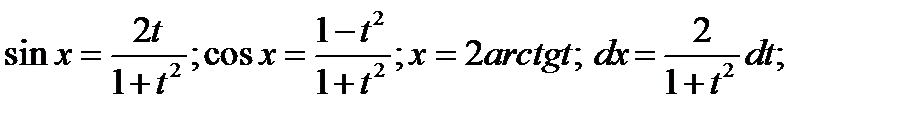

Данная замена переменного называется универсальной тригонометрической подстановкой.

Подставляя полученные данные в дифференциал, получаем

;

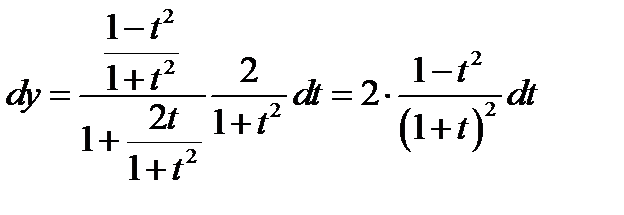Пример 5. В дифференциале 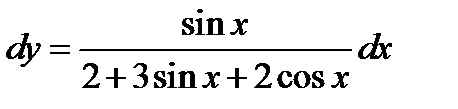заменить переменную по правилу ;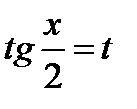

Решение. Применяя универсальную тригонометрическую подстановку, получаем ;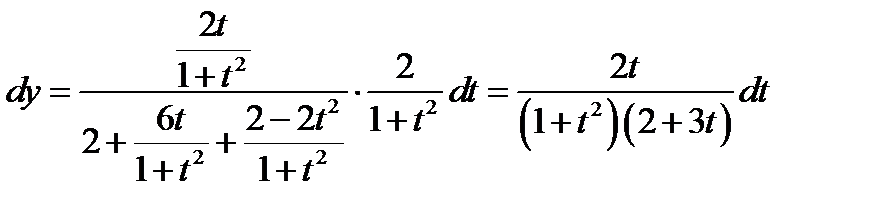

Пример 6. В дифференциале 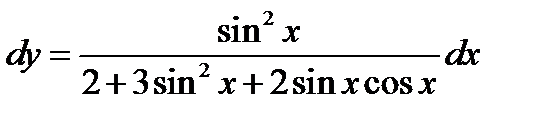заменить переменную по правилу ;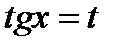

Решение. В данном случае нужно использовать известные тригонометрические формулы

Из условия задачи следует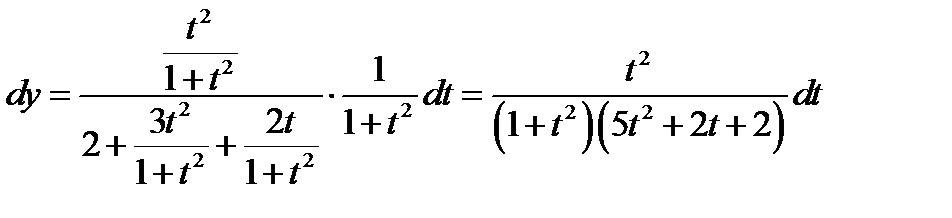

 

Пример 7. В дифференциале заменить переменную по правилу ;

Решение. Из условия задачи следует

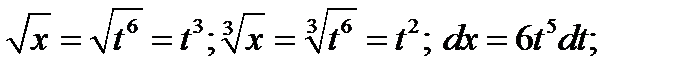
Подставляя полученные данные в дифференциал, получаем ;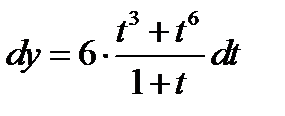

Пример 8. В дифференциале заменить переменную по правилу .

Решение. Из условия задачи следует

Подставляя полученные данные в дифференциал, получаем .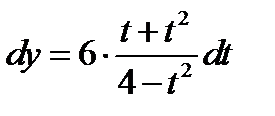

Помимо операции дифференцирования рассмотрим операцию обратную к ней

Пример 9. Рассмотрим следующую задачу. Найти функции, дифференциалы которых равны

следующим выражениям

Решение. 1) Из таблицы дифференциалов (1.6) следует, что .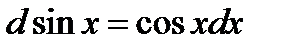

Ответ.

2) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную 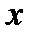по правилу . В результате получаем 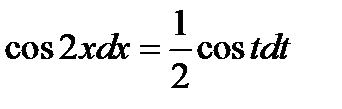. Из таблицы (1.6)

 

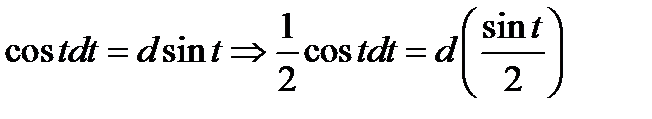. Откуда .

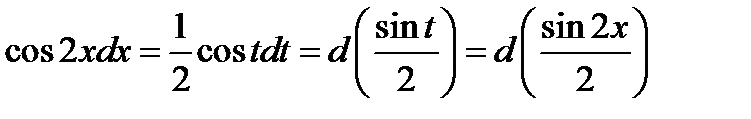Ответ. .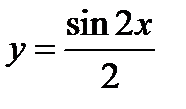

3) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную 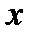по правилу 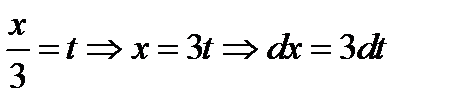. В результате получаем 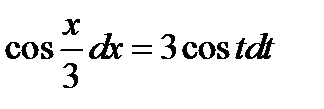. Из таблицы (1.6) . Откуда .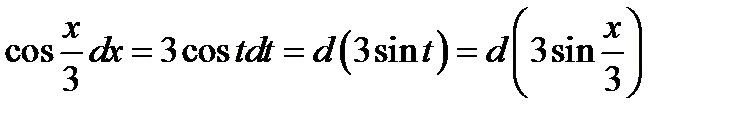

Ответ. .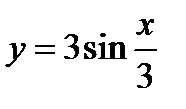

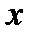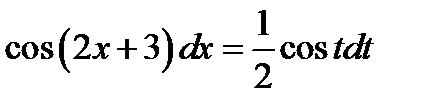4) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную по правилу . В результате получаем . Из таблицы (1.6) . Откуда .

Ответ. .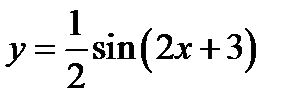

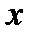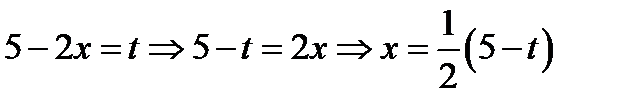
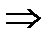
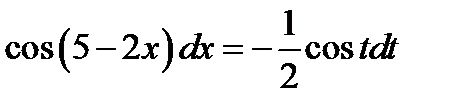5) Сначала мы сведём выражение к табличному дифференциалу. Для этого заменим переменную по правилу . В результате получаем . Из таблицы (1.6) 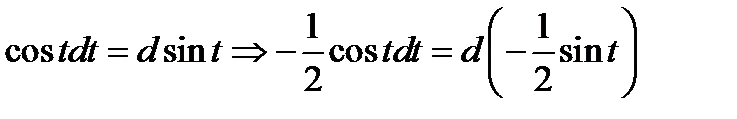. Откуда .

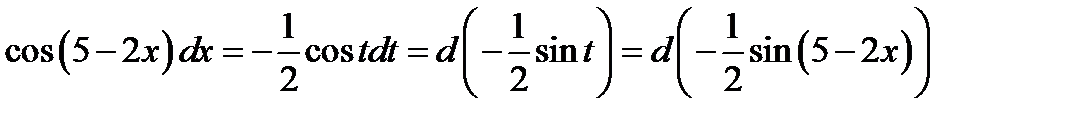Ответ. .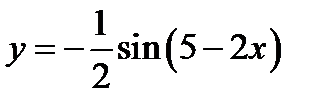

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)