Закон Сох. Импульса. Центр Масс. Уравнение движение тела переменной массы

Импульсом называют векторную величину, равную произведению массы тела на ее скорость:

При взаимодействии тел замкнутой системы полный импульс системы остается неизменным:

Закон сохранения импульса есть следствие второго и третьего законов Ньютона. Пример использования закона сохранения импульса.

Центром масс тела, состоящего из n материальных точек, называется точка (в геометрическом смысле), радиус-вектор которой определяется формулой:

Здесь R1 – радиус-вектор точки с номером i (i = 1, 2,... n).

Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским в 1897 году^[1] для материальной точки переменной массы (состава).

Уравнение обычно записывается в следующем виде:

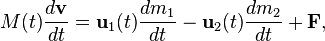
где:

— масса материальной точки, изменяющаяся за счет обмена частицами с окружающей средой, в произвольный момент времени t;

— скорость движения материальной точки переменной массы;

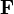— результирующая внешних сил, действующих на материальную точку переменной массы со стороны её внешнего окружения (в том числе, если такое имеет место, и со стороны среды, с которой она обменивается частицами, например электромагнитные силы — в случае массообмена с магнитной средой, сопротивление среды движению и т. п.);

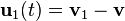— относительная скорость присоединяющихся частиц;

— относительная скорость отделяющихся частиц;

, — скорости массообмена присоединяющихся и отделяющихся частиц.

Формула Циолковского может быть получена как результат решения этого уравнения.

Величина:

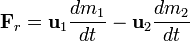
называется «реактивной силой».

Вывод уравнения Мещерского из второго закона Ньютона в форме

где масса материальной точки считается непостоянной,

Поиск по сайту: