Частные производные. Функции двух переменных

Функции двух переменных

Определение. Если каждой паре независимых друг от друга чисел по некоторому правилу ставится в соответствие единственное число z, то говорят, что задана функция двух переменных .

Частные производные

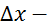приращение переменной x, приращение переменной y.

– полное приращение функции в точке (x, y).

– частное приращение в точке (x, y) по переменной х (y=const).

– частное приращение в точке (x, y) по переменной y (x=const).

Определение. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения к приращению этой переменной при стремлении последнего к нулю.

– частная производная z по x (y=const).

– другое обозначение.

– частная производная z по y (x=const).

– другое обозначение.

Пример. Найти частные производные функции

,

.

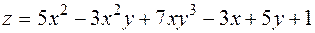
Пример. Найти частные производные функции .

Решение. , .

– полный дифференциал функции .

Пример. Найти полный дифференциал функции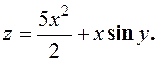

, ,

.

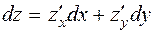Поиск по сайту: