АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Д.у.-2, не содержащие явно искомой функции

Читайте также:
  1. II. Основные задачи и функции
  2. III. Предмет, метод и функции философии.
  3. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  4. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ
  5. А. Средняя квадратическая погрешность функции измеренных величин.
  6. Абстрактные классы и чистые виртуальные функции. Виртуальные деструкторы. Дружественные функции. Дружественные классы.
  7. Адаптивные функции
  8. Администраторы судов, их функции
  9. Алгебраическое интерполирование функции.
  10. Анализ функции логики высказываний
  11. Аналитические функции
  12. Арендная плата: состав и функции

Уравнение вида: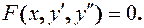

Замена переменной: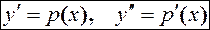

Тогда получаем – д.у.-1.

Пример. Найти общее решение уравнения .

Применяем подстановку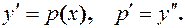

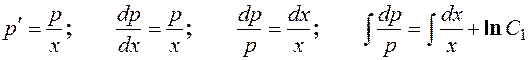
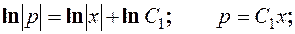
Произведя обратную замену, получаем:

 

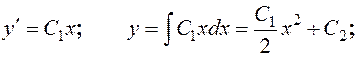
Отметим, что – решение д.у. для всех значений переменной х кроме значения х = 0.

Д.у.-2, не содержащие явно независимой переменной

Это уравнения вида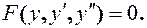

Порядок таких уравнений может быть понижен с помощью замены переменных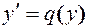

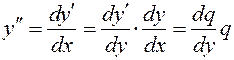
Пример. Найти общее решение уравнения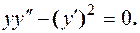

Замена переменной: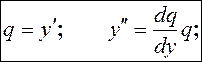

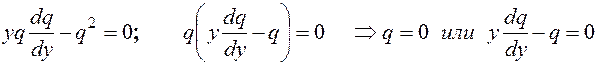
1)

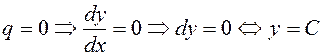
2) .

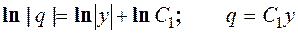
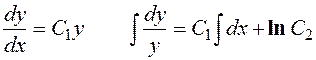
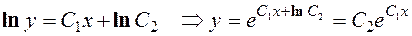
Ответ: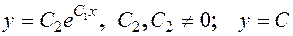


 

Определение типа д.у.-1 и д.у.-2


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)