АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Однородные уравнения. Определение. Функция f(x, y) называется однородной n-го измерения относительно своих аргументов х и у

Читайте также:
  1. VI Дифференциальные уравнения
  2. Алгебраические уравнения
  3. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  4. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  5. Геометрическая оптика.отражение и преломление света. законы отражения и преломления.Зеркала и линзы.Уравнения для зеркал и линз.оптические приборы.
  6. Геометрические преобразования точек и отрезков. Однородные координаты
  7. Геометрический образ уравнения состояния.
  8. Дифференциальные уравнения 1 порядка с разделяющимися переменными
  9. Дифференциальные уравнения движения вязкой жидкости. Граничные условия.
  10. Дифференциальные уравнения и передаточные функции замкнутых систем управления
  11. Дифференциальные уравнения первого порядка с разделяющимися переменными.
  12. Дифференциальные уравнения первого порядка.

Определение. Функция f(x, y) называется однородной n-го измерения относительно своих аргументов х и у, если для любого значения параметра k (кроме нуля) выполняется тождество:

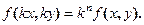
Определение. Д.у. вида 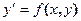называется однородным, если его правая часть есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида 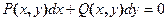является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Метод решения: 1) разделим уравнение на , где n – измерение однородных функций в д.у.

2) замена переменной: Þ получим д.у. с разделяющимися переменными.


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)